РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Гаусса; 2) по формулам Крамера; 3) матричным способом.

ЗАДАНИЕ 1

Решить систему линейных алгебраических уравнений тремя способами: 1) методом Гаусса; 2) по формулам Крамера; 3) матричным способом.

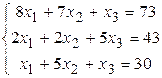
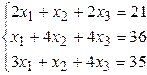
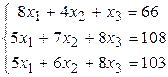
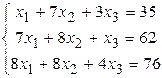
ЗАДАНИЕ 2

Дано: угол между векторами и равен Значения коэффициентов l, m, n, k, f и модули векторов и приведены в табл.

Определите:1)длины диагоналей параллелограмма, построенного на векторах и ;2)угол между диагоналями;3)площадь параллелограмма.

Вариант	p	q	l	m	n	k	f
Вариант	p	q	l	m	n	k	f

 

ЗАДАНИЕ 3

Даны точки А и В. Из точки А выходит луч, направленный по вектору . Найти координаты вектора , который пересекает луч, перпендикулярен ему и равен .

Вари-ант	А	В		Вари-ант	А	В
	(-3;4;2)	(1;12;3)		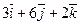	(5;1;-3)	(9;8;1)
	(1;2;-4)	(4;6;8)			(1;2;-1)	(-9;-9;1)
	(-6;5;3)	(-5;7;5)			(5;-3;2)	(8;3;0)
	(2;2;-1)	(8;-4;6)			(-4;9;-7)	(4;-7;4)
	(4;-1;2)	(10;5;9)			(2;2;5)	(1;4;3)
	(-1;-9;2)	(0;9;8)			(8;3;3)	(4;-5;4)
	(-7;-6;3)	(8;4;9)			(-6;7;9)	(6;-2;1)
	(-2;-1;5)	(4;-3;8)			(7;-5;-3)	(-8;1;7)
	(3;-1;4)	(5;1;5)			(-8;2;5)	(6;4;0)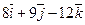
	(1;-1;3)	(5;0;11)			(1;-7;-9)	(2;5;3)
	(3;-1;0)	(9;-3;9)		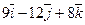	(3;3;1)	(9;-3;8)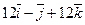
	(-4;1;1)	(3;5;5)			(2;9;6)	(8;-9;5)
	(-5;0;2)	(1;-6;9)			(5;-1;2)	(6;-5;-6)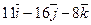
	(-7;5;5)	(5;1;2)			(-7;2;1)	(-9;5;7)
	(1;8;3)	(9;-8;-8)			(3;2;5)	(-1;6;-2)

 

ЗАДАНИЕ 4

Даны координаты вершин пирамиды А₁, А₂, А₃, А_4. Построить пирамиду.

Найти: 1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости грани А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань

А₁А₂А₃.

 

Вариант	А1	А2	А3	А4
	(2; 3; 2)	(10; 7; 3)	(6; 6; 3)	(8; 9; 5)
	(3; 5; 2)	(1; 7; 5)	(5; 6; 8)	(1; 6; 4)
	(6; 1; 4)	(3;-3; 8)	(5;-5; 8)	(8; 3; 3)
	(2; 5; 4)	(5; 3; 6)	(8; 3; 5)	(8; 2; 10)
	(3; 4; 3)	(7;-4; 4)	(6; 0; 4)	(9; 10; 6)
	(1; 2; 3)	(3; 4; 6)	(-3; 1; 6)	(3; 3; 5)
	(3; 5; 1)	(0; 1; 5)	(1; 0; 5)	(7; 9; -1)
	(5;-2; 4)	(7; 1; 6)	(7; 4; 5)	(8; 4; 10)
	(1; 2; 1)	(9;-2; 2)	(-3; 5; 0)	(7; 8;-2)
	(4; 1; 3)	(2; 3; 6)	(5;-3; 6)	(3; 3; 5)
	(3;-1; 2)	(7; 2; 6)	(9; 0; 6)	(5; 1; 3)
	(3; 5; 4)	(1; 8; 6)	(-1; 2; 6)	(9;-1; 1)
	(1; 1; 2)	(-3;9; 3)	(-2; 5; 3)	(7; 7; -1)
	(1; 4; 3)	(-1; 6; 6)	(6; -4; 0)	(2; 2; 1)
	(2; 4; 1)	(6; 7; 5)	(7; 6; 5)	(6; 8; 3)
	(1; 2; 2)	(3; 5; 4)	(5;-1; 4)	(7; 8; 5)
	(2;-2; 1)	(10; 2; 2)	(6; 1; 2)	(8; 4; 4)
	(3; 4;-1)	(1; 6; 2)	(5; 5; 5)	(1; 5; 1)
	(2; 5; 3)	(-1; 1; 7)	(1; -1; 7)	(4; 7; 2)
	(1; 4; 2)	(4; 2; 4)	(7; 2; 3)	(7; 1; 8)
	(3; 1; 4)	(7; -7; 5;)	(6; -3; 5)	(9; 7; 7)
	(2; 4; 3)	(4; 6; 6)	(-2; 3; 6)	(4; 5; 5)
	(5;-2;-1)	(2; -6; 3)	(3; -7; 3)	(9; 2; -3)
	(5; 2; 1)	(7; 5; 3)	(7; 8; 2)	(8; 8; 7)
	(2;-1; 7)	(10;-5; 8)	(-2; 2; 6)	(8; 5; 4)
	(4; 7; 8)	(2; 9; 11)	(5; 3; 11)	(3; 9; 10)
	(2; 1; 3)	(6; 4; 7)	(8; 2; 7)	(4; 3; 4)
	(1; 5; 2)	(-1; 8; 4)	(-3; 2; 4)	(7; -1;-1)
	(6; 1; 4)	(2; 9; 5)	(3; 5; 5)	(12; 7; 1)
	(6; 5; 1)	(4; 7; 4)	(11; -3; -2)	(7; 3;-1)

 

ЗАДАНИЕ 5

 

1. Написать уравнение эллипса, проходящего через точку пересечения гиперболы х² – у² = 2 с прямой х + у – 2 = 0, если известно, что фокусы эллипса совпадают с фокусами гиперболы.

 

2. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом 24х² + 49у² = 1176 при условии, что ее эксцентриситет e = 1,25.

 

3. Написать уравнение окружности такой, чтобы ее диаметром оказался отрезок прямой х + у – 4 = 0, заключенный между осями координат.

 

4. Большая ось эллипса втрое больше его малой оси. Составить каноническое уравнение этого эллипса, если он проходит через точку М(3;Ö3).

 

5. Дана гипербола х² – у² = 8. Составить уравнение эллипса, проходящего через точку М(4;6) и имеющего фокусы, которые совпадают с фокусами данной гиперболы.

 

6. Найти точки пересечения параболы у² = 8х с эллипсом, у которого правый фокус совпадает с фокусом этой параболы, большая полуось равна 4 и фокусы лежат на оси Ох.

 

7. Фокусы гиперболы лежат в точках F₁(Ö7;0) и F₂(-Ö7;0). Гипербола проходит через точку А(2;0). Найти уравнения ее асимптот.

 

8. Найти параметр р параболы у² = 2рх, если известно, что эта парабола проходит через точки пересечения прямой у = х с окружностью х² + у² – 6х = 0.

 

9. Найти точки пересечения параболы у² = х с прямой, проходящей через фокус этой параболы параллельно ее директрисе.

10. Через правый фокус гиперболы 4х² – 5у² = 20 проведены прямые, параллельные ее асимптотам. Определить точки пересечения этих прямых с гиперболой.

 

11. Написать уравнение окружности, чтобы ее центр совпадал с фокусом параболы у² = 8х и чтобы окружность прошла через начало координат.

 

12. Оси гиперболы совпадают с осями координат. Гипербола проходит через точки пересечения параболы х² = 2у с прямой х – 2у + 6 = 0. Составить уравнение этой гиперболы.

 

13. Эллипс проходит через точку пересечения прямой 3х + 2у = 7 с параболой у² = 4х (взять точку с меньшей абсциссой). Оси эллипса совпадают с осями координат. Составить уравнение этого эллипса, если его эксцентриситет равен 0,6.

 

14. Эксцентриситет гиперболы в 2 раза больше углового коэффициента ее асимптоты. Гипербола проходит через точку М(3;-1), ее действительная ось лежит на оси Ох, а центр в начале координат. Найти точки пересечения этой гиперболы с окружностью х² + у² = 10.

 

15. Написать уравнение параболы, вершина которой находится в начале координат, а осью симметрии является ось Ох, если известно, что расстояние от ее фокуса до центра окружности х² + у² – 10х – 8у+ + 25 = 0 равно 5.

 

16. Составить каноническое уравнение эллипса, правая вершина которого совпадает с правым фокусом гиперболы 8х² – у² = 8. Эллипс проходит через точки пересечения параболы у² = 12х с данной гиперболой.

 

17. Вычислить расстояние от фокуса гиперболы 4х² – 5у² = 20 до ее асимптот. Найти эксцентриситет этой гиперболы.

 

 

18. Найти точки пересечения параболы у² = х с окружностью, которая проходит через начало координат, имеет центр на оси Ох и радиус, равный 5.

 

19. Составить уравнение эллипса, если его фокусы совпадают с фокусами гиперболы 4х² – 5у² = 20, а эксцентриситет эллипса равен 0,6.

 

20. Окружность имеет центр в левой вершине гиперболы х² – 4у² = =16 и радиус, равный вещественной полуоси этой гиперболы. Найти точки пересечения этой окружности с асимптотами данной гиперболы.

 

21. Составить уравнение гиперболы, имеющей эксцентриситет e= 1,5, если известно, что ее фокусы совпадают с фокусами эллипса 2х² + +5у² = 30.

 

22. Составить уравнение окружности, диаметром которой служит отрезок прямой х + у – 4 = 0, вырезанный параболой у² = 2х.

 

23. Найти расстояние от фокуса параболы 8у = х² до прямой 3х + +4у + 2 = 0.

 

24. Написать уравнение окружности, проходящей через точки А(3;0) и В(-1;2), если известно, что ее центр лежит на прямой х – у + 2 = 0.

 

25. Вычислить расстояние от центра окружности х² + у² = 10х до асимптот гиперболы х² – 4у² = 20.

 

26. Составить каноническое уравнение эллипса, сумма полуосей которого равна 8 и расстояние между фокусами равно 8.

 

27. В эллипс 24х² + 49у² = 1176 вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.

 

28. Составить уравнение окружности, проходящей через точки А(5;0) и В((1;4), если центр ее лежит на прямой х + у = 3.

29. Написать каноническое уравнение эллипса, у которого эксцентриситет равен 0,8, а большая полуось больше малой полуоси на 2 единицы.

 

30. Найти каноническое уравнение гиперболы, проходящей через точку М(Ö40;2) и имеющей асимптоты 3у = ±х.

 

 

ЗАДАЧА 6

Изобразить на чертеже области, определяемые системой неравенств.

Вариант 1

.

Вариант 2

.

Вариант 3

.

Вариант 4

.

Вариант 5

.

Вариант 6

.

Вариант 7

.

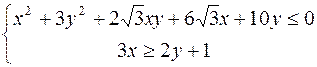Вариант 8

.

Вариант 9

.

Вариант 10

.

Вариант 11

.

Вариант 12

.

Вариант 13

.

Вариант 14

.

Вариант 15

.

Вариант 16

.

Вариант 17

.

Вариант 18

.

Вариант 19

.

Вариант 20

.

Вариант 21

.

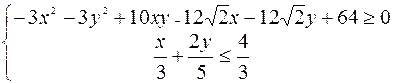Вариант 22

.

Вариант 23

.

Вариант 24

.

Вариант 25

.

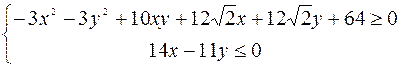Вариант 26

.

 

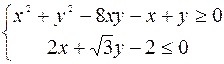Вариант 27

.

Вариант 28

.

Вариант 29

.

Вариант 30

.

 

ЗАДАНИЕ 7

Привести к каноническому виду уравнение поверхности второго порядка с помощью теории квадратичных форм. Сделать чертеж поверхности в канонической системе координат.

1. х²+4ху+у²+z²=0.

2. х²+4ху+у²+2z²-6=0.

3. х²+4ху+у²-2z²=0.

4. х²+4ху+у²-3z²+12=0.

5. 2х²-6ху+2у²+z²=0.

6. 2х²-6ху+2у²+2z²-25=0.

7. 3х²+4ху+3у²+2z²-50=0.

8. 3х²+4ху+3у²-2z²=0.

9. 3х²+4ху+3у²-z²-100=0.

10. 2хz-3y²=0.

11. х²+4ху+у²-4z²-12=0.

12. 2ху-3z²=0.

13. х²+4хz+5у²+z²=0.

14. 3x²-2yz=0.

15. х²+6хz+5у²+z²-15=0.

16. 2х²+4у²+2z²+2xz-12=0.

17. 2х²-3у²+2z²+2xz=0.

18. 2х²-3у²+2z²-2xz-12=0.

19. 2х²-3у²+2z²-6xz+36=0.

20. 2х²+2у²+2z²+2yz-1=0.

21. 2х²-2у²-2yz -2z²+1=0.

22. 2х²-2у²-6yz- 2z²-1=0.

23. х²-у²-yz-z²=0.

24. х²-3у²-2yz-3z²-1=0.

25. х²+3у²+2yz+3z²+1=0.

26. 3х²-3у²-2yz-3z²=0.

27. 2х²-3у²-2yz-3z²-1=0.

28. х²+2у²+6yz+2z²+10=0.

29. 3х²+2у²-6yz+2z²-10=0.

30. х²+у²-6yz+z²=0.

 

ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

ПО ТЕМЕ «ВЕКТОРНАЯ АЛГЕБРА»

1. Даны точки А (4;4;9), B (1;9;-1), C (3;7;4) и D (4;7;6).

Вычислить:

а) объем тетраэдра ABCD;

б) площадь грани ABC;

в) угол между вектором и высотой тетраэдра, опущенной из вершины А;

г) проекцию вектора на вектор ;

д) координаты вектора в базисе и .

 

2. Найти площадь и угол между диагоналями параллелограмма, построенного на векторах и , если 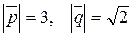и угол между векторами и равен 45^о.

 

ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

ПО ТЕМЕ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

1. Даны точки А (-2;-5), B (4;4) и C (8;-3). Пусть C ₁ – точка, симметричная точке C относительно прямой АВ. Написать уравнение прямой, проходящей через точку C ₁ и составляющей угол 30^о с осью Ох.

2. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А (-4;0) и В(4;0) равна 40.

 

3. Написать уравнение прямой, проходящей через правый фокус эллипса 9х² +25у²=225 и точку А(-1;-3).

 

4. Написать уравнение плоскости, проходящей через прямую 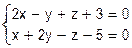параллельно прямой .

 

ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ

«АЛГЕБРА И ГЕОМЕТРИЯ»

 

1. Определители. Вычисление определителей порядка n ≤ 3. Свойства определителей.

2. Миноры. Алгебраические дополнения. Теорема Лапласа.

3. Матрицы. Основные операции над матрицами.

4. Обратная матрица. Алгоритм вычисления.

5. Ранг матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

6. Линейная зависимость и независимость строк (столбцов) матрицы. Теорема Кронекера–Капелли.

7. Системы линейных алгебраических уравнений. Формулы Крамера.

8. Системы линейных алгебраических уравнений. Решение с помощью обратной матрицы.

9. Системы линейных алгебраических уравнений. Метод Гаусса.

10. Векторы и простейшие действия над ними.

11. Базис в пространстве, на плоскости и на прямой. Компонента (составляющая) вектора по (вдоль) оси. Проекция вектора на ось. Направляющие косинусы вектора. Теоремы о векторах.

12. Системы координат: декартова, декартова прямоугольная, полярная, цилиндрическая, сферическая.

13. Скалярное произведение векторов. Угол между векторами. Условие коллинеарности векторов.

14. Ориентация тройки векторов. Векторное произведение векторов. Свойства векторного произведения. Выражение векторного произведения через координаты сомножителей.

15. Смешанное произведение векторов. Свойства смешанного произведения. Выражение смешанного произведения через координаты сомножителей.

16. n – мерный вектор и векторное пространство.

17. Линейные преобразования. Действия над линейными преобразованиями.

18. Собственные значения и собственные векторы линейного преобразования.

19. Евклидово пространство. Ортогональные преобразования.

20. Квадратичные формы. Приведение к каноническому виду.

21. Алгебраическая линия на плоскости. Понятие об инвариантах. Параметрические уравнения линий.

22. Прямая на плоскости: параметрические уравнения, каноническое уравнение, уравнение с угловым коэффициентом.

23. Прямая на плоскости: общее уравнение, уравнение в отрезках, векторное уравнение.

24. Прямая на плоскости: уравнение прямой, проходящей через две точки; уравнение прямой, проходящей через данную точку в данном направлении; угол между прямыми; условия параллельности и перпендикулярности прямых.

25. Окружность и эллипс.

26. Гипербола.

27. Парабола.

28. Общее уравнение линии второго порядка и его инварианты. Классификация линий второго порядка и определение параметров канонических уравнений.

29. Общее уравнение линии второго порядка. Определение положения канонической системы координат.

30. Плоскость: общее уравнение, параметрические уравнения, векторное уравнение, уравнение в отрезках.

31. Уравнение плоскости, проходящей через три точки. Расстояние от точки до плоскости. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.

32. Прямая в пространстве: параметрические уравнения, каноническое уравнение, общее уравнение.

33. Угол между двумя прямыми. Расстояние от точки до прямой. Кратчайшее расстояние между двумя прямыми.

34. Параметрические уравнения поверхностей. Конусы. Уравнения, не содержащие одной из координат.

35. Поверхности вращения. Алгебраическая поверхность.

36. Поверхности второго порядка. Эллипсоиды. Гиперболоиды.

37. Поверхности второго порядка. Эллиптический параболоид. Гиперболический параболоид.

38. Приведение к каноническому виду уравнения поверхности второго порядка с помощью теории квадратических форм.