РУКОВОДСТВО
К решению задач индивидуального задания
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
 |


 |
Р Г Г М У
Санкт-Петербург
Одобрено научно-методическим советом РГГМУ
УДК 51
Веретенников В. Н. Руководство к решению задач индивидуального задания «Обыкновенные дифференциальные уравнения». – СПб.: Изд. РГГМУ. 2008. – 38 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.
Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н
© Российский государственный гидрометеорологический университет (РГГМУ), 2007.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями.
Целью математического образования является:
· Воспитание достаточно высокой математической культуры.
· Привитие навыков современных видов математического мышления.
· Привитие навыков использования математических методов и основ математического моделирования в практической деятельности.
Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.
В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Обыкновенные дифференциальные уравнения"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
1.1. Основные понятия. Дифференциальные уравнения первого порядка
Дифференциальным уравнением называется соотношение, связывающее независимую переменную, неизвестную функцию и ее производные (или дифференциалы).
В случае, когда неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, дифференциальное уравнение называется обыкновенным.
Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящей в уравнение.
Обыкновенное дифференциальное уравнение порядка  в самом общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до порядка
в самом общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до порядка  включительно и имеет вид
включительно и имеет вид
 . (1.1)
. (1.1)
В этом уравнении 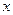 − независимая переменная,
− независимая переменная,  − неизвестная функция, а
− неизвестная функция, а 
 − производные неизвестной функции.
− производные неизвестной функции.
Обыкновенное дифференциальное уравнение первого порядка имеет вид
 , (1.2)
, (1.2)
а если его удастся решить относительно производной, то оно запишется в нормальной форме:
 . (1.3)
. (1.3)
В некоторых случаях уравнение (1.3) удобно записывать в виде

или в виде
 ,
,
которое является частным случаем более общего уравнения в дифференциальной форме
 , (1.4)
, (1.4)
где  − известные функции. Уравнение в симметричной форме (1.4) удобно тем, что переменные
− известные функции. Уравнение в симметричной форме (1.4) удобно тем, что переменные 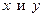 в нем равноправны, т. е. каждую из них можно рассматривать как функцию другой.
в нем равноправны, т. е. каждую из них можно рассматривать как функцию другой.
Решением дифференциального уравнения называется такая дифференцируемая функция  , которая при подстановке в уравнение вместо неизвестной функции обращает его в верное равенство.
, которая при подстановке в уравнение вместо неизвестной функции обращает его в верное равенство.
Справедлива
Теорема 1 (Коши). Если функция  непрерывна в точке
непрерывна в точке  и в ее окрестности, то существует решение
и в ее окрестности, то существует решение  уравнения (1.3), такое, что
уравнения (1.3), такое, что  . Если непрерывна также частная производная
. Если непрерывна также частная производная 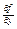 данной функции, то это решение единственно.
данной функции, то это решение единственно.
Общим решением уравнения первого порядка называется функция  , которая при любом значении произвольной постоянной
, которая при любом значении произвольной постоянной  является решением данного уравнения.
является решением данного уравнения.
Общее решение, полученное в неявном виде:  , называется общим интегралом дифференциального уравнения.
, называется общим интегралом дифференциального уравнения.
Построенный на плоскости  график всякого решения
график всякого решения  данного дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению
данного дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению  на плоскости
на плоскости  соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной
соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной  .
.
Часто среди всех решений дифференциального уравнения, определяемых его общим решением, требуется найти такое, которое удовлетворяет условиям:  , где
, где  и
и 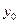 − заданные числа. Геометрически это значит, что требуется найти интегральную кривую, проходящую через заданную точку плоскости
− заданные числа. Геометрически это значит, что требуется найти интегральную кривую, проходящую через заданную точку плоскости  .
.
Задание таких условий  , называется заданием начальных условий и записывается коротко так:
, называется заданием начальных условий и записывается коротко так:

 .
.
Решения, которые получаются из общего решения  при определенном значении произвольной постоянной
при определенном значении произвольной постоянной  , называются частными.
, называются частными.
Задача нахождения частного решения, удовлетворяющего начальным условиям  , называется задачей Коши.
, называется задачей Коши.
Замечание. У дифференциального уравнения может существовать решение (интеграл), которое невозможно получить из общего решения ни при каких значениях произвольных постоянных  . Такие решения (интегралы) называются особыми.
. Такие решения (интегралы) называются особыми.
Например, проверкой можно убедиться, что уравнение 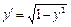 имеет общее решение
имеет общее решение  , в то же время функция
, в то же время функция  также является решением этого уравнения, но это решение не может быть получено из общего решения ни при каких значениях
также является решением этого уравнения, но это решение не может быть получено из общего решения ни при каких значениях  , т. е. является особым.
, т. е. является особым.
Графиком особого решения является интегральная кривая, которая в каждой своей точке имеет общую касательную с одной из интегральных кривых, определяемых общим решением. (Такая кривая называется огибающей семейства интегральных кривых.)
Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОСНОВНЫХ ПОНЯТИЙ
Исходя из геометрического смысла производной  , заметим, что уравнение первого порядка
, заметим, что уравнение первого порядка  задает в каждой точке
задает в каждой точке  плоскости
плоскости  значение
значение  тангенса угла наклона (к оси
тангенса угла наклона (к оси  ) касательной к графику решения, проходящего через эту точку. Величину
) касательной к графику решения, проходящего через эту точку. Величину  далее будем называть угловым коэффициентом. Если теперь в каждой точке
далее будем называть угловым коэффициентом. Если теперь в каждой точке  задать с помощью некоторого вектора направление касательной, определяемое значением
задать с помощью некоторого вектора направление касательной, определяемое значением  , то получится так называемое поле направлений. Таким образом, геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной.
, то получится так называемое поле направлений. Таким образом, геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной.
Общее решение – однопараметрическое семейство интегральных кривых  , где
, где  − параметр.
− параметр.
Частное решение уравнения  − интегральная кривая
− интегральная кривая  , угловые коэффициенты касательных к которой определяются данным дифференциальным уравнением.
, угловые коэффициенты касательных к которой определяются данным дифференциальным уравнением.
В области  , в которой выполняются все условия теоремы 1 (Коши), для уравнения (1.3) можно выделить однопараметрическое семейство линий
, в которой выполняются все условия теоремы 1 (Коши), для уравнения (1.3) можно выделить однопараметрическое семейство линий  , каждая из которых называется изоклиной. Как следует из определения, вдоль каждой изоклины поле направлений постоянно, т. е.
, каждая из которых называется изоклиной. Как следует из определения, вдоль каждой изоклины поле направлений постоянно, т. е.  .
.
Нахождение изоклин и направлений вдоль них позволяет упорядочить поле направлений и приближенно построить интегральные линии данного дифференциального уравнения, т. е. графически проинтегрировать это уравнение.
Пример 1.1. Для дифференциального уравнения  с начальным условием
с начальным условием  общее решение имеет вид
общее решение имеет вид  . Оно представляет собой семейство окружностей. Если теперь в общее решение подставить начальные данные, то получим
. Оно представляет собой семейство окружностей. Если теперь в общее решение подставить начальные данные, то получим  , т. е.
, т. е.  . Следовательно, частное решение, удовлетворяющее указанному начальному условию, есть
. Следовательно, частное решение, удовлетворяющее указанному начальному условию, есть  . Геометрически это означает, что из всего множества окружностей, представляющих общее решение, выбирается одна окружность, проходящая через точку
. Геометрически это означает, что из всего множества окружностей, представляющих общее решение, выбирается одна окружность, проходящая через точку  .
.
Полагая  , находим изоклины
, находим изоклины  данного уравнения. Они представляют собой проходящие через начало координат прямые линии, вдоль которых поле направлений определяется равенством
данного уравнения. Они представляют собой проходящие через начало координат прямые линии, вдоль которых поле направлений определяется равенством  . Придавая
. Придавая  различные значения, находим соответствующие изоклины, вдоль которых направление поля характеризуется углом
различные значения, находим соответствующие изоклины, вдоль которых направление поля характеризуется углом  наклона к оси
наклона к оси  касательной к интегральной линии. Необходимые вычисления приведены в виде таблицы.
касательной к интегральной линии. Необходимые вычисления приведены в виде таблицы.
Таблица 1.1

| 
| 
| 
| 
| |
 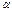
| 
| 
| 
| 
| |
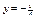
| 
| 
| 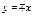
| 
| 
|

 ??
??
Что есть что?
1) Дифференциальное уравнение  .
.

 2) Общее решение
2) Общее решение 

3) Частное решение 

 y
y
 |



x

 !!
!!
1.2. Методы интегрирования дифференциальных уравнений первого порядка
Рассмотрим методы нахождения решений дифференциальных уравнений первого порядка, Отметим, что общего метода нахождения решений не существует. Обычно рассматривают типы уравнений, и для каждого из них находят свой способ нахождения решения.
1.2.1. Дифференциальные уравнения с разделяющимися переменными.
Уравнением с разделяющимися переменными (тип I) называются уравнения вида
 ,
,  ,
,  .
.
Чтобы решить уравнение типа I надо разделить переменные, привести уравнение к виду с разделенными переменными  и проинтегрировать почленно.
и проинтегрировать почленно.

 ??
??
Как разделять переменные?
Для отыскания решения уравнения  или
или  нужно разделить в нем переменные. Для этого
нужно разделить в нем переменные. Для этого
Ø заменим  ,
,
Ø умножим обе части уравнения  (
( должны быть только в числителях),
должны быть только в числителях),
Ø разделим обе части уравнения на такое выражение, чтобы в одну часть уравнения входило только 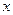 , в другую – только
, в другую – только  , т. е.
, т. е.  ,
,
Ø проинтегрируем обе части.
При делении обеих частей уравнения на выражение, содержащее неизвестные  , могут быть потеряны решения (особые), обращающие это выражение в нуль.
, могут быть потеряны решения (особые), обращающие это выражение в нуль.
Пусть дифференциальное уравнение задано в дифференциальной форме (1.4). В частном случае, когда каждая из функций  является произведением двух функций, одна из которых – функция только
является произведением двух функций, одна из которых – функция только 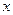 , а вторая – только
, а вторая – только  , т. е. когда
, т. е. когда
 ,
,
уравнение примет вид
 .
.
Разделение переменных производится делением обеих частей полученного уравнения на произведение 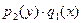 , в котором
, в котором 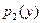 − функция только
− функция только  , являющаяся множителем
, являющаяся множителем  , а
, а  − функция только
− функция только 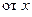 , являющаяся множителем
, являющаяся множителем  . После деления на это произведение уравнение примет вид
. После деления на это произведение уравнение примет вид
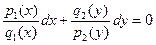 .
.
Это уравнение называется уравнением с разделенными переменными:  находится функция, зависящая только
находится функция, зависящая только 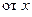 ,
,  − только
− только  .
.

 !!
!!
Пример 2.1.1. Решить уравнение с разделяющимися переменными  .
.
▲ 1. 
2.  ,
,
3.  . ▼
. ▼

 ??
??
Для успешного усвоения темы необходимо
Уметь: 1. интегрировать, поэтому таблицу основных интегралов надо знать на память;
2. потенцировать любое выражение → 
Помнить признаки дифференциальных уравнения с разделяющимися переменными и метод их решения.
Понимать смысл всех употребляемых терминов, понятий и символов.
Если Вы усвоили смысл термина «произвольная постоянная», то Вам должно быть понятно, что:  и то, что произвольную постоянную можно писать в любой части равенства.
и то, что произвольную постоянную можно писать в любой части равенства.
!!
 |  |
Пример. 2.1.2. Найти частное решение уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
.
▲ 1.  ,
,
2.  ,
,  .
.
3.  .
.
 ,
,

 . Обратите внимание, как записана произвольная постоянная.
. Обратите внимание, как записана произвольная постоянная.
После потенцирования получаем общий интеграл: 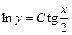 .
.
При отыскании частного решения к указанному выше алгоритму добавляется еще одна новая операция:
Найти  , подставив в общее решение (интеграл) начальные условия, и записать частное решение.
, подставив в общее решение (интеграл) начальные условия, и записать частное решение.
4.  . Частный интеграл:
. Частный интеграл: 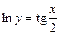 .
.
1.2.2. Однородные дифференциальные уравнении (тип  )
)
Функция 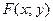 называется однородной функцией измерения
называется однородной функцией измерения  относительно аргументов
относительно аргументов  , если равенство
, если равенство
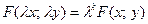
справедливо для любого  , при котором функция
, при котором функция 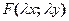 определена,
определена, 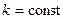 .
.
Дифференциальное уравнение в нормальной форме 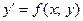 называется однородным относительно переменных
называется однородным относительно переменных 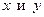 , если
, если  − однородная функция нулевого измерения относительно своих аргументов, т. е.
− однородная функция нулевого измерения относительно своих аргументов, т. е.  .
.
Однородное дифференциальное уравнение в нормальной форме всегда можно записать в виде (положив  )
)  .
.
Уравнение в дифференциальной форме  называется однородным, если функции
называется однородным, если функции  − однородные функции одного измерения.
− однородные функции одного измерения.
Однородное уравнение с помощью замены  сводится к уравнению с разделяющимися переменными относительно
сводится к уравнению с разделяющимися переменными относительно 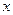 и новой функции
и новой функции  .
.

 ??
??
Чтобы решить однородное уравнение, нужно:
Ø Ввести подстановку  сводится к уравнению типа
сводится к уравнению типа  .
.
Ø Разделить переменные и проинтегрировать уравнение типа  .
.
Ø Результат интегрирования упростить, пропотенцировать, если нужно, и записать общий интеграл, вернувшись к исходной переменной.

 !!
!!
Пример 2.2.1. Решить уравнение  .
.
▲ Здесь  . Имеем:
. Имеем:  .
.
Следовательно, 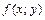 − однородная функция нулевого измерения, потому уравнение является однородным.
− однородная функция нулевого измерения, потому уравнение является однородным.
1.  − уравнение типа
− уравнение типа  .
.
2.  ;
;
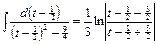 ;
;  .
.
В однородных уравнениях лучше  относить
относить  .
.
3. Общий интеграл 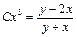 . ▼
. ▼
Пример 2.2.2. Найти решение уравнения 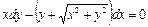 .
.
▲ Коэффициенты  соответственно равны:
соответственно равны:  .
.
Функции  являются однородными функциями первого измерения. Действительно,
являются однородными функциями первого измерения. Действительно,
 ,
,
 .
.
Поэтому исходное уравнение является однородным. Приведем уравнение к нормальному виду, разделив его  . Имеем
. Имеем  .
.
1.  − уравнение типа
− уравнение типа  .
.
2.  .
.
 .
.
3. Общий интеграл  . ▼
. ▼
Пример 2.2.3. Найти частное решение уравнения  , если
, если  .
.
▲ Преобразуем уравнение к нормальному виду:  .
.
Здесь  . Имеем:
. Имеем:
Следовательно, 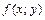 − однородная функция нулевого измерения, потому уравнение является однородным.
− однородная функция нулевого измерения, потому уравнение является однородным.
1.  − уравнение типа
− уравнение типа  .
.
2.  .
.
3.  . Общий интеграл
. Общий интеграл  .
.
4. Найдем  .
. 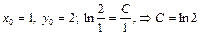 . Частный интеграл
. Частный интеграл  . ▼
. ▼
1.2.3. Линейные дифференциальные уравнения
Дифференциальное уравнение называется линейным, если функция и ее производная входят в него в первой степени (линейно):  − тип
− тип  .
.
Для решения уравнения типа  применяется метод подстановки
применяется метод подстановки
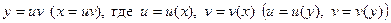 − непрерывные функции,
− непрерывные функции,
а также метод вариации произвольной постоянной.

 ??
??
Что необходимо для решения линейных уравнений:
Уметь
Ø интегрировать по частям  .
.
Ø заменять переменную  ,
,
стрелки в скобках указывают на два способа замены переменной.
Знать, что для определения двух неизвестных величин нужна система из двух уравнений.
!!


Если в уравнении

ввести замену 
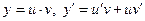 ,
,
где  . Для определения
. Для определения  можно составить две идентичные системы
можно составить две идентичные системы




из верхнего уравнения получается одна система уравнений,  а из нижнего уравнения − вторая
а из нижнего уравнения − вторая 
В каждой из систем первое уравнение выбрано произвольно потому, что две неизвестные  нельзя найти из одного уравнения. Пользоваться можно любой системой.
нельзя найти из одного уравнения. Пользоваться можно любой системой.
Пример 2.3.1. Решить уравнение  .
.
▲ Прежде всего, нужно проверить признаки линейного уравнения:  входят в уравнение в первой степени (линейно). Затем следует выполнить следующие операции:
входят в уравнение в первой степени (линейно). Затем следует выполнить следующие операции:
1. Положить  , тогда
, тогда  . Подставить
. Подставить  в исходное уравнение:
в исходное уравнение:
 .
.
2. Составить систему для определения 
Решить первое уравнение системы. 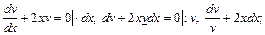
 . При определении
. При определении 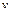 не нужно писать произвольную постоянную, ибо
не нужно писать произвольную постоянную, ибо  достаточно знать с точностью до постоянной.
достаточно знать с точностью до постоянной.
3. Подставить во второе уравнение системы  и решить полученное:
и решить полученное:
 .
.
4. Записать ответ:  − общее решение. ▼
− общее решение. ▼
Пример 2.3.2. Найти частное решение уравнения  , если
, если 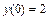 .
.
▲ Линейное уравнение ( входят в уравнение в первой степени).
входят в уравнение в первой степени).
1. 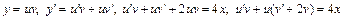
2.  .
.
3. 
 .
.
4.  − общее решение.
− общее решение.
5. Чтобы найти частное решение, нужно начальное условие подставить в общее решение и определить  :
:
 .
.
Частное решение:  . ▼
. ▼
Пример 2.3.3. Решить уравнение  .
.
▲ Так как переменная  в квадрате, это уравнение не будет линейным относительно функции
в квадрате, это уравнение не будет линейным относительно функции  , но будет линейным, если считать переменную
, но будет линейным, если считать переменную  функцией, а
функцией, а  аргументом. Имеем
аргументом. Имеем  ,
,
 .
.
1.  .
.
2.  .
.
3.  .
.
4. Общее решение:  . ▼
. ▼
Метод вариации произвольной постоянной для решения линейных уравнений
Пример 2.3.4. Решить линейное уравнение  методом вариации.
методом вариации.
▲ 1. Решить сначала уравнение без правой части (однородное линейное уравнение)  :
:
 .
.
2. Положить  и, подставив
и, подставив  в исходное уравнение, решить его:
в исходное уравнение, решить его:
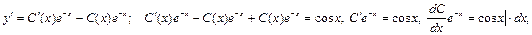

 ;
;
 .
.
 .
.
3. Подставить  в выражение
в выражение  и записать общее решение
и записать общее решение
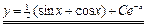 .
.  ▼
▼
Если этот метод решения Вам понравился,
то Вы его можете использовать наряду с методом замены переменной.
1.2.4. Уравнение Бернулли
Одним из уравнений, сводящихся к линейным уравнениям, является уравнение Бернулли (тип IV), которое имеет вид
 , где
, где  .
.
Преобразование уравнения Бернулли в линейное уравнение будем проводить в такой последовательности:
1) умножим обе части уравнения  ;
;
2) введем подстановку 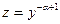 . Обе части этого равенства продифференцируем:
. Обе части этого равенства продифференцируем:
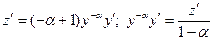 ;
;
3) полученное линейное уравнение  можно решить методом замены переменной или методом вариации.
можно решить методом замены переменной или методом вариации.
4) возвратимся к искомой функции, заменяя 
 .
.
Пример 2.4.1. Решить уравнение Бернулли  .
.
▲ Сведем это уравнение к линейному уравнению.
1) Для этого обе части поделим  (умножим
(умножим  ):
):  ,
,
2) Положим  , тогда
, тогда  − линейное уравнение. 3) Решим его методом замены переменной:
− линейное уравнение. 3) Решим его методом замены переменной:
1.  .
.
2. Запишем систему  .
.
3. Подставим 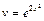 во второе уравнение системы:
во второе уравнение системы:  ,
,

 .
.
4.  . Общий интеграл
. Общий интеграл 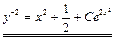 . ▼
. ▼
1.2.5. Уравнения в полных дифференциалах и сводящиеся к ним
Уравнение

называется уравнением в полных дифференциалах (тип V), если его левая часть есть полный дифференциал некоторой функции:
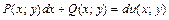 .
.
В этом случае уравнение можно записать в виде
 ,
,
откуда следует, что соотношение  является его общим интегралом. Выражение
является его общим интегралом. Выражение  , где
, где  − непрерывные функции вместе со своими частными производными
− непрерывные функции вместе со своими частными производными 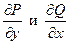 в некоторой области
в некоторой области  , есть полный дифференциал тогда и только тогда, когда
, есть полный дифференциал тогда и только тогда, когда  во всей области
во всей области  .
.
Что нужно знать для успешного обучения решению уравнений типа V и сводящихся к ним
1. Понимать смысл символов  .
.
2. Уметь интегрировать частные дифференциалы:
Пусть  , тогда
, тогда  ;
;
если 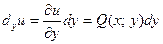 , то
, то  .
.
Пример 2.5.1. Решить уравнение  .
.
▲ Прежде чем решать уравнение, проверим его признаки.
Здесь  . Находим:
. Находим:  , значит,
, значит,  , и данное уравнение есть уравнение в полных дифференциалах (тип V).
, и данное уравнение есть уравнение в полных дифференциалах (тип V).
 ;
;
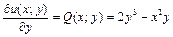 .
.
1. Интегрируя первое уравнение  и считая
и считая  постоянным, находим
постоянным, находим
 .
.
Здесь произвольная постоянная зависит от переменной  , так как искомая функция
, так как искомая функция  есть функция двух переменных, а интегрирование выполнялось по переменной
есть функция двух переменных, а интегрирование выполнялось по переменной  .
.
2. Дифференцируя функцию  , получим
, получим  . Но
. Но
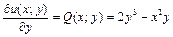
поэтому  , откуда
, откуда  .
.
Таким образом,
 .
.
С другой стороны
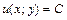 ,
,
поэтому,  − общий интеграл данного уравнения.) ▼
− общий интеграл данного уравнения.) ▼
Как определять тип дифференциального уравнения первого порядка
Ø Прежде всего, нужно знать типы всех уравнений и признаки каждого из них на память.
Ø Затем усвоить алгоритм распознавания типа дифференциального уравнения, который состоит из проверки признаков типов дифференциальных уравнений.
Ниже приводится сводная таблица типов дифференциальных уравнений первого порядка и их признаков.
| Тип | Название диф. ур-я | Общий вид | Признаки | Метод решения |
| I | Уравнение с разделяющимися переменными |  или
или
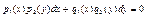
| В правой части (функции 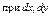 ) стоит произведение двух функций, каждая из которых зависит только от одной переменной ) стоит произведение двух функций, каждая из которых зависит только от одной переменной
| Разделение переменных и интегрирование |
| II | Однородное уравнение | 

| 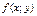 − однородная функция нулевого измерения; − однородная функция нулевого измерения;
 − однородные функции одного измерения − однородные функции одного измерения
| 
|
| III | 1. Линейное уравнение относительно  2. Линейное уравнение относительно
2. Линейное уравнение относительно 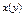
| 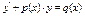

| Функция и ее производная входят в уравнение в первой степени (линейно) | 

|
| IV | 1. Уравнение Бернулли относительно  2. Уравнение Бернулли относительно
2. Уравнение Бернулли относительно 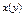
| 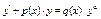

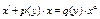

| Отличается от соответствующего линейного уравнения правой частью | Делим 


|
| V | Уравнение в полных дифференциалах | 
| 
|
Как только данное уравнение совпадает по признакам (или общему виду) с одним из типов, его следует решать, воспользовавшись соответствующим этому типу методом.
Чтобы определить дифференциального уравнения, его лучше записать либо в виде
 ,
,
либо:
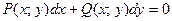 −
−
как проще.
Решение задач 1-5 типового варианта
Найти общее решение (общий интеграл) дифференциального уравнения.
1.  .
.
▲ Здесь  можно записать как (разложив на множители оба выражения):
можно записать как (разложив на множители оба выражения):  , где каждый из сомножителей зависит только от одной переменной. Следовательно, данное уравнение является уравнением с разделяющимися переменными (тип I).
, где каждый из сомножителей зависит только от одной переменной. Следовательно, данное уравнение является уравнением с разделяющимися переменными (тип I).
Ø 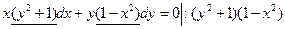 .
.
Ø 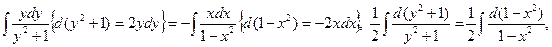
 .
.
Следовательно, общим интегралом исходного уравнения является
 . ▼
. ▼
2.  .
.
▲ Здесь функции  представляют собой выражения, в которых каждый из сомножителей зависит только от одной переменной. Поэтому исходное уравнение является уравнением типа I.
представляют собой выражения, в которых каждый из сомножителей зависит только от одной переменной. Поэтому исходное уравнение является уравнением типа I.
Ø  .
.
Ø  ,
,
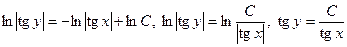
 − общий интеграл дифференциального уравнения. ▼
− общий интеграл дифференциального уравнения. ▼
3.  .
.
▲ Запишем уравнение в нормальной форме
 .
.
 . Следовательно,
. Следовательно,  − однородная функция нулевого измерения, потому исходное уравнение однородное.
− однородная функция нулевого измерения, потому исходное уравнение однородное.
Ø  ,
,
Ø  .
.
 ,
,
 .
.
Ø Общий интеграл исходного уравнения:  . ▼
. ▼
4. Найти частное решение дифференциального уравнения
 .
.
▲ Приведем подобные члены относительно  и преобразуем уравнение, выделив производную
и преобразуем уравнение, выделив производную  ,
,
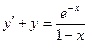 .
.
Функция и ее производная входят в уравнение в первой степени (линейно). Следовательно, данное уравнение линейное. Решаем его.
Ø 
Ø  ;
;
Ø 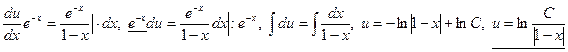 ;
;
Ø Тогда  − общее решение исходного уравнения.
− общее решение исходного уравнения.
Ø Находим  , используя начальное условие:
, используя начальное условие:  .
.
 .
.
Окончательно получаем, что частное решение исходного уравнения имеет вид
 . ▼
. ▼
5. Найти общее решение дифференциального уравнения
 .
.
▲ Преобразуем уравнение для того, чтобы определить его тип. Получим
 .
.
Отличается от соответствующего линейного уравнения правой частью  . Следовательно, данное уравнение является уравнением Бернулли.
. Следовательно, данное уравнение является уравнением Бернулли.
1.  .
.
2.  − линейное уравнение относительно
− линейное уравнение относительно 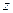 .
.
3. Решим его методом замены переменной.
Ø  .
.
Ø 
 ;
;
 ,
,
Ø 

 .
.
Имеем
 ,
,
 .
.
 .
.
Следовательно,
 .
.
Ø






