Факультет Прикладной математики
Кафедра "Математическое обеспечение систем обработки информации и управления" (группа МС-61).
Задания составил доцент кафедры
МОСОИиУ Марков В.Н.
Москва 2009
Задания на курсовую работу
Задание № 1
На СМО смешанного типа, состоящую из  каналов обслуживания и
каналов обслуживания и  мест в накопителе очереди, поступает простейший поток заявок с интенсивностью
мест в накопителе очереди, поступает простейший поток заявок с интенсивностью  .Поток обслуживания каждым каналом также простейший с интенсивностью
.Поток обслуживания каждым каналом также простейший с интенсивностью  . Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
1. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса. Оценить предельные (финитные) значения вероятностей состояний и вероятностей того, что а) длина очереди не превышает 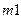 мест и б) число занятых каналов обслуживания составляет не более
мест и б) число занятых каналов обслуживания составляет не более  .
.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1. Оценить по результатам моделирования вероятность того, что очередь превысит
, превышающем не менее чем на порядок время переходного процесса п.1. Оценить по результатам моделирования вероятность того, что очередь превысит 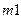 мест за принятое время работы СМО, если система функционирует без отказов.
мест за принятое время работы СМО, если система функционирует без отказов.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами  и
и  . Способ продвижения модельного времени – с постоянным шагом. Шаг
. Способ продвижения модельного времени – с постоянным шагом. Шаг 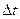 принимается на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок в каналах обслуживания.
принимается на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок в каналах обслуживания.
4, Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с
результатами моделирования имитационного (п.п. 2,3 и 4).
Таблица исходных данных
| a | b | 
| 
| 
| 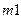
| 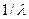
| 
| |
Задание № 2
На СМО смешанного типа, состоящую из  каналов обслуживания и
каналов обслуживания и  мест в накопителе очереди, поступает простейший поток заявок с интенсивностью
мест в накопителе очереди, поступает простейший поток заявок с интенсивностью  .
.
Каждый канал имеет свою интенсивность простейшего потока обслуживания  ,
,  =1,…,
=1,…,  . Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
1. Используя прием расширения пространства состояний свести процесс в системе к марковскому. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей приведенных состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса.
Оценить предельные (финитные) значения вероятностей состояний и вероятностей того, что а) длина очереди не превышает 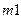 мест и б) вероятности занятия для каждого из каналов обслуживания.
мест и б) вероятности занятия для каждого из каналов обслуживания.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс, Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1.
, превышающем не менее чем на порядок время переходного процесса п.1.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что потоки обслуживания каждым каналом равномерные с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что потоки обслуживания каждым каналом равномерные с параметрами 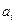 и
и 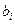 ,
,  =1,…,
=1,…,  . Способ продвижения модельного времени – с постоянным шагом. Шаг
. Способ продвижения модельного времени – с постоянным шагом. Шаг 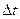 принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3 и 4).
Таблица исходных данных
| a1 | b1 | a2 | b2 | 
| 
| 
| 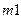
| 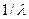
| 
| 
| 
| |
| ---- | ||||||||||||
| ---- | ||||||||||||
| ---- |
Задание № 3
Рассматривается так называемая замкнутая СМО, состоящая из  одинаковых устройств, каждое из которых в любой момент может выйти из строя и потребовать обслуживания для устранения неисправности. Интенсивность простейшего потока неисправностей каждого устройства равна
одинаковых устройств, каждое из которых в любой момент может выйти из строя и потребовать обслуживания для устранения неисправности. Интенсивность простейшего потока неисправностей каждого устройства равна  . Количество каналов обслуживания, устраняющих неисправности равно
. Количество каналов обслуживания, устраняющих неисправности равно  . Каждый канал обслуживает одно устройство. Поток обслуживания каждым каналом простейший с интенсивностью
. Каждый канал обслуживает одно устройство. Поток обслуживания каждым каналом простейший с интенсивностью  . Если в момент выхода устройства из строя все каналы заняты, устройство становится в очередь на обслуживание и ждет, пока какой либо из каналов не освободится. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров.
. Если в момент выхода устройства из строя все каналы заняты, устройство становится в очередь на обслуживание и ждет, пока какой либо из каналов не освободится. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров.
1. Определить переменные состояния. Составить граф переходов и систему дифференциальных уравнений относительно вероятностей состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса. Оценить (финитные) значения вероятностей состояний и вероятности того, что а) число неисправных устройств в очереди не превышает 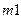 и б) число занятых каналов обслуживания составляет не более
и б) число занятых каналов обслуживания составляет не более  .
.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1.
, превышающем не менее чем на порядок время переходного процесса п.1.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами 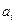 и
и 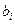 ,
,  =1,…,n. Способ продвижения модельного времени – с постоянным шагом. Шаг
=1,…,n. Способ продвижения модельного времени – с постоянным шагом. Шаг 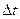 принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3и 4).
Таблица исходных данных
| a1 | b1 | a2 | b2 | 
| 
| 
| 
| 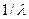
| 
| 
| |
| – | – | – | |||||||||
Задание № 4
Рассматривается так называемая замкнутая СМО, состоящая из  одинаковых устройств, каждое из которых в любой момент может выйти из строя и потребовать обслуживания для устранения неисправности. Интенсивность простейшего потока неисправностей каждого устройства равна
одинаковых устройств, каждое из которых в любой момент может выйти из строя и потребовать обслуживания для устранения неисправности. Интенсивность простейшего потока неисправностей каждого устройства равна  . Количество каналов обслуживания, устраняющих неисправности равно
. Количество каналов обслуживания, устраняющих неисправности равно  . Каждый канал реализует простейший поток обслуживания с интенсивностью
. Каждый канал реализует простейший поток обслуживания с интенсивностью  ,
,  = 1,...,
= 1,...,  Если в момент выхода устройства из строя все каналы заняты, устройство становится в очередь на обслуживание и ждет, пока какой либо из каналов не освободится. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов по возрастанию их номеров.
Если в момент выхода устройства из строя все каналы заняты, устройство становится в очередь на обслуживание и ждет, пока какой либо из каналов не освободится. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов по возрастанию их номеров.
1. Используя прием расширения пространства состояний свести процесс в системе к марковскому. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей приведенных состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса.
Оценить предельные (финитные) значения вероятностей состояний и вероятностей того, что а) длина очереди не превышает 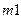 мест и б) число занятых каналов обслуживания составляет не менее
мест и б) число занятых каналов обслуживания составляет не менее  .
.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1.
, превышающем не менее чем на порядок время переходного процесса п.1.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами 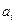 и
и 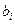 ,
,  =1,…,
=1,…,  . Способ продвижения модельного времени – с постоянным шагом. Шаг
. Способ продвижения модельного времени – с постоянным шагом. Шаг 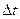 принимается на 2-3 порядка меньше среднего интервала между поступлением заявок или среднего времени обработки заявок каналами
принимается на 2-3 порядка меньше среднего интервала между поступлением заявок или среднего времени обработки заявок каналами
обслуживания.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3 и 4).
Таблица исходных данных
| a1 | b1 | a2 | b2 | 
| 
| 
| 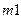
| 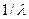
| 
| 
| |
Задание №5
Рассматривается СМО смешанного типа с ограниченным временем ожидания, состоящая из  каналов обслуживания и
каналов обслуживания и  мест в накопителе очереди. Входной поток заявок простейший с интенсивностью
мест в накопителе очереди. Входной поток заявок простейший с интенсивностью  . Поток обслуживания каждым каналом простейший с интенсивностью
. Поток обслуживания каждым каналом простейший с интенсивностью  , поток отказов в связи с превышением времени ожидания на одну заявку, стоящую в очереди, простейший с интенсивностью
, поток отказов в связи с превышением времени ожидания на одну заявку, стоящую в очереди, простейший с интенсивностью 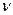 . Порядок занятия свободных каналов по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
. Порядок занятия свободных каналов по возрастанию их номеров. При отсутствии свободных мест в очереди пришедшая заявка получает отказ.
1. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса. Оценить предельные (финитные) значения вероятностей того, что длина очереди не превышает 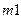 мест, а число занятых каналов обслуживания составляет не более
мест, а число занятых каналов обслуживания составляет не более  .
.
2 Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1.
, превышающем не менее чем на порядок время переходного процесса п.1.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами  и
и  . Способ продвижения модельного времени – с постоянным шагом. Шаг
. Способ продвижения модельного времени – с постоянным шагом. Шаг 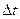 принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или временами обработки заявок каналами
принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или временами обработки заявок каналами
обслуживания.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3..
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3..
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3 и 4).
Таблица исходных данных
| a | b | 
| 
| 
| 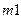
| 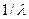
| 
| 
| |
Задание № 6
Рассматривается обслуживающая система, процесс функционирования которой представляет собой циклический ветвящийся процесс. Система представляет собой произвольный объект обслуживания, который может находиться в следующих состояниях:
·  – исправен, работает;
– исправен, работает;
·  – неисправен, остановлен; ведется поиск неисправности;
– неисправен, остановлен; ведется поиск неисправности;
·  – неисправность незначительна, проводится мелкий ремонт;
– неисправность незначительна, проводится мелкий ремонт;
·  – неисправность средней тяжести, проводится средний ремонт;
– неисправность средней тяжести, проводится средний ремонт;
·  – неисправность серьезная, проводится капитальный ремонт;
– неисправность серьезная, проводится капитальный ремонт;
·  – ремонт окончен, проводится подготовка к пуску.
– ремонт окончен, проводится подготовка к пуску.
Процесс, протекающий в системе – марковский, т.е. поток отказов и потоки обслуживания на всех этапах ремонта являются простейшими с интенсивностями 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. 
1. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса. Оценить предельные (финитные) значения вероятностей того, что объект нормально функционирует, или находится в ремонте по той или иной категории.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени, превышающем примерно на порядок время переходного процесса п.1.
3. Провести моделирование при условии, что поток обслуживания в местах проведения ремонта равномерный с параметрами 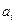 и
и 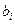 ,
,  =1,2,3 соответственно мелкому, среднему и капитальному ремонтам. Способ продвижения модельного времени – с постоянным шагом. Шаг принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или моментами освобождения каналов.
=1,2,3 соответственно мелкому, среднему и капитальному ремонтам. Способ продвижения модельного времени – с постоянным шагом. Шаг принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или моментами освобождения каналов.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2, 3 и 4)..
Таблица исходных данных

| 
| 
| 
| 
| 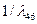
| 
| 
| 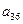
| 
| 
| 
| 
| 
| |
| 1.5 | ||||||||||||||
| 0.5 | 1.5 | |||||||||||||
| 1.5 |
Задание №7
На многофазную СМО смешанного типа, состоящую из n1, n2, n3 каналов обслуживания и m1, m2, m3 мест в накопителях очередей 1–ой, 2–ой и 3–ей фаз соответственно. Входной поток простейший с интенсивностью  . Потоки обслуживания каналами простейшие с интенсивностями
. Потоки обслуживания каналами простейшие с интенсивностями 
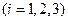 . Дисциплины очередей первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При невозможности помещения заявки в следующую фазу обработки канал блокируется. При отсутствии свободных мест в очереди первой фазы пришедшая заявка получает отказ.
. Дисциплины очередей первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. При невозможности помещения заявки в следующую фазу обработки канал блокируется. При отсутствии свободных мест в очереди первой фазы пришедшая заявка получает отказ.
1. Определить состояния, составить граф переходов и систему дифференциальных уравнений относительно вероятностей состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса. Оценить финитные значения вероятностей состояний и вероятностей того, что а) заблокированным окажется хотя бы один канал и б) общее число занятых работой каналов составляет не более.  .
.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс. Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем примерно на порядок время переходного процесса п.1. Оценить по результатам моделирования вероятности состояний, средние времена занятости каналов и пребывания заявки в системе.
, превышающем примерно на порядок время переходного процесса п.1. Оценить по результатам моделирования вероятности состояний, средние времена занятости каналов и пребывания заявки в системе.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что поток обслуживания равномерный с параметрами 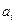 и
и 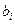
 =1,2,3.
=1,2,3.
Способ продвижения модельного времени – с постоянным шагом. Шаг 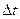 принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или моментами освобождения каналов
принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или моментами освобождения каналов
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
. 5. Сравнить результаты аналитического моделирования (п. 1)
с результатами моделирования имитационного (п.п. 2,3 и 4).
Таблица исходных данных

| 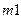
| 
| 
| 
| 
| 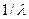
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
| – | – | – | – | – | ||||||||||||
| – | – | – | – | – | – | – | ||||||||||
| – | – | – | ||||||||||||||
| – | – | – | – | – |
Задание №8
На СМО смешанного типа, состоящую из  каналов обслуживания и
каналов обслуживания и  мест в накопителе очереди, поступает простейший поток заявок с интенсивностью
мест в накопителе очереди, поступает простейший поток заявок с интенсивностью  .
.
Каждый канал имеет свою интенсивность простейшего потока обслуживания  ,
,  =1,…,
=1,…,  . Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. Время от времени каналы отказывают и сразу начинают ремонтироваться. Потоки неисправностей и восстановления простейшие (параметры r и r1). Заявка с неоконченной обработкой остается в канале и дообслуживается после ремонта.
. Дисциплина очереди первым пришел – первым обслуживаешься. Порядок занятия свободных каналов – по возрастанию их номеров. Время от времени каналы отказывают и сразу начинают ремонтироваться. Потоки неисправностей и восстановления простейшие (параметры r и r1). Заявка с неоконченной обработкой остается в канале и дообслуживается после ремонта.
Перед каждой обработкой канал проходит наладку. Поток наладки простейший с параметром r2.
1. Используя прием расширения пространства состояний свести процесс в системе к марковскому. Составить граф переходов состояний и систему дифференциальных уравнений относительно вероятностей приведенных состояний. Используя средства программной системы MATLAB решить эти уравнения и оценить время переходного процесса.
Оценить предельные (финитные) значения вероятностей состояний и вероятностей того, что а) длина очереди не превышает 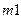 мест и б) вероятности занятия для каждого из каналов обслуживания.
мест и б) вероятности занятия для каждого из каналов обслуживания.
2. Средствами визуального моделирования Simulink-Stateflow программной системы MATLAB составить имитационную модель СМО, рассматривая процесс в системе как марковский процесс, Способ продвижения модельного времени – по особым состояниям. Провести моделирование на интервале времени  , превышающем не менее чем на порядок время переходного процесса п.1.
, превышающем не менее чем на порядок время переходного процесса п.1.
3. Аналогично п.2 составить имитационную модель процесса в СМО, основываясь на представлении системы в понятиях  – схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что потоки обслуживания каждым каналом равномерные с параметрами
– схемы. Провести моделирование при заданных параметрах потоков, а также при условии, что потоки обслуживания каждым каналом равномерные с параметрами 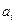 и
и 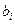 ,
,  =1,…,
=1,…,  . Способ продвижения модельного времени – с постоянным шагом. Шаг
. Способ продвижения модельного времени – с постоянным шагом. Шаг 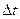 принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
принимается примерно на 2-3 порядка меньше среднего интервала между поступлением заявок или средними временами обработки заявок каналами обслуживания.
4. Составить программу в виде m-файла имитационной модели СМО, основываясь на представлении системы в понятиях  – схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
– схемы. Способ продвижения модельного времени – по особым состояниям. Провести моделирование в соответствии с заданием п.1,2 и 3.
5. Сравнить результаты аналитического моделирования (п. 1) с результатами имитационного (п.п. 2,3 и 4).
Таблица исходных данных
| a1 | b1 | a2 | b2 | 
| 
| 
| 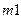
| 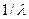
| r | r1 | 
| r2 | 
| |
Таблица заданий на курсовую работу
| Бондарев А.. | ||||
| Бучнев Г. | ||||
| Гольцов Ф. | ||||
| Дымбицкая В.* | ||||
| Евсеев И. | ||||
| Капралов Е. | ||||
| Ковалевский А. | ||||
| Коняхин И. | ||||
| Красноперова Е. | ||||
| Мизраки Д. | ||||
| Постовский Л. | ||||
| Пронина А. | ||||
| Старичихин М. | ||||
| Стронский Н. | ||||
| Чистяков В. | ||||
| . | ||||
| . | ||||






