В качестве входных воздействий, на которые ищется реакция системы, приняты воздействия, описываемые элементарными математическими функциями, то есть такими, на которые можно разложить любые произвольные функции. В теории управления в качестве элементарных функций используются:
1) единичная ступенчатая функция 1(t);
2) единичная импульсная функция δ(t);
3) весовая функция (t)
Единичная ступенчатая функция определяется выражением:
Единичная импульсная функция, которая также называется δ – функцией или функцией Дирака, определяется как производная от единичной ступенчатой функции. Поскольку в момент времени t = 0 функция 1(t) претерпевает разрыв, то ее производная не существует (обращается в бесконечность). Таким образом, единичная импульсная функция равна:
(t) = 
Для физической интерпретации δ - функции целесообразно ее рассматривать как предел, к которому стремится прямоугольный импульс единичной площади длительностью ∆t и амплитудой 1/∆t. Графически этот процесс представлен на рисунке 4.
Рис. 4 – Физическая интерпретация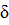 
– функции при 
и 1/∆t 
Интеграл δ - функции:
Зная весовую функцию g(t), можно найти реакцию динамического звена на любое входное воздействие. Если, например, представить непрерывный входной сигнал произвольной формы совокупностью δ-функций:
x(t) = 
Tо сигнал на выходе линейного звена определяется как:
y(t)= 
Рис. 5 – а) Типовые входные взаимодействия в виде единичной ступенчатой функции 1(t) единичной импульсной 
(в), функций и соответствующие им отклики системы виде переходной характеристики h(t) (б) и весовой функции g(t) (г).
Весовая функция (t) – реакция системы на единичный импульс при нулевых начальных условиях.
где τ - вспомогательное время интегрирования. По весовой функции можно также определить передаточную функцию динамического звена:
W(p) = 
Аналогично, зная переходную характеристику, можно определить реакцию системы на произвольное входное воздействие, учитывая, что переходная характеристика и импульсная переходная функция однозначно связаны между собой соотношениями:
[5,6]
Гармонические колебания.
Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Уравнение гармонического колебания имеет вид
Или
где х — отклонение колеблющейся величины в текущий момент времени t от среднего за период значения (например, в кинематике — смещение, отклонение колеблющейся точки от положения равновесия); А — амплитуда колебания, т.е. максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность A совпадает с размерностью x; ω (радиан/с, градус/с) — циклическая частота, показывающая, на сколько радиан (градусов) изменяется фаза колебания за 1 с; (ωt + φ) (радиан, градус) — полная фаза колебания (сокращённо — фаза, не путать с начальной фазой); φ (радиан, градус) — начальная фаза колебаний, которая определяет значение полной фазы колебания (и самой величины x) в момент времени t = 0. [7]
Заключение
Изучена система САУ, ее виды, устройство и основные характеристики. Такие как частотные характеристики. Рассмотрены и изучены такие частотные характеристики как: амплитудно – фазовая характеристика (АФХ), амплитудно – частотная характеристика (АЧХ), фазочастотную характеристику(ФЧХ), вещественно частотную характеристику (ВЧХ), мнимую частотную характеристику (МЧХ). Рассмотрены временные характеристики САУ. Изучены: единичная ступенчатая функция, единичная импульсная функция. Изучены гармонические колебания, рассмотрены их основные законы и характеристики. Сделаны выводы по все аспектам работы.