Введение
Цель овладения аппаратом построения временных и частотных характеристик систем управления состоит в создании теоретической базы для освоения математического аппарата исследования линейных систем автоматического управления (САУ), основных элементов и характеристик САУ, а также методов анализа САУ на устойчивость и качество управления, способов корректировки свойств линейных САУ.
Система САУ
Система автоматического управления (САУ) – комплекс устройств, обеспечивающих автоматическое изменение ряда координат (или одной координаты) объекта управления с целью установления желаемого режима работы объекта (рисунок 1). Под желаемым следует понимать такой режим, при котором достигается цель управления: обеспечивается достижение заданных значений регулируемых величин или оптимизируется определенный критерий качества управления.
САУ могут быть системами управления разомкнутыми (без обратной связи), системами управления замкнутыми (с обратной связью) или комбинированными системами автоматического управления. Широкое распространение получили САУ для стабилизации определенных координат объекта управления, программного и следящего управления. При значительных изменениях параметров объекта управления, переменных во времени характеристиках внешних возмущений и помех. Некоторые сложные задачи оптимизации управления объекта управления могут быть решены с помощью систем экстремального регулирования. Задачи согласованного управления многомерных объектов с несколькими противоречивыми критериями качества решаются с помощью теории сложных систем управления. Примером таких систем служат иерархические системы управления.
В зависимости от свойств элементов системы различают линейные и нелинейные САУ, системы с постоянными или переменными параметрами и с переменной структурой. Виды и способы преобразования сигналов в САУ позволяют выделять непрерывные, импульсные, цифровые (дискретные) и т.п.

Рис. 1 – Схема разновидностей систем САУ.
Частотные характеристики САУ
Наряду с методом временных характеристик в теории автоматического управления широко используются методы частотных характеристик, которые определяют поведение системы при подаче на ее вход гармонических колебаний.
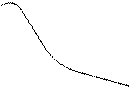
Амплитуда, фаза, действительная и мнимая части частотной функции могут быть графически представлены в виде амплитудно - фазовой, действительной, мнимой, амплитудной и фазовой частотных характеристик. Геометрическое место концов векторов частотной функции при различных частотах определяет амплитудно-фазовую частотную характеристику (АФЧХ).
Зависимость амплитуды от частоты называется амплитудно - частотной характеристикой (АЧХ): Ар(ω)= 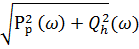 где Р(ω) = A(ω)cosφ(ω) — вещественная частотная характеристика; Q(ω) = A(ω)sinφ(ω) — мнимая частотная характеристика. Зависимость фазы от частоты называется фазо-частотной характеристикой: φ(ω) = arctg [Q (ω)/Р (ω)]. Каждая из этих частотных характеристик определяет свойства функциональных звеньев и САУ в целом. Примерный (наиболее общий) вид частотных характеристик автоматической системы показан на рисунке 2. [1,2]
где Р(ω) = A(ω)cosφ(ω) — вещественная частотная характеристика; Q(ω) = A(ω)sinφ(ω) — мнимая частотная характеристика. Зависимость фазы от частоты называется фазо-частотной характеристикой: φ(ω) = arctg [Q (ω)/Р (ω)]. Каждая из этих частотных характеристик определяет свойства функциональных звеньев и САУ в целом. Примерный (наиболее общий) вид частотных характеристик автоматической системы показан на рисунке 2. [1,2]
 а) Q(ω)
а) Q(ω)





 F (ω)
F (ω)

 φ
φ
|

 б) W (ω)
б) W (ω)
|

 ω
ω
в) д)
 P (ω)
P (ω)
 |

 ω
ω
 г) Q (ω)
г) Q (ω)

 ω
ω

 φ(ω)
φ(ω)
 |

 ω
ω
 |
Рис. 2 – Графики частотных характеристик.
Построение частотных характеристик звеньев, и в особенности системы в целом, значительно упрощается, если прологарифмировать выражение для частотной функции, представленной в показательной форме: lg W (jω) = lg A (ω) + jφ (ω)/2,3. Полученное выражение определяет логарифмическую амплитудно-фазовую частотную характеристику, у которой вещественная часть равна логарифму модуля частотной функции, а мнимая часть — аргументу частотной функции. Эта характеристика может быть представлена двумя самостоятельными характеристиками — логарифмической амплитудной и фазовой частотными характеристиками. Логарифмическая амплитудная характеристика (ЛАЧХ). Эта характеристика определяет изменение логарифма модуля частотной функции при изменении частоты. На графике обычно используют логарифмическую сетку; логарифм модуля откладывают по оси ординат, а логарифм частоты — по оси абсцисс, как показано на рисунке 3.



















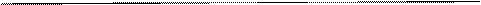 20
20
 15
15
 10
10
 5
5
 0
0
 -5 ω
-5 ω
0,1 0,2 0,3 0,4 0,6 1,0 2 3 4 5 6 8 10




 Декада Декада
Декада Декада



 Октава Октава
Октава Октава
0,1 0,2 0,4



 lg ω
lg ω
0 1 2
Рис. 3 – Логарифмическая сетка ЛАЧХ.
Так как G(ω) определяет логарифм отношения амплитуды на выходе к амплитуде на входе и характеризует степень усиления системой входного сигнала, то эту величину измеряют в единицах, принятых для усилительных устройств. Однако логарифмическая единица бел считается слишком крупной, поэтому величина G(ω) выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Децибел равен одной десятой части бела. Если бы A(ω) было отношением мощностей, то перед логарифмом амплитуды должен был стоять множитель 10. Так как A(ω) представляет собой отношение не мощностей, а перемещений, скоростей, напряжений, токов и т. п., то увеличение этого отношения в десять раз будет соответствовать увеличению мощностей в сто раз, что соответствует двум белам или двадцати децибелам. Это и определяет величину множителя 20. Один децибел соответствует изменению амплитуды в 10-20 раз. Для оценки диапазона частот при построении логарифмических характеристик используют единицы, применяемые в акустике — октаву и декаду. Если величины двух частот ωn и ωi отличаются друг от друга в два раза, то говорят, что они отличаются на одну октаву: ωn/ωi = 2, или log2 (ωn/ωi) = log22 = 1 окт. Если величины двух частот отличаются друг от друга в 10 раз то говорят, что они отличаются на декаду: ωn/ωi = 10, или lg (ωn/ωi) = lg10= 1 дек. Для определения частоты в декадах следует найти десятичный логарифм от данной частоты. Иногда используется координатная логарифмическая сетка, по оси абсцисс которой откладывается в логарифмическом масштабе частота, а по оси ординат — логарифм модуля частотной функции, т. е. логарифм отношения амплитуд выхода и входа. Логарифмическая фазовая характеристика (ЛФЧХ). Эта характеристика определяет изменение фазы в градусах при изменении частоты. Величина фазы в градусах откладывается по оси ординат соответственно выражению, а по оси абсцисс откладывается частота в логарифмическом масштабе. Для ряда реальных автоматических систем существует однозначная зависимость между ЛАХ и ЛФХ. Такие системы называются минимально-фазовыми, поскольку ЛФЧХ, соответствующая заданной ЛАЧХ, имеет наименьшее значение фазы. Дадим определения всем указанным характеристикам.
Амплитудно–фазовой характеристикой (АФХ) называется зависимость отношения выходной величины системы к входной величине, выраженного в комплексной форме, от частоты в установившемся режиме (см. рис. 1, а).
Амплитудно–частотной характеристикой (АЧХ) называется зависимость от частоты отношения амплитуды синусоидальной величины на выходе звена к амплитуде синусоидальной величины на входе (см. рис. 1, б).
Фазочастотной характеристикой (ФЧХ) называется зависимость разности фаз синусоидальных колебаний на выходе и входе системы(см. рис. 1, д).
Вещественной частотной характеристикой (ВЧХ) называется зависимость величины проекции АФХ на вещественной оси Р (w) от частоты входного синусоидального воздействия(см. рис. 1, в).
Мнимой частотной характеристикой (МЧХ) называется зависимость величины проекции АФХ на мнимой оси Q (w) от частоты входного синусоидального воздействия(см. рис. 1, г).
Частотные характеристики лежат в основе частотных методов исследования САУ, которые получили широкое распространение благодаря их наглядности и сравнительной простоте. Они позволяют не только исследовать свойства системы в установившемся режиме, но и судить об устойчивости системы, оценить качество процесса управления. [3,4]






