При рассмотрении стационарной модели процесса предполагается, что параметры процесса не зависят от времени. В этом случае левая часть уравнений (6) – (10) приравнивается нулю.
Для расчета статики процесса используется процедура Stat B06 [6]. В качестве независимых переменных выбираются 
и R. Определению подлежат величины D и 
.
1. Концентрация НК в дистилляте cвязана с расходом дистиллята уравнением общего МБ (3):
, (14)
где задается из области ограничений, накладываемых на состав кубового остатка.
2. Выбирается значение D и по формуле (14) определяется 
. Величина D в каждом цикле расчета вычисляется как среднее арифметическое значений, ограничивающих D слева и справа
. (15)
Для первого цикла:
, 
,
где 
– минимальный отбор при заданной чистоте кубового , что соответствует максимальной физически реализуемой чистоте дистиллята, равной единице; 
– максимальное физически реализуемое значение отбора дистиллята, равное расходу питания.
3. Используя D (15), по уравнению общего баланса (2), (5) рассчитываются величины W и 
.
4. С помощью уравнений (6) – (11), в которых левая часть равна нулю, определяется значения 
, при этом 
. Так, из выражения (6):
.
Равновесная концентрация НК в паровой фазе находится по уравнению (12)
.
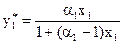Из (11) определяется концентрация 
:
.
Далее с помощью уравнения (7) определяется 
:
.
Продолжая расчет для каждой тарелки, определяются концентрация 
, 
, 
; 
, 
, 
; …; 
, 
, :
.
5. Проверяется правильность выбора D. Если D выбрано верно, то должно равняться , рассчитанной по формуле (14). Геометрически это соответствует точке О на рис. 2.
|
Рис. 2. Геометрическая интерпретация процедуры Stat B06
Если 
, то значение D необходимо изменять до тех пор, пока не выполнится условие 
.
Направление изменения D следующее: если 
, то в качестве правой границы 
берется значение 
из предыдущего цикла расчета, а левая граница остается прежней 
, далее повторяется расчет при новом среднем 
. Если же 
, то из предыдущего цикла расчета берется в качестве левой границы 
, а правая остается прежней.
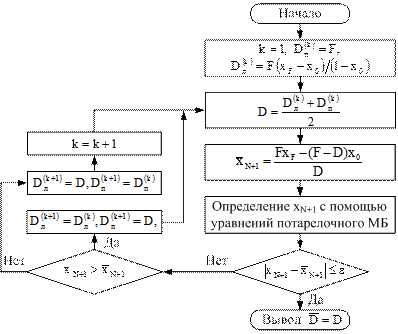
Блок-схема алгоритма процедуры приведена на рис. 3.
|
Рис. 3. Блок-схема алгоритма процедуры Stat B06
В результате расчета статики процесса определяется значение D, при котором выполняются условия общего и потарелочного баланса при заданном флегмовом числе R.
Задание на лабораторную работу
В колонну подается смесь пентана (С5Н12) и гексана (С6Н14).
В начальный момент времени 
на входе аппарата наблюдаются возмущающие воздействия: отклонения расхода и состава сырья. Значения возмущений: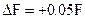 
, 
. Управляющей функцией является расход флегмы 
, заданный в области допустимых значений
,
, 
,
где 
– первое приближение управления на первом такте, соответствующее статическому режиму работы колонны L. Коэффициент а принимается равным одному из следующих значений:
.
Требования к показателям переходного процесса записываются в виде ограничений на значения концентрации НК (целевого компонента смеси – пентана) на выходе колонны
, 
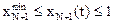; (27)
, 
. (28)
В качестве экономического показателя переходного процесса принимается технологическая себестоимость получаемого продукта, связанная с расходом тепла на нагрев куба колонны, концентрацией продуктов , , значениями возмущений F и 
:
. (29)
, (30)
где 
– стоимость единицы сырья; 
– стоимость тепла, подводимого с греющим паром в кипятильник; 
– максимально-допустимое значение себестоимости. Значение рассчитывается по уравнению (30) для заданных величин F, , , соответствующих статическому режиму.
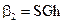
здесь S – стоимость 1 ккал тепла; G – расход греющего пара; h – теплосодержание пара.
Расход греющего пара G в кипятильник связан с расходом парового потока в колонне уравнением
,
где 
– молярная масса испаряемой смеси; V – мольный расход парового потока в колонне; 
, 
– теплота испарения смеси и конденсации греющего пара, соответственно.
Требуется определить управление, обеспечивающее выполнение ограничений (27) – (29), в дискретных точках 
.
Исходные данные
Расчет статики процесса (процедура Stat B06) проводится при
.
Обеспечение требования (27) в статическом режиме выполняется подбором величин 
и 
(табл. 1).
На рис. 4 приведена блок-схема алгоритма управления переходными режима моделируемой установки.
Рис. 4. Блок-схема алгоритма управления переходным режимом
Длительность тактов управления принята равной 
ч, управление 
в каждом такте постоянно; длительность переходного процесса – 
ч. Возмущение подается один раз – в начальный момент времени.
Решение системы дифференциальных уравнений строится численным методом Эйлера (см. приложение).
кг/кмоль, 
кг/кмоль;
кмоль; 
д.е./кмоль, 
д.е./ккал;
ккал/кг, 
ккал/кг, 
ккал/кг.
Численные значения конструктивных и режимных параметров, необходимых для проведения расчетов, представлены в таблице 1.
Таблица 1.
| № | F, кмоль/ч | xF, мол. доли | N | f | hmin | hmax | Rmin | Rmax | a |
| 0.60 | 0.40 | 0.65 | 1.30 |
Листинг программы
uses crt;
const N=50;
Nf=25;
kpd=0.65;
alpha=1.3;
x0z=0.23;
xn1z=0.974;
H=8;
R=16;
eps=0.01;
type matrix=array [0..(N+1)] of real;
var f1:text;
x,y,yzv,xs,ys,xd,yd:matrix;
F,D,W,L,V,xf,xn1,left,right,Mcp,b2,Gz,Cz,G,C,T,Jmax,Jmin,J11,J12,J21,J22,J3,Lstat,Lmin,Lmax,dL,x0sr,xn1sr,Csr:real;
i,j:byte;
procedure STATB06(F,D,W,L,V:real; var x,y:matrix);
begin
x[1]:=(V+W)*x[0]/(L+F);
yzv[1]:=alpha*x[1]/(1+x[1]*(alpha-1));
y[1]:=y[0]+kpd*(yzv[1]-y[0]);
for i:=1 to (Nf-1) do
begin
x[i+1]:=x[i]-V*(y[i-1]-y[i])/(L+F);
yzv[i+1]:=alpha*x[i+1]/(1+x[i+1]*(alpha-1));
y[i+1]:=y[i]+kpd*(yzv[i+1]-y[i]);
end;
x[Nf+1]:=((L+F)*x[Nf]-V*(y[Nf-1]-y[Nf])-F*xf)/L;
yzv[Nf+1]:=alpha*x[Nf+1]/(1+x[Nf+1]*(alpha-1));
y[Nf+1]:=y[Nf]+kpd*(yzv[Nf+1]-y[Nf]);
for i:=(Nf+1) to N do
begin
x[i+1]:=x[i]-V*(y[i-1]-y[i])/L;
yzv[i+1]:=alpha*x[i+1]/(1+x[i+1]*(alpha-1));
y[i+1]:=y[i]+kpd*(yzv[i+1]-y[i]);
end;
x[N+1]:=V*y[N]/(L+D);
y[N+1]:=x[N+1];
end;
begin
clrscr;
assign(f1,'Mb_po_tarelkam.txt');
rewrite(f1);
F:=390;
xf:=0.6;
left:=F*(xf-x0z)/(1-x0z);
right:=F;
repeat
D:=(right+left)/2;
xn1:=(F*xf-(F-D)*x0z)/D;
L:=D*R;
W:=F-D;
V:=D+L;
x[0]:=x0z/2;
y[0]:=x[0];
STATB06(F,D,W,L,V,x,y);
Lstat:=L;
if x[N+1]>xn1 then right:=D
else left:=D;
until abs(x[N+1]-xn1)<=eps;
for i:=0 to (N+1) do
begin
xs[i]:=x[i];
ys[i]:=y[i];
writeln(f1,'x[',i,']=',xs[i]:2:5,' y[',i,']=',y[i]:2:5);
end;
writeln('OTBET:');
writeln('L=',L:3:3,' ','xn1=',xn1:3:3,' ','D=',D:5:1);
writeln('F*xf=',(F*xf):5:3,' D*xd+W*xw=',(x[0]*W+x[N+1]*D):5:3);
close (f1);
end.
Результаты.
Рис. 4 – Результат работы программы.
x[0]=0.11500 y[0]=0.11500
x[1]=0.11500 y[1]=0.13418
x[2]=0.13314 y[2]=0.15515
x[3]=0.15296 y[3]=0.17788 (в таблицу)
x[4]=0.17445 y[4]=0.20234
x[5]=0.19757 y[5]=0.22842
x[6]=0.22224 y[6]=0.25600
x[7]=0.24831 y[7]=0.28488
x[8]=0.27561 y[8]=0.31481
x[9]=0.30391 y[9]=0.34553
x[10]=0.33296 y[10]=0.37674
x[11]=0.36246 y[11]=0.40810
x[12]=0.39211 y[12]=0.43930
x[13]=0.42161 y[13]=0.47001
x[14]=0.45065 y[14]=0.49995
x[15]=0.47896 y[15]=0.52885 x[42]=0.91904 y[42]=0.93364
x[16]=0.50628 y[16]=0.55650 x[43]=0.92477 y[43]=0.93849
x[17]=0.53242 y[17]=0.58270 x[44]=0.92992 y[44]=0.94286
x[18]=0.55719 y[18]=0.60734 x[45]=0.93456 y[45]=0.94678
x[19]=0.58049 y[19]=0.63033 x[46]=0.93872 y[46]=0.95029
x[20]=0.60223 y[20]=0.65163 x[47]=0.94246 y[47]=0.95345
x[21]=0.62236 y[21]=0.67122 x[48]=0.94581 y[48]=0.95627
x[22]=0.64089 y[22]=0.68915 x[49]=0.94881 y[49]=0.95879
x[23]=0.65783 y[23]=0.70545 x[50]=0.95149 y[50]=0.96105
x[24]=0.67324 y[24]=0.72020
x[25]=0.68720 y[25]=0.73350
x[26]=0.71212 y[26]=0.75254
x[27]=0.73235 y[27]=0.77075
x[28]=0.75170 y[28]=0.78807
x[29]=0.77009 y[29]=0.80443
x[30]=0.78748 y[30]=0.81981
x[31]=0.80382 y[31]=0.83419
x[32]=0.81910 y[32]=0.84758
x[33]=0.83332 y[33]=0.85998
x[34]=0.84650 y[34]=0.87142
x[35]=0.85866 y[35]=0.88195
x[36]=0.86984 y[36]=0.89159
x[37]=0.88008 y[37]=0.90039
x[38]=0.88944 y[38]=0.90841
x[39]=0.89795 y[39]=0.91569
x[40]=0.90569 y[40]=0.92229
x[41]=0.91270 y[41]=0.92826
