Ректификация – процесс разделения жидких и паро-жидкостных смесей путем многократного частичного испарения жидкости и конденсации паров. Процесс предполагает контакт потоков пара и жидкости, имеющих различную температуру, и обычно проводится в колонных аппаратах (рис. 1).
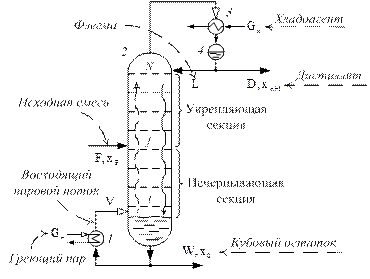
Рис. 1. Принципиальная технологическая схема ректификационной установки: 1 – кипятильник, 2 – ректификационная колонна, 3 – дефлегматор, 4 – флегмовая емкость.
При каждом контакте фаз из жидкости испаряется преимущественно легколетучий, или низкокипящий, компонент (НК), которым обогащаются пары, а из паров конденсируется преимущественно труднолетучий, или высококипящий, компонент (ВК), переходящий в жидкость. Такой двусторонний обмен компонентами, повторяемый многократно, позволяет получить в конечном счете пары, представляющие собой почти чистый НК. Эти пары после конденсации в отдельном аппарате образуют дистиллят (ректификат) и флегму – жидкость, возвращаемую для орошения колонны и взаимодействия с поднимающимися парами. Пары получают путем частичного испарения в кипятильнике остатка из куба колонны, являющего почти чистым ВК [3, 4].
Для описания нестационарных режимов работы ректификационных колонн широко применяются модели процесса с сосредоточенными [5, 6] и распределенными [1, 7] параметрами, основу которых составляют уравнения материального, теплового балансов, равновесия и кинетики массопередачи.
В данной работе математическая модель процесса ректификации представлена уравнениями материального баланса (МБ). При построении математической модели примем следующие допущения:
– исходная смесь и флегма подаются в колонну в виде жидкости при температуре кипения;
– расход пара по высоте колонны постоянный, т.е.  ,
,  ;
;
– расход жидкости по высоте укрепляющей секции колонны постоянный, т.е.  ,
, 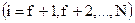 ;
;
– расход жидкости по высоте исчерпывающей секции колонны постоянный, т.е.  ,
, 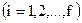 ;
;
– в паровой фазе в зоне массообмена принимается полное вытеснение, а в жидкой фазе – полное перемешивание.
Уравнения МБ процесса ректификации многокомпонентной смеси можно разделить на две группы:
ü общие уравнения баланса, составленные относительно входных и выходных потоков аппаратов установки (колонна, дефлегматор и др.);
ü уравнения потарелочного МБ, составленные для контактных ступеней разделения колонны.
Общие уравнения баланса:
 , (2)
, (2)
 , (3)
, (3)
 , (4)
, (4)
 , (5)
, (5)
где 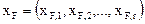 ,
,  ,
,  – r-мерные векторы концентраций компонентов в исходной смеси, дистилляте и кубовом остатке; F, L, V, D, W – величины питания, орошения (флегмы), парового потока в колонне, дистиллята и кубового продукта соответственно; R – флегмовое число.
– r-мерные векторы концентраций компонентов в исходной смеси, дистилляте и кубовом остатке; F, L, V, D, W – величины питания, орошения (флегмы), парового потока в колонне, дистиллята и кубового продукта соответственно; R – флегмовое число.
С учетом принятых допущений уравнения потарелочного МБ для исчерпывающей части колонны, расположенной, ниже тарелки питания  :
:
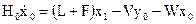 (куб колонны); (6)
(куб колонны); (6)
 ,
,  . (7)
. (7)
Для тарелки питания
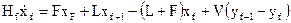 ; (8)
; (8)
Для укрепляющей части:
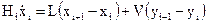 ,
,  ; (9)
; (9)
 (дефлегматор). (10)
(дефлегматор). (10)
 ,
,  , (11)
, (11)
где  – вектор концентраций компонентов в жидкой фазе на i-ой ступени разделения;
– вектор концентраций компонентов в жидкой фазе на i-ой ступени разделения;  – вектор концентраций компонентов в паровой фазе, уходящей с i-ой ступени разделения;
– вектор концентраций компонентов в паровой фазе, уходящей с i-ой ступени разделения;  – удерживающая способность по жидкости i-ой ступени разделения;
– удерживающая способность по жидкости i-ой ступени разделения;  – вектор концентраций компонентов в паре, равновесном с жидкостью состава
– вектор концентраций компонентов в паре, равновесном с жидкостью состава 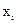 ;
;  – эффективность i-ой ступени разделения;
– эффективность i-ой ступени разделения;  ,
,  – давление и температура на i-ой ступени разделения.
– давление и температура на i-ой ступени разделения.
В случае ректификации бинарной смеси (состоящей из двух компонентов  ):
):
 , (12)
, (12)
здесь α – относительная летучесть компонентов смеси, равная отношению давлений паров чистых компонентов при одинаковом внешнем давлении.
Начальные условия для решения системы дифференциальных уравнений (6) – (10) имеют вид:
 ,
, 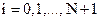 (13)
(13)
и определяются из расчета стационарной модели процесса.






