Цель работы: ознакомление с методикой многолучевой интерферометрии - метода полос (линий) равного хроматического порядка - для измерения толщины тонких слоев.
Тонкие пленки металлов, полупроводников и диэлектриков находят многочисленные практические применения. Они используются в качестве хорошо отражающих зеркальных покрытий, защитных слоев, преобразователей солнечной энергии, пассивных и активных элементов для пленочной электроники, интерференционных фильтров, поляризаторов и др. Одним из важнейших параметров тонких пленок является их толщина: геометрическая d или оптическая (произведение геометрической толщины на показатель преломления n вещества пленки). Известно множество способов измерения толщины пленок [14, 16, 17], среди которых наиболее точными являются оптические методы, основанные на интерференции света. Наибольшая точность обеспечивается применением методов многолучевой интерферометрии.
Интерференцию света можно наблюдать при падении света на прозрачную пластинку. На поверхностях пластинки происходит многократное отражение света, вследствие чего с каждой стороны пластины выходит ряд лучей с убывающими интенсивностями. Введем амплитудные коэффициенты отражения r и пропускания t как отношение амплитуды колебаний светового вектора соответственно отраженного ER или прошедшего ET света к амплитуде колебаний светового вектора E o падающего света. Энергетические коэффициенты отражения R и пропускания T равны
R = IR / Io = r2, (6.1)
T = IT / Io = t2, (6.2)
где IR и IT соответственно интенсивности отраженного от одной границы раздела и прошедшего через нее света, I o- интенсивность падающего света. Если коэффициент отражения поверхностей пластины мал (например, для стекла R = 0,04), то при рассмотрении интерференции обычно пренебрегают вкладом в результирующую интерференционную картину лучей, которые претерпели два и больше отражений (случай двухлучевой интеференции). Если же коэффициент отражения порядка единицы, следует учитывать вклад всех лучей. На практике увеличение R обычно достигается путем нанесения на поверхности высокоотражающих покрытий, в качестве которых чаще всего используются слои серебра. Интерференция в таком случае называется многолучевой.
Основные закономерности многолучевой интерференции рассмотрим для случая многократного отражения света при прохождении сквозь плоскопараллельную прозрачную пластину толщиной d и показателем преломления n, покрытую с двух сторон высокоотражающими слоями (рис. 6.1а). Отражение света от двух параллельных плоскостей приводит к образованию локализованных в бесконечности интерференционных полос равного наклона. Для расчета суммарной амплитуды проходящего света необходимо учитывать изменение амплитуды и разность фаз между двумя соседними лучами. При переходе через границу двух сред и при отражении света изменяется амплитуда колебаний светового вектора. Если пренебречь поглощением света, то
R + T = 1. (6.3)
 |
При каждом прохождении через границу пластина - среда и при каждом отражении на той же границе амплитуда волны уменьшается и соответственно амплитуды лучей 1¢, 2¢, 3¢, 4¢,... будут равны Ео t2, Ео t2r2, Ео t2r4, Е оt2r6,..., а лучей 1, 2, 3, 4,..., соответственно, - Е оr, Е оt2r, Е оt2r3, Е оt2r5,...; амплитуды образуют убывающие геометрические прогрессии. Если угол падения i мал, а длина пластины по сравнению с ее толщиной большая, количество лучей 1¢, 2¢, 3¢,... и 1, 2, 3,... будет очень большим (бесконечным). Тогда суммарная интенсивность прошедшего через пластинку и отраженного от пластинки света определяется соответственно соотношениями Эйри [13]
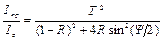, (6.4)
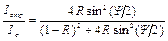. (6.5)
Разность фаз Y между двумя соседними лучами определяется формулой
Y = (2p/ l)2 nd cos r, (6.6)
где l - длина световой волны в вакууме, r - угол преломления (рис. 6.1).
Когерентные проходящие лучи света усиливаются (наблюдаются максимумы интенсивности), если выполняется условие
2 dn cos r = ml, (m = 0, 1, 2,...), (6.7)
и ослабляются (наблюдаются минимумы интенсивности), если
2 dn cos r = (2 m +1) l /2. (6.8)
Из соотношения (6.4) следует, что суммарная интенсивность в прошедшем свете будет иметь экстремальные значения, когда sin(Y /2) = 0 и
sin(Y /2) = ± 1:
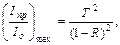
(6.9)
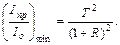(6.10)
Из соотношений (6.9) и (6.10) видно, что контрастность интерференционной картины зависит только от коэффициента отражения:
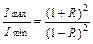. (6.11)
Как следует из формул Эйри, распределение интенсивности в многолучевой интерференционной картине сильно зависит от коэффициента отражения R. На рис. 6.2 приведены кривые распределения интенсивности прошедшего света в зависимости от Y для разных значений R. При R <<1 они имеют вид, типичный для двух интерферирующих пучков, максимумы и минимумы имеют одинаковую ширину. С увеличением R максимумы сужаются, а в промежутках между ними интенсивность становится очень малой. Для характеристики формы контура интерференционной полосы используется величина F, которая называется резкостью. Она определяется отношением разности фаз между двумя соседними максимумами к полуширине интерференционного экстремума e (рис. 6.2):
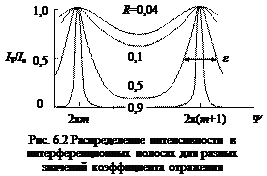F = 2p/e. (6.12)
Таким образом, характерной особенностью многолучевой интерференционной картины в проходящем свете при значениях R близких к единице является чередование контрастных узких максимумов и широких минимумов. В отраженном свете наблюдается дополнительная картина в виде узких темных полос на почти равномерном светлом фоне. Благодаря такому распределению интенсивности многолучевая интерференция получила важное практическое применение, в частности, при измерении толщины тонких (d < l) пленок. Повышение точности измерения связано с тем, что многолучевые интерференционные полосы по сравнению с двухлучевыми имеют значительно более высокую резкость F. Например, для R = 0,9 резкость полос достигает 30, а e уменьшается более, чем на порядок по сравнению с двухлучевой интерференцией. Благодаря этому обеспечивается возможность измерения координат полос с более высокой точностью. При толщинах слоев в диапазоне
3 - 2000 нм толщина может быть измерена с погрешностью менее 1 нм.
Еще более высокую точность измерений обеспечивают многолучевые интерференционные полосы равного хроматического порядка (РХП) [18]. Для их наблюдения используется интерферометр Фабри - Перо, состоящий из двух пластин, высокоотражающие поверхности которых установлены строго параллельно друг другу и разделены воздушным промежутком толщиной t (рис. 6.1б). На интерферометр падает под углом i» 0о коллимированный (параллельный) пучок белого света. В воздушном зазоре между пластинами возникает многолучевая интерференция. Отраженный или прошедший белый свет разлагается в спектр с помощью спектрального прибора, в фокальной плоскости которого наблюдается картина интерференции. Условие образования интерференционных экстремумов определяется общей формулой
2 t - (d/p)l = m l, (6.13)
где d = (b 1+ b 2)/2, а b 1 и b 2 - изменения фазы, возникающие при отражении света от каждого отражающего покрытия, m - порядок интерференции. Среди непрерывного спектра белого света обязательно найдутся такие длины волн l 1, l 2, l 3,..., соответственно, m, m +1, m +2,... порядков, для которых выполняется условие (6.13). В результате на месте непрерывного спектра получается набор светлых (в проходящем свете) или темных (в отраженном свете) интерференционных полос РХП. Их положение на шкале длин волн определяется исключительно оптической толщиной воздушного зазора интерферометра
t / l = (m +d /p)/2 (6.14)
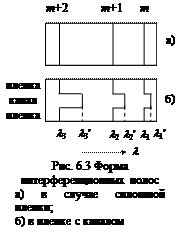
Согласно уравнению (6.14) полосы будут возникать для определенных значений t / l (рис. 6.3а).
Допустим, что толщина зазора t непрерывно меняется. Если пренебречь дисперсией фазы d (зависимостью d от l), то правая часть уравнения (6.14) для линии определенного порядка является постоянной величиной. Следовательно, изменение t должно приводить к такому изменению l экстремума, что для данного m t / l = const. Линии одного интерференционного порядка в проходящем свете окрашиваются в различные цвета. Отсюда происходит название линий - линии равного хроматического порядка.
Для получения резких контрастных линий РХП необходимо соблюдение сравнительно жестких условий, а именно: покрытия должны иметь высокую отражательную способность (R» 0,8 – 0,9), а падающий белый свет должен быть строго коллимированным. При высоком качестве поверхности исследуемого слоя и поверхности второй пластинки интерферометра, а также при тщательной установке этих поверхностей параллельно друг другу, погрешность измерения толщины слоя может быть доведена до 0,1 нм [16].
методика измерений.
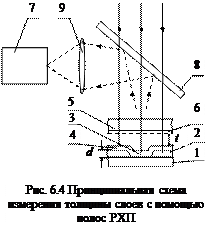Линии РХП можно использовать для измерения толщины тонких пленок, осажденных на стеклянную подложку. На оптически плоскую стеклянную пластинку 1 (рис. 6.4) наносится тонкая пленка 2, толщину которой необходимо измерить. В центре пластинки должна быть полоска, не покрытая пленкой (канал или канавка 3). Канал образует ступеньку, высота которой равна толщине пленки. Ступенька (канавка) в слое выполняется царапаньем, травлением или применением маски в процессе напыления. Затем на пленку с каналом в высоком вакууме наносится точно повторяющий рельеф непрозрачный слой серебра 4. Полученную пластинку осторожно приводят в контакт со второй оптически плоской стеклянной пластинкой 5, покрытой полупрозрачным слоем серебра 6. Зазор t между пластинами должен быть минимальным, поэтому обе пластины помещают в специальный зажим, который можно перемещать в плоскости, параллельной щели спектрального прибора (монохроматора) 7. Белый коллимированный свет через полупрозрачное зеркало 8 падает на интерферометр, где испытывает многократные отражения, после чего при помощи короткофокусной линзы 9 проецируется на входную щель монохроматора 7. Картина интерференции рассматривается в отраженном свете.
При скачкообразном изменении толщины воздушного зазора (за счет канала) интерференционная картина представляется в виде смещенных друг относительно друга систем линий РХП (рис. 6.3б). Величина смещения зависит от толщины измеряемого слоя. Таким образом, форма полос РХП воспроизводит (но в сильно увеличенном масштабе) форму воздушного зазора между пластинами интерферометра.
В соответствии с соотношением (6.13) используя обозначения, указанные на рис. 6.3, можно записать следующие условия образования линий РХП на пленке и в канале:
2t - (d1 / p)l= m l, (6.15)
2(t + d) - (d2 / p)l¢ = m¢l¢. (6.16)
Изменение фазы при отражении на границе воздух-серебро равно p - c, где c - малая величина. Пренебрегая дисперсией фазового скачка в области между l и l¢ можно считать, что (d1 / p)» (d2 / p)» 1. Тогда из соотношений (6.15) и (6.16) определяется толщина измеряемой пленки d:
d = (l¢m¢-lm) /2, (6.17)
где М = m + 1, M ¢ = m ¢ + 1. Интерференционные порядки m и m ¢можно определить, измерив длины волн линий РХП на пленке и в канале и записав условия образования экстремумов для каждой системы линий:
2 t - (d 1/ p) l 1= ml 1, 2 t - (d 1 /p) l¢ 1 = m¢l¢ 1, (6.18)
2 t - (d 1/ p) l 2= (m + 1) l 2, 2 t - (d1/p) l ¢2 = (m ¢ + 1) l ¢2. (6.19)
Из уравнений (6.18) и (6.19) определяем:
m = m + 1 = l 2/(l 1- l 2), (6.20)
m ¢ = m ¢+1 = l 2¢/(l 1¢- l 2¢). (6.21)
Значения m и m ¢, определенные по соотношениям (6.20) и (6.21), могут и не быть целыми вследствие дисперсии фазового скачка, их следует округлить до ближайшего целого.
Если толщина пленки мала (d < l /2), то интерференционные порядки ближайших друг к другу смещенных линий одинаковы, т.е. m = m ¢ и соотношение (6.17) будет иметь вид:
d = (l¢-l) m /2. (6.22)
Если толщина пленки d > l /2, интерференционные порядки ближайших друг к другу линий на пленке и в канале не будут одинаковыми. В таком случае толщину пленки определяют по формуле (6.17), а m и m ¢ по формулам (6.20) и (6.21).
Толщину пленок порядка нескольких длин волн можно определить или более грубыми методами (см. л.р. № 5), или, если это нужно сделать очень точно, - методом совпадений [17]. В этом случае толщину воздушного зазора между пластинами t можно подобрать такой, что линия длины волны m -порядка на пленке совпадет с линией m ¢-порядка в канале, т.е.
l = l¢. В соответствии с уравнением (6.17)
d = (m ¢- m) l /2. (6.23)
Формулы (6.17), (6.22) и (6.23) для определения толщины пленки получены при пренебрежении дисперсией d. Известно [16], что ошибка в определении толщины пленок, связанная с этим, для серебряных и алюминиевых высокоотражающих покрытий составляет 0,2 нм. Чтобы полностью исключить влияние дисперсии фазы, можно воспользоваться графическим методом определения толщины. В этом случае строятся графики зависимостей limi /2 и li¢mi ¢/2 (i = 1, 2,...) от l в соответствии с уравнениями (6.15) и (6.16).
Обе зависимости будут иметь одну и ту же форму, т.к. дисперсия фазового скачка для них одинакова. Толщину пленки можно вычислить как разность ординат построенных зависимостей.
Порядок выполнения работы.
1 Получение и измерение линий РХП.
1.1 Собрать установку, схема которой изображена на рис. 6.4. Спектральным прибором в данной схеме является монохроматор УМ-2. Пластинку с пленкой 1 (рис 6.4), толщину которой необходимо измерить, и оптическую пластинку 5, подготовленные к измерениям, поместить в зажим и осторожно поджать винты.
1.2 Перемещая держатель образца и линзу 9, добиться максимальной резкости интерференционной картины в поле зрения окуляра монохроматора. Важно, чтобы линии РХП на пленке и в канале были параллельны указателю монохроматора, острие которого должно совпадать с границей двух систем линий РХП (рис. 6.3а).
1.3 Измерить длины волн линий РХП на пленке и в канале во всей видимой области спектра (400-700 нм). Для этого совместить указатель монохроматора со спектральной линией и по цилиндрическому барабану найти номер деления, соответствующего данной линии. Полученные данные занести в таблицу. При измерении следует вращать барабан в направлении от больших делений к меньшим, чтобы избежать влияния на измерения механического люфта.
2 Обработка результатов измерений.
2.1 Определить длины волн в нм двух систем линий РХП (на пленке и в канале) с помощью градуировки, которая имеется на рабочем месте, или по интерполяционной формуле Гартмана [6]
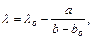
где b - деление барабана монохроматора, lо, a и b o - постоянные, определяемые экспериментально, их значения приведены на рабочем месте.
2.2 Определить порядки наблюдаемых линий по формулам (6.20) и (6.21). Полученные величины округлить до ближайшего целого значения.
2.3 Определить толщину пленки d по формуле (6.22) для всех наблюдаемых линий. Вычислить среднее арифметическое полученных значений и определить погрешность измерения.
2.4 Определить толщину пленки графическим методом. Для этого построить зависимости li m i/2 и li¢ m i¢/2 (i = 1, 2,..., n), где n - число измерений, от l. Разность ординат этих параллельных зависимостей дает значение толщины пленки в соответствии с соотношениями (6.15) и (6.16).
СПИСОК ЛИТЕРАТУРЫ
1 Сивухин Д.В. Общий курс физики. Оптика. - М., Наука, 1980.
2 Плетнева Н.А. Глазные болезни. - М., Медгиз, 1950.
3 Кривошеев М.И. и др. Цветовые измерения. М., Наука, 1990.
4 Апенко М.И., Дубовик А.С. Прикладная оптика. - М., Наука, 1982.
5 Базакуца В.А., Воинова Л.Г., Гнидаш Н.И. и др. Лабораторный практикум по физике ч.2 - Харьков, ХГУ, 1972.
6 Афанасьев В.А. Оптические измерения. - М., Недра, 1968.
7 Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. - М., Мир, 1980.
8 Ландсберг Г.С. Оптика. - М., Наука, 1976.
9 Шишловский А.А. Прикладная физическая оптика. - М., Физматгиз, 1961.
10 Рефрактометр УРЛ-1. Инструкция по эксплуатации.
11 Фарзане Н.Г. и др. Технологические измерения. - М. ВШ, 1989.
12 Описание и правила пользования оптическим пирометром ОППИР-017.
13 Борн М., Вольф Э. Основы оптики. М., Мир, 1970.
14 Комраков Б.М., Шапочкин Б.А. Измерение параметров оптических покрытий. - М., Машиностроение,1986.
15 Апенко М.И., Араев И.П. Оптические приборы в машиностроении. - Справочник. - М., Машиностроение, 1974.
16 Физика тонких пленок. Под ред. г. Хасса, Р.Э. Туна - т.IV.-М., Мир,1970.
17 Технология тонких пленок. Под ред. М. Майссела и Р. Глэнга. т.2.- М., Сов.радио, 1977.
18 Розенберг Г.В. Оптика тонкослойных покрытий. М., Физматгиз, 1958.
СОДЕРЖАНИЕ
Страница
Предисловие…………………………………………………………………….3
Лабораторная работа № 1 Изучение свойств зрения………………….…..…5
Лабораторная работа № 2 Микроскоп и его применение для визуаль-
ного оптического контроля…………….…...…..10
Лабораторная работа № 3 Использование рефрактометра УРЛ-1 для
контроля оптических параметров жидкости…..19
Лабораторная работа № 4 Оптическая пирометрия…………………...……25
Лабораторная работа № 5 Интерференционные измерения толщины
покрытий и шероховатости поверхности...……34
Лабораторная работа № 6 Измерение толщины тонких слоев при помо-
щи линий равного хроматического порядка…..41
Список литературы……………………..……………………………………..50
Навчальне видання
методичні вказівки
до лабораторних робіт з курсу
"оптичний контроль"
для студентів спеціальності 7.090903
"прилади неруйнівного контролю для технічної
та медичної діагностики"
Укладачі Сук Олександр Пилипoвич
Муссіл Володимир Вікторович
Лемешевська Катерина Тимофіївна
Меньшова Ірина Іванівна
Гнесь Наталія Олегівна
Пилипенко Валентина Володимирівна
Овчаренко Олександр Петрович
Відповідальний за випуск В.А. Базакуца
В авторській редакції
План 1999, поз.107
Підписано до друку 29.06.99. Формат 60´84 1/16. Папір Copy PAPIR
Друк – різографія. Умовн.-друк. арк. 1,8. Обл.-вид. арк. 1,85. Тираж 50 прим. Зам. № 965. Ціна договірна.
ХДПУ. 310002. Харків, вул. Фрунзе, 21.
ТОВ " Нова Ньюс ". 310153. Харків, пр. 50-річчя ВЛКСМ, 52.
