При исследовании влияния пяти факторов можно поставить не 16 опытов, а только 8, т. е. воспользоваться репликой 25-2. Здесь возможны двенадцать решений, если х 4 приравнять парному взаимодействию, а х 5 – тройному. Допустим, выбран вариант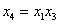 
и 
. Тогда определяющими контрастами являются 
и 
.
Если перемножить эти определяющие контрасты, то получится третье соотношение, задающее элементы столбца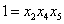 
. Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст.
.
Система смешивания определяется умножением обобщающего определяющего контраста последовательно на х 1, х 2, х 3 и т.д.
,
,
,
,
,
,
.
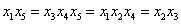Получается довольно сложная система смешивания линейных эффектов с эффектами взаимодействия первого, второго, третьего и четвертого порядков. Если, например, коэффициенты 
и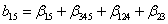 
отличаются от нуля, то возникают сомнения, можно ли пренебрегать другими парными взаимодействиями, с которыми смешаны линейные эффекты. Тогда следует поставить вторую серию опытов, выбрав нужным образом другую 1/4-реплику.
При этом можно воспользоваться методом «перевала». Смысл этого метода заключается в том, что вторая четверть-реплика получается из первой путем изменения всех знаков матрицы на обратные. Тогда в обобщающей определяющем контрасте тройные произведения имеют знак, противоположный их знаку в первой четверть-реплике. Тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов. Усредняя результаты обеих четверть-реплик, можно получить линейные эффекты, не смешанные с парными взаимодействиями.
Реплики большой дробности
При выборе 1/8-реплики 26-3 можно воспользоваться вектор-столбцами трех взаимодействий, например, так:
1. 
, 
, 
;
2. , 
, 
;
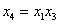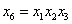3. , , ;
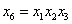4. , , .
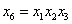Для каждого из этих решений можно сделать шесть перестановок. Итого получается 24 возможности выбора 1/8-реплики. Это при условии, что мы всюду выбираем положительные генерирующие соотношения.
Из четырех приведенных выше решений наименее удачно первое, поскольку все линейные эффекты смешиваются с парными взаимодействиями. Если априори известно, что из всех взаимодействий наиболее существенно х 1 х 2, то нужно выбрать второе решение, если х 1 х 3 – третье, а если х 2 х 3 – четвертое.
Допустим, мы избрали четвертое решение, предполагая, что из факторов х 4, х 5, х 6 наиболее существенным является х 4. Приравняем х 4тройному взаимодействию и запишем генерирующие соотношения
, 
, 
.
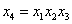имеем следующие определяющие контрасты:
, 
, 
.
Если попарно перемножить эти определяющие контрасты, то получим
, 
, 
.
Произведение трех определяющих контрастов равно
.
Чтобы полностью охарактеризовать разрешающую способность данной 1/8-реплики, запишем обобщающий определяющий контраст
.
Получается следующая система смешивания (эффекты выше второго порядка опущены):
,
,
,
,
,
.
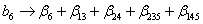Рассмотрим пример 1/16-реплики от 27.
1/16 часть от полного факторного эксперимента 27 дает возможность сократить число опытов до 8 вместо 128.
Выберем следующие генерирующие соотношения:
, , , 
.
Для них имеем следующие определяющие контрасты:
, 
, 
, 
.
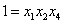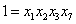Обобщающий определяющий контраст
Такой обобщающий определяющий контраст получен в результате попарного перемножения исходных контрастов, затем – умножения по три и по четыре.
Если всеми коэффициентами взаимодействия, начиная с тройных, можно пренебречь, то коэффициенты будут совместными оценками:
,
,
,
,
,
,
.
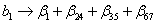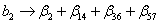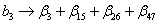Разрешающая способность такой реплики чрезвычайно мала, так как каждый линейный эффект определяется совместно с тремя парными взаимодействиями. Такой репликой можно пользоваться только в том случае, если все парные взаимодействия равны нулю. В большинстве случаев, начиная исследование процесса, трудно априорно предсказать, будут эффекты взаимодействия существенны или нет. Поэтому экспериментатор должен наметить план дальнейших опытов для случая, если парные эффекты значимы и поиск оптимальных условий будет неэффективным.
Матрицу планирования для этой реплики можно получить из первой реплики, изменив в ней все знаки на обратные. Такая реплика задается генерирующими соотношениями
, 
, 
, 
.
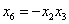В обобщающем определяющем контрасте все тройные произведения оказываются со знаком минус, и поэтому в совместных оценках для линейных эффектов не будет парных взаимодействий со знаком плюс. Усредняя результаты вычислений для таких двух реплик, можно получить раздельные оценки для всех линейных эффектов.
С ростом числа факторов увеличивается дробность реплик и усложняется система смешивания. Предельное число факторов для восьми опытов – семь. В этом случае оценивается восемь коэффициентов линейного уравнения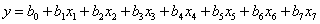 
и число степеней свободы равно нулю. При числе факторов от 9 до 15 приходится ставить 16 опытов. План с предельным числом факторов для данного числа опытов и заданной модели называется насыщенным. В этом случае число опытов равно числу оцениваемых коэффициентов. Все рекомендации для выбора системы смешивания аналогичны приведенным выше. Можно, далее, рассматривать построение дробных планов для числа факторов от 16 до 31 (при этом необходимо ставить 32 опыта), для числа факторов от 32 до 63 (здесь необходимы 64 опыта) и т. д.
