Выбор полуреплик. Генерирующие соотношения и определяющие контрасты

Дробный факторный эксперимент

Количество опытов в полном факторном эксперименте значительно превосходит число опре-деляемых коэффициентов линейной модели. Другими словами, полный факторный эксперимент об-ладает большой избыточностью опытов. Было бы заманчивым сократить их число за счет той инфор-мации, которая не очень существенна при построении линейных моделей. При этом нужно стремить-ся, чтобы матрица планирования не лишилась своих оптимальных свойств. Сделать это не так просто, но все же возможно. Итак, начнем поиск путей минимизации опытов.

Минимизация числа опытов

Начнем с самого простого – полного факторного эксперимента 2k. Запишем еще раз матрицу планирования.

№ опыта	x 0	x 1	x 2	(x 3) x 1 x 2	y
	+	–	–	+	y 1
	+	+	–	–	y 2
	+	–	+	–	y 3
	+	+	+	+	y 4

Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперт в виде неполного квадратного уравнения

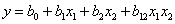
Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан ли­нейной моделью, то достаточно определить три коэффи­циента: b ₀, b ₁и b ₂. Остается одна степень свободы. Упот­ребим ее для минимизации числа опытов. При линейном приближении и вектор-столбец x ₁ x ₂ можно использовать для нового фактора x ₃. Поставим этот фактор в скобках над взаимодействием x ₁ x ₂ и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые мы имели в полном факторном эксперименте 2 ^k. Оценки смешаются следующим образом:

, .

Но нас это не должно огорчать. Ведь мы постулируем линейную модель, и, следовательно, все парные взаимодей­ствия незначимы. Главное, мы нашли средство минимизировать число опытов: вместо 8 опытов для изучения трех факторов оказывается можно поставить четыре! При этом матрица планирования не теряет своих оптимальных свойств (ортогональность, ротатабельность и т.п.). Найденное правило можно сформулировать так: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренеб­речь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.

Дробная реплика

Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной полного факторного эксперимента 2³ или «полурепликой». Если бы мы х ₃ приравняли к – x ₁ x ₂, то получили бы вторую по­ловину матрицы 2³. В этом случае , , . При реализации обеих полуреп­лик можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия, как и в полном факторном эксперименте 2³. Объединение этихдвух полуреплик и есть полный факторный эксперимент 2³. Матрица из восьми опытов для четырех факторного планирования будет полурепликой от полного фактор­ного эксперимента 2⁴, а для пятифакторного планиро­вания – четверть-репликой от 2⁵. В последнем случае два линейных эффекта приравниваются к эффектам взаимо­действия. Для обозначения дробных реплик, в которых p линейных эффектов приравнены к эффектам взаимо­действия, удобно пользоваться условным обозначением 2 ^k-p. Так, полуреплика от 2³ запишется в виде 2^3-1 а четвертьреплика от 2⁵ – в виде 2^5-2.

Выбор полуреплик. Генерирующие соотношения и определяющие контрасты

При построении полуреплики 2^3-1 существует всего две возможности: приравнять х₃ к + x ₁ x ₂или к – x ₁ x ₂. Поэтому есть только две полуреплики 2^3-1.

№ опыта	x 1	x 2	x 3	x 1 x 2 x 3
	+	+	+	+
	–	–	+	+
	+	–	–	+
	–	+	–	+

 

Для произведения трех столбцов первой матрицы выполняется соотношение: , а для второй матрицы: .

Символическое обозначение произведения столбцов, равного +1 или –1, называется определяющим контрастом. Контраст помогает определять сме­шанные эффекты. Для того чтобы определить, какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту. Так, если , то для x ₁ имеем

,

так как всегда . Для x ₂ находим

,

для x ₃

.

Это значит, что коэффициенты линейного уравнения будут оценками

,

,

.

Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением.

Полуреплики, в которых основные эффекты смешаны с двухфакторными взаимодействиями, носят название планов с разрешающей способностью III (по наибольшему числу факторов в определяющем контрасте).Такие планы принято обозначать: .

При выборе полуреплики 2^4-1 возможны восемь реше­ний:

 

1. ,

2. ,

3. ,

4. ,

5. ,

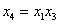6. ,

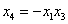7. ,

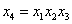8. .

 

Разрешающая способность этих полуреплик различна. Так, реплики 1–6 имеют по три фактора в определяющем контрасте, а 7–8 по четыре. Реплики 7 и 8 имеют максимальную разрешающую способность и называются главными. Разрешающая способность задается системой смешивания данной реплики. Она будет максимальной, если линейные эффекты смешаны с эффектами взаимодействия наибольшего возможного порядка.

При отсутствии априорной информации об эффектах взаимодействия экспериментатор стремится выбрать реплику с наибольшей разрешающей способностью, так как тройные взаимодействия обычно менее важны, чем парные. Если существует информация об эффектах взаимо­действия, то она должна использоваться при выборе реплики.

Реплики, в которых нет ни одного главного эффекта, смешанного с другим главным эффектом или парным взаимо­действием, а все парные взаимодействия смешаны друг с другом, носят название планов с разрешающей способ­ностью IV(по наибольшему числу факторов в определяю­щем контрасте). Они имеют обозначение .

Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей спо­собностью.

При выборе полуреплики 2^5-1 в распоряжении экспериментатора имеется множество вариантов.

Так, х ₅ можно приравнять к одному из 6 парных взаимодействий. В этом случае получим полуреплику с разрешающей способностью III. Очевидно, это будет не лучший выбор полуреплики. Далее, х ₅ можно приравнять к одному из четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями. И наконец, полуреплика может быть задана генерирующими соотношениями или 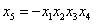. Определяющими контрастами в этом случае будут.

и .

Такие реплики носят название планов с разрешаю­щей способностью V и обозначаются .

Полурепликами 2^6-1 редко пользуются на практике. Ведь полуреплика 2^6-1 требует 32 опыта, а для экспериментатора выгодны планы 2^6-2 или 2^6-3 требую­щие соответственно 16 и 8 опытов. Поэтому с ростом числа факторов возрастает дробность применяемых реплик.

Заметим, что при построении главных полуреплик в определяющий контраст надо включать наибольшее число факторов.