1. Индивидуальный индекс - относительная величина, характеризующая изменение во времени каких-либо явлений и определяемая путем деления величины этого явления в отчетном периоде на величину его в базисном периоде.
В общем случае индивидуальный индекс цены определяется по формуле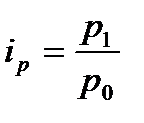 
, где 
и 
–цена продукции в отчетном и базисном периоде. В рассматриваемой задаче не известны цены товара, а дан процент изменения цен в отчетном периоде по сравнению с базисным, таким образом, индивидуальные индексы цен по видам товаров определяются по формуле:
,
где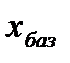 
- база сравнения, которая берется за 100%.
Для приведенного примера индивидуальные индексы цены по каждому виду продукции рассчитываются следующим образом:
яйцо - 
; мука - 
крупа -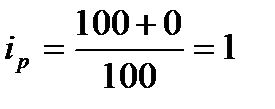 
.
2. Для обобщения относительного изменения показателя в сложной совокупности рассчитываются общие (сводные) индексы. Они характеризуют относительное изменение индексируемой величины в целом по всей совокупности, отдельные элементы которой несоизмеримы в физических единицах.
В зависимости от цели исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или среднюю.
При расчете общих индексов показатели, выраженные в различных единицах измерения, приводят к сопоставимому виду с помощью специальных коэффициентов взвешивания. При этом принято следующее соглашение:
− индексы количественных показателей (объема, площади, численности коров) используют в качестве весов значения базисного периода;
− индексы качественных показателей (цены, себестоимости, урожайности, надоя) – значения отчетного периода.
В данном случае для характеристики среднего изменения цен по всем товарам, в качестве веса используется объем проданной продукции в отчетном периоде (
), поэтому индекс цен определяется по формуле:
,
В примере исходными данными для расчета общего индекса цены являются данные о стоимости товара в отчетном периоде (
) и рассчитанные индивидуальные индексы цен по каждому товару (
).
В этом случае общий индекс цен как агрегатный определить нельзя, однако можно вычислить его по формуле среднего гармонического из индивидуальных индексов, который легко преобразовывается в формулу агрегатного индекса:
Следовательно, по всему ассортименту товаров цены в отчетном периоде снизились в среднем на 2,5 % (97,5%-100%=-2,5%) по сравнению с базисным.
Результаты проведенных расчетов удобно представить в табличном виде (таблица 9).
Таблица 9 Расчет индивидуальных и общего индексов цен
| Товар | Продано в фактических ценах, тыс. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % | Расчетные значения | |||
| базисный период, p0q0 | отчетный период, p1q1 | Индекс цены, 
| p0q1 | |||
| Яйцо | -10 | 0,90 | 266,67 | |||
| Мука | 1,05 | 209,52 | ||||
| Крупа | без изменений | 170,00 | ||||
| Итого | Х | Х | 646,19 | |||
| Общий индекс цен | 0,975 | |||||
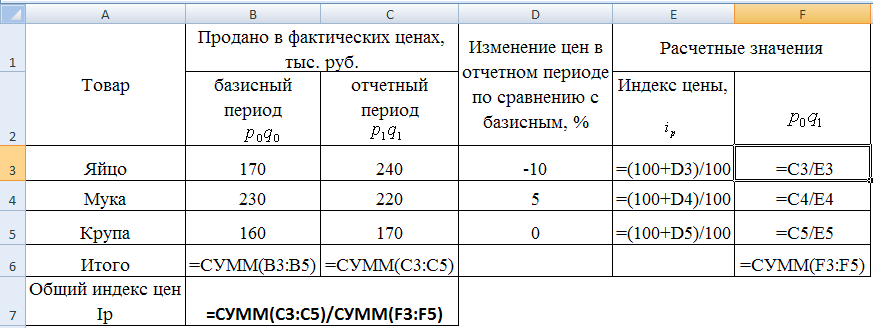
| На рис. 7 представлено проведение расчетов индивидуальных и общего индексов цены продаж по видам продукции в ТП Excel. | |||||
| ||||||
Рисунок 7 Расчет таблицы 9 в ТП Excel
3. Общий индекс изменения физического объема продукции, как показатель количественный, имеет вид:
Объем продаж в целом по всем видам продукции возрос на 15,4 %
4. Общий индекс товарооборота может быть рассчитан:
− по формуле агрегатного индекса, 
;
− по значениям общих индексов цен и физического объема: 
Товарооборот организации увеличился на 12,5 %.
5. Абсолютная величина изменения находится в виде разности числителя и знаменателя соответствующего индекса. Для определения изменения товарооборота, которое вызвано изменением цен на товары, следует рассматривать разность числителя и знаменателя формулы агрегированного индекса цены:
На основании полученного результата можно сделать вывод о том, что товарооборот в отчетном периоде снизился по сравнению с базисным на 16,19 тыс. руб. за счет изменения цен.
Тема 4. Ряды динамики
Процесс развития, движения общественных явлений во времени называется динамикой. Ряд динамики представляет собой значения статистических показателей, расположенные в хронологической последовательности.
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Они бывают цепными, базисными и средними.
Одно из направлений анализа ряда динамики – изучение закономерности изменения его уровней во времени. Тенденцию изменения показателей ряда динамики отражает линия тренда. Линия тренда позволяет построить прогноз развития явления на основе имеющихся статистических данных. Наиболее эффективным методом выявления тенденции развития является аналитическое выравнивание.
План изучения темы
1. Понятие и классификация рядов динамики. [1] c.145-146; [2] c.263-268; [3] c.214-217; [4] c.281-287; [6]; [7] с.323-326; [8]; [9] с.404-407.
2. Основные показатели изменения уровней ряда. [1] c.146-148; [3] c.217-221; [4] c.287-298; [6]; [7] с.331-344; [8]; [9] с.413-423.
3. Методы анализа основной тенденции в рядах динамики. [1] c.148-170; [2] c.283-304; [3] c.221-227; [4] c.298-318; [6]; [7] с.348-372; [8]; [9] с.425-453.
4. Технология выравнивания временных рядов в ТП Excel. [5] с.80-102; [10] с.231-262.
Задание 4
По приведенным в таблице 10 данным об объеме инвестиций по региону, определите следующие характеристики ряда динамики:
1) средние показатели ряда динамики;
2) недостающий уровень ряда за 2008 год;
3) цепные и базисные показатели;
4) прогнозный объем инвестиций в регион на 2010 и 2011 годы.
Таблица 10 Объем инвестиций в регион
| Год Показатель | |||||||||
Обозначение уровня ряда, 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
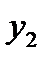
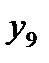
| Объем инвестиций, млн. руб. | 77,0 | 78,1 | 81,6 | 78,9 | 87,0 | 87,9 | 84,3 | 89,3 |
1. Средние показатели представляют собой обобщенные характеристики ряда динамики, с их помощью сравнивают интенсивность развития явления по отношению к различным объектам.
Основные средние показатели и их расчет представлен в таблице 11:
Таблица 11 Средние характеристики ряда динамики
| Показатель | Формула | Расчет |
| Абсолютный прирост |  ,
n –число уровней ряда
| 
|
| Коэффициент роста | 
| 
|
| Темп роста, (%) | 
| 
|
| Темп прироста, (%) | 
| 
|
|
| Для возведения в степень в табличном процессоре используется знак ^ (Shift+6). |
За период 2001-2009 гг. в среднем отмечается положительная динамика объема инвестиций: ежегодное увеличение составляет 1,54 млн.руб. или 1,9 %.
2. Восстановление недостающих промежуточных значений величины называется интерполяцией. Существует несколько способов восстановления, наиболее распространенными из которых являются следующие:
− по среднему абсолютному приросту: 
, где t –номер периода, значение которого восстанавливается;
− по среднему коэффициенту роста: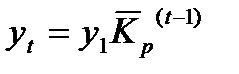 
.
Значение объема инвестиций в 2008 году, восстановленное по среднему абсолютному приросту рассчитывается следующим образом: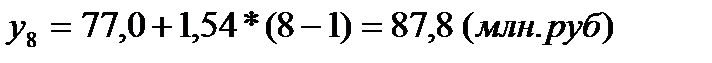 
3. Чтобы проследить за направлением и размером изменений уровней во времени для рядов динамики рассчитывается ряд цепных и базисных показателей.
Абсолютные показатели показывают, на сколько уровень одного периода больше или меньше уровня предшествующего периода, принятого за базу сравнения. Если значения цепных абсолютных изменений постоянны, то говорят о равномерном изменении ряда.
Относительные характеристики отражают интенсивность изменения в каждом отдельном периоде.
В таблице 12 представлены цепные и базисные показатели динамики для анализируемого ряда.
Таблица 12 Базисные и цепные показатели
| Показа-тель | Базисные | Цепные | ||||
| Формула | Расчет | Формула | Расчет | |||
| Абсолютный прирост | 
| Год | 
| 
| Год |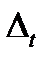 
|
| 78,1-77,0=1,1 | 78,1-77,0=1,1 | |||||
| 81,6-77,0=4,6 | 81,6-78,1=3,5 | |||||
| … | … | … | … | |||
| 89,3-77,0=12,3 | 89,3-87,8=1,5 | |||||
| Коэффициент роста | 
| Год | 
| 
| Год | 
|
| 78,1/77=1,014 | 78,1/77=1,014 | |||||
| 81,6/77=1,060 | 81,6/78,1=1,045 | |||||
| … | … | … | … | |||
| 89,3/77=1,160 | 89,3/87,8=1,017 | |||||
| Темп роста, (%) | 
| Год |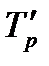 
| 
| Год | 
|
| 101,4 | 101,4 | |||||
| 106,0 | 104,5 | |||||
| … | … | … | … | |||
| 116,0 | 101,7 | |||||
| Темп прироста, (%) | 
| Год |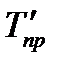 
| 
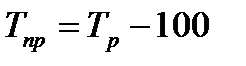
| Год | 
|
| 1,4 | 1,4 | |||||
| 6,0 | 4,5 | |||||
| … | … | … | … | |||
| 16,0 | 1,7 | |||||
| Абсолютное значение 1 % прироста | 
| Год | 
| 
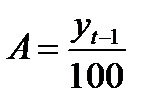
| Год | 
|
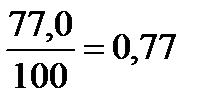
| 77,0/100=0,77 | |||||
| 78,1/100=0,781 | ||||||
| … | … | … | ||||
| 87,8/100=0,878 |
Произведенные расчеты показывают, что за исследуемый период объем инвестиций повысился на 12,3 млн.руб. или на 16 %. Рост объема инвестиций носит нестабильный характер, что подтверждается наличием отрицательных значений абсолютного цепного прироста и цепных темпов роста. Наибольший рост объема инвестиций отмечен в 2005[2] году.
4. Под прогнозом понимается научно обоснованное описание возможных состояний объектов в будущем. Процесс разработки прогнозов называется прогнозированием, или экстраполяцией.
Рассмотренные выше методы интерполяции могут применяться и в прогнозировании значений, но они имеют существенные недостатки, главный из которых заключается в том, что они учитывают лишь конечный и начальный уровни ряда, исключают влияния промежуточных уровней. Они могут быть использованы как приближенные, простейшие способы прогнозирования.
На практике для описания тенденции развития явления широко используются модели кривых роста, представляющие собой различные функции времени y = f(t). При таком подходе изменение исследуемого показателя связывают лишь с течением времени, считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.
|
| Трендовые модели строятся на основе диаграмм, представляющих уровни динамики с помощью контекстно-зависимого меню (рис 8). |
Рисунок 8 Построение линии тренда в ТП Excel
|
В результате открывается диалоговое окно «Формат линии тренда»[3], в котором содержаться различные трендовые модели: линейная, степенная, логарифмическая, полиномиальная, экспоненциальная.
Необходимо построить каждую из представленных моделей, оценить какая из них лучше описывает анализируемый ряд динамики. Для оценки качества модели необходимо дополнительно к линии тренда вывести на график показатель коэффициента детерминации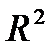 
. Коэффициент детерминации изменяется от 0 до 1, чем он ближе к единице, тем лучше линия тренда соответствует ряду динамики.
Результаты аналитического выравнивания объема инвестиций представлены в таблице 13.
Таблица 3 Результаты аналитического выравнивания
| Вид аналитического выравнивания | Коэффициент детерминации |
| Линейная | 0,793 |
| Экспоненциальная | 0,793 |
| Логарифмическая | 0,793 |
| Полиномиальная (2-го порядка) | 0,807 |
Наибольший коэффициент детерминации имеет полиномиальная линия тренда, т.е. 80,7% изменение объема инвестиций связано с изменением во времени, в 19,3% с другими факторами.
Если коэффициент детерминации имеет значение меньше 0,5, то это говорит о том, что к рассматриваемому ряду динамики нельзя применять аналитическое выравнивание, следовательно, построенная на его основании кривая роста не будет достоверно прогнозировать исследуемый процесс. В этом случае рекомендуется использовать сглаживание по скользящей средней.
Прогноз по полиномиальной модели представлен на рис. 9.
Рисунок 9 Прогнозирование объема инвестиций на 2010 и 2011 гг.
Как видно из приведенного графика, объем инвестиций к 2011 году достигнет 90 млн. руб.
