Будем теперь рассматривать бесконечную сумму вида 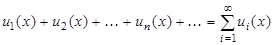 . Это выражение называется функциональным рядом. При различных значениях x из функционального ряда получаются различные числовые ряды
. Это выражение называется функциональным рядом. При различных значениях x из функционального ряда получаются различные числовые ряды 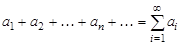 . Числовой ряд может быть сходящимся или расходящимся. Совокупность значений x, при которой функциональный ряд сходится, называется его областью сходимости.
. Числовой ряд может быть сходящимся или расходящимся. Совокупность значений x, при которой функциональный ряд сходится, называется его областью сходимости.
Числовой ряд называется сходящимся, если сумма n первых его членов 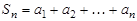 при
при 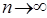 имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда
имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда  при неограниченном увеличении его номера стремится к нулю:
при неограниченном увеличении его номера стремится к нулю:  . Это необходимый признак сходимости для всякого ряда.
. Это необходимый признак сходимости для всякого ряда.
В случае бесконечной суммы будем вычислять ее с заданной точностью e. Cчитается, что требуемая точность достигается, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше чем е, то есть это слагаемое на результат практически не влияет. Тогда его и все последующие слагаемые можно не учитывать.
Пример. Написать программу для подсчета суммы  с заданной точностью е (е>0).
с заданной точностью е (е>0).
Указание по решению задачи. Рассмотрим, что представляет из себя заданный ряд:  . Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью e. Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения a1=-1,
. Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью e. Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения a1=-1, 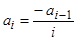 , а всю сумму - с помощью рекуррентного соотношения S0=0, Sn=Sn-1+an. (Данные рекуррентные соотношения выведите самостоятельно.)
, а всю сумму - с помощью рекуррентного соотношения S0=0, Sn=Sn-1+an. (Данные рекуррентные соотношения выведите самостоятельно.)
using System;
namespace Hello
{
class Program
{
static void Main()
{
Console.Write("Задайте точность вычислений е: ");
double e=double.Parse(Console.ReadLine());
double a=-1, s=0;
for (int i=2; Math.Abs(a)>=e; ++i)
{
s+=a; a/=-i;
}
Console.WriteLine("s={0:f2}",s);
}
}
}
Практическое задание
Замечание. При решении задач производить обработку следующих исключительных ситуаций: ввода пользователем недопустимых значений и переполнения при вычислении математических выражений.
I. Для заданного натурального n и действительного х подсчитать следующие суммы:
1)  ;
;
2) 
3) S = 1!+2!+3!+…+n!; 4)  .
.
II. Для заданного натурального k и действительного x подсчитать следующие выражения:
1)  2)
2) 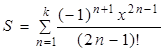
3) 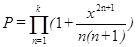 4)
4) 
III. Вычислить бесконечную сумму ряда с заданной точностью е (e>0).
1) 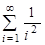 2)
2) 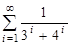 3)
3)  4)
4) 
IV. Вычислить и вывести на экран значение функции F(x) на отрезке [a,b] c шагом h=0.1 с точностью e. Результат работы программы представить в виде следующей таблицы:
| № | Значение x | Значение функции F(x) | Количество просуммированных слагаемых n |
| … |
Замечание. При решении задачи использовать вспомогательную функцию.
1. F(x) = 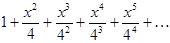 , x Î[0.1; 0.9].
, x Î[0.1; 0.9].
2. F(x) = 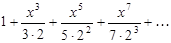 , x Î [0; 0.99].
, x Î [0; 0.99].
3. F(x)= 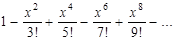 , x Î [0, 1].
, x Î [0, 1].
4. F(x) = 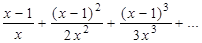 , x Î [1; 2].
, x Î [1; 2].






