При реакциях нулевого порядка скорость постоянна во времени
(3.64)
После интегрирования получаем
где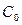 
– постоянная интегрирования, имеющая смысл начальной концентрации при 
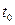=0.
Таким образом, в рассматриваемом случае концентрация реагента линейно убывает во времени.
Реакция первого порядка схематически представляется следующим образом:
Продукт реакции.
Кинетическое уравнение имеет вид:
(3.65)
а его решение 
показывает, что концентрация исходного компонента экспоненциально уменьшается во времени (рис. 3.2).
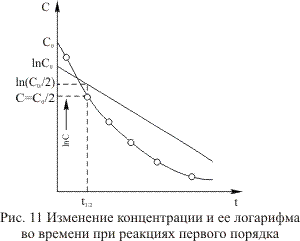
Решение этого уравнения можно представить и в другом виде, более удобном для определения константы скорости реакции. В результате разделения переменных и выбора пределов интегрирования
при 
=0
при температуре
получаем решение
из которого можно выделить, что 
линейно зависит от времени. Если опытные данные укладываются на прямую линию (см. рис. 3.2), то это указывает на первый порядок реакции. По углу наклона прямой определяется величина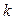 
.
Схема реакции второго порядка имеет вид
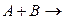Продукт реакции
или, например, 
, а скорость реакции описывается уравнением
(3.66)
которое при одинаковых концентрациях принимает вид
После разделения переменных и интегрирования соотношения
получаем соотношение
(3.67)
которое может быть использовано для определения 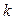. Если начальные концентрации реагентов неодинаковы и равны соответственно 
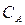и 
, а концентрация продукта в момент составляет 
, то получаем уравнение
логарифмирование которого дает
(3.68)
Все приведенные выше кинетические уравнения относятся к реакциям, протекающим только в прямом направлении, т. е. в условиях далеких от равновесия, что может, например, обеспечиваться за счет непрерывного отвода продуктов реакции. В общем случае может протекать и обратная реакция, тогда общая скорость для реакции вида равна
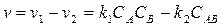(3.69)
По мере расходования реагентов 
и 
и образования продукта 
скорость прямой реакции 
уменьшается, а 
увеличивается. При 
суммарная скорость равна нулю, наступает равновесие. Тогда
или
(3.70)
т. е. константа равновесия 
равна отношению констант скоростей прямой и обратной реакции. В то же время соотношение (3.70) есть не что иное, как выражение закона действующих масс, полученное в данном случае через уравнение кинетики.
Связь между константой равновесия и константами скоростей прямой и обратной реакций
Признаки диффузионного лимитирования гетерогенной реакции---------
гетерогенных процессов. Эти процессы могут протекать на границах раздела фаз в однокомпонентных (жидкость – пар и т.д.) или в многокомпонентных (металл – шлак – куски извести и т. д.) системах.
Основные особенности процессов в диффузионной области: любой порядок процесса;
1) процесс первого порядка;
2) слабая зависимость скорости процесса от температуры и от величины поверхности раздела фаз;
3) резкое влияние на скорость процесса гидродинамических и аэродинамических условий процесса.
2 1---------Признаки кинетического лимитирования гетерогенной реакции---------
гетерогенных процессов. Эти процессы могут протекать на границах раздела фаз в однокомпонентных (жидкость – пар и т.д.) или в многокомпонентных (металл – шлак – куски извести и т. д.) системах.
Стадия, имеющая наибольшее сопротивление, является лимитирующей. Рассмотрим основные особенности процессов в кинетической области:
1) любой порядок процесса;
2) существенная зависимость скорости процесса от температуры по закону
k=Aexp(-E/RT)
3) зависимость скорости процесса от величины поверхности раздела фаз (степени дисперсности);
4) отсутствие влияния на скорость процесса изменений гидродинамических и аэродинамических условий процесса.
Уравнения теплопроводности для неподвижной и подвижной среды---------
Передача тепла в неподвижной среде описывается законом Фурье
(3.84)
где 
– тепловой поток (количество вещества, передаваемое через единицу поверхности в единицу времени);
– коэффициент теплопроводности.
С учетом конвекции закон Фурье можно представить в следующем виде:
(3.85)
где 
– теплоемкость при постоянном давлении;
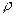– плотность среды;
– скорость потока.
