Что такое моделирование -------------------
Моделирование – воспроизведение характеристик некоторого объекта на другом материальном или мысленном объекте, специально созданном для их изучения. В этом определении моделирования по существу содержится также одно из общих определений модели. В настоящее время имеется целый ряд определений модели, ни одно из которых полностью не исчерпывает сущности этого понятия, видимо, из-за многообразия видов моделей и широкой области применения.
Что такое модель ----------------
Модель есть отражение существенных сторон реальной (или конструируемой) системы, в удобной форме представляющее информацию о ней. Здесь под системой понимается совокупность упорядоченных объектов, в которой каким-то образом определены цели. Все, что не входит в систему, является частью среды. Система характеризуется связями между входными и выходными сигналами, вид которых зависит от выбора границы между системой и средой. Отсюда можно сделать вывод, что вид модели системы в определенной мере зависит от точки зрения наблюдателя.
Расширяя понятие модели, можно отметить, что она не должна быть описанием фактического устройства системы, а может имитировать систему или «подражать» ее поведению, обладая при этом свойствами «расщепляемости» и «сопрягаемости», что дает возможность исследовать как характеристики отдельных элементов, так и их взаимодействие в системе.
Модели могут быть концептуальные (феноменологические, словесные), физические, математические. Модель должна создавать предпосылки для последующих решений (генерирования гипотез), поэтому информацию в ней целесообразно представлять в удобной для восприятия форме. Еще раз следует подчеркнуть, что модель есть упрощенное представление действительности; относительная простота модели – одна из главных ее характеристик.
Основные этапы моделирования ---------------------
Процесс моделирования можно представить в виде следующих этапов:
1. Постановка задачи.
2. Выбор и построение модели:
2.1. Структуризация – постановка гипотезы о внутренней структуре;
2.2. Математическое описание структурных блоков;
2.3.Составление вычислительного алгоритма;
2.4.Программирование, отладка и реализация программы на ЭВМ;
3. Исследование модели.
4. Перенос знаний с модели на оригинал, экспериментальная проверка модели.
На первом этапе необходимо четкое уяснение цели, учет априорных данных и, если необходимо, наблюдение, экспериментирование. Очень важным приемом является абстрагирование и выделение каких-либо сторон объекта, которые в данном случае наиболее целесообразно исследовать и описать.
На втором этапе, прежде всего, важно осознание общей структурной схемы модели. Здесь большую роль играют опыт, интуиция, профессионализм исследователя, т. е. знание конкретных особенностей объекта. При построении модели большую пользу может принести использование принципа аналогий.
Третий этап также является очень важным, так как при исследовании модели в случае достаточного приближения ее к действительности могут быть получены новые интересные результаты, например, найдены оптимальные сочетания параметров, ранее не наблюдавшиеся на объекте. Проверку соответствия модели и оригинала также целесообразно осуществлять именно в этих оптимальных или критических областях, поскольку они труднее всего поддаются адекватному отражению в модели.
Четвертый этап – экспериментальная проверка модели – очень тесно связан с двумя предыдущими. В процессе совершенствования модели приходится неоднократно переходить от одного этапа к другому и даже возвращаться, например, от последнего ко второму или третьему этапу.
Структурная схема познания объекта с помощью модели ----------------
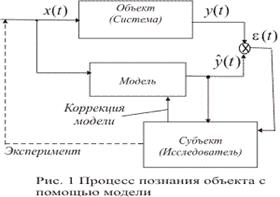 Процесс управления объектом с помощью модели можно рассматривать как процесс управления знанием или обучения модели (рис. 1.1). Исследователь, имея определённые знания об объекте, строит первый вариант модели
Процесс управления объектом с помощью модели можно рассматривать как процесс управления знанием или обучения модели (рис. 1.1). Исследователь, имея определённые знания об объекте, строит первый вариант модели  и путём сравнения с экспериментальными данными проверяет соответствие модели объекту. При необходимости ставятся специальные эксперименты и на основе анализа предсказанных
и путём сравнения с экспериментальными данными проверяет соответствие модели объекту. При необходимости ставятся специальные эксперименты и на основе анализа предсказанных 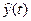 и фактических реакций объекта
и фактических реакций объекта 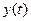 , корректируются параметры или структура модели.
, корректируются параметры или структура модели.
Изоморфизмы и гомоморфизмы ------------------
Изоморфизм и гомоморфизм – понятия, характеризующие соответствие между структурами объектов.
Изоморфизм (изоморфный – одинаковый по форме) есть взаимнооднозначное соответствие между двумя множествами каких-либо элементов или объектов. Пусть даны множества 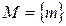 и
и 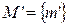 , а также множества отношений
, а также множества отношений 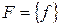 для
для 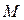 и
и  для
для 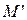 . Если между элементами множеств
. Если между элементами множеств 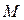 и
и 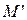 , а также между отношениями
, а также между отношениями  и
и 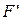 можно установить взаимнооднозначные соотношения
можно установить взаимнооднозначные соотношения  ,
, 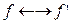 , такие, что из выполнения соотношений
, такие, что из выполнения соотношений  для каких-либо элементов множества
для каких-либо элементов множества 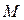 следует выполнение соотношений
следует выполнение соотношений  для соответствующих элементов множества
для соответствующих элементов множества 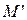 и обратно, то множества
и обратно, то множества 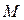 и
и 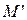 изоморфны, т. е. при изоморфизме сохраняется система соотношений
изоморфны, т. е. при изоморфизме сохраняется система соотношений  . Всякому свойству множества
. Всякому свойству множества 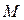 соответствует аналогичное свойство множества
соответствует аналогичное свойство множества 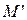 . Полный изоморфизм может быть лишь между геометрической фигурой и ее аналитическим выражением в виде формулы. Однако, учитывая, что изоморфизм связан не со всеми, а лишь с некоторыми фиксированными в познавательном смысле свойствами, можно за счет выбора соответствующих структурных элементов получить близкие к изоморфным отношения и для реальных объектов.
. Полный изоморфизм может быть лишь между геометрической фигурой и ее аналитическим выражением в виде формулы. Однако, учитывая, что изоморфизм связан не со всеми, а лишь с некоторыми фиксированными в познавательном смысле свойствами, можно за счет выбора соответствующих структурных элементов получить близкие к изоморфным отношения и для реальных объектов.
Гомоморфизм (гомоморфный – подобный по форме) отличается от изоморфизма тем, что соответствие между множествами 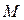 и
и 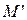 не взаимнооднозначно, один элемент множества
не взаимнооднозначно, один элемент множества 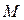 может соответствовать многим элементам множества
может соответствовать многим элементам множества 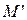 . Примером гомоморфной модели является географическая карта по отношению к местности, замена небесного тела материальной точкой, представление динамики изменения содержания углерода или температуры металла в сталеплавильной ванне в виде траектории движения точки во времени (модель с сосредоточенными параметрами). В отличие от этого модель с распределенными параметрами, учитывающая граничные условия и распределение физических свойств металлической ванны не только во времени, но и в пространстве, находится в большем соответствии с принципами изоморфизма.
. Примером гомоморфной модели является географическая карта по отношению к местности, замена небесного тела материальной точкой, представление динамики изменения содержания углерода или температуры металла в сталеплавильной ванне в виде траектории движения точки во времени (модель с сосредоточенными параметрами). В отличие от этого модель с распределенными параметрами, учитывающая граничные условия и распределение физических свойств металлической ванны не только во времени, но и в пространстве, находится в большем соответствии с принципами изоморфизма.
Формулировка первой теории подобия -----------
Первая теорема. Явления, подобные в том или ином смысле (физически, математически, кибернетически и т. д.), имеют некоторые одинаковые сочетания параметров, называемые критериями (числами) подобия.
Формулировка второй теории подобия -----------
Вторая теорема. Известна под названием 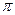 -теоремы. Она гласит: всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено зависимостью между числами подобия, т. е. уравнением, связывающим безразмерные величины, полученные из участвующих в процессе параметров.
-теоремы. Она гласит: всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено зависимостью между числами подобия, т. е. уравнением, связывающим безразмерные величины, полученные из участвующих в процессе параметров.
8--- Дополнительное положение о подобии сложных систем и принцип прямой аналогии –
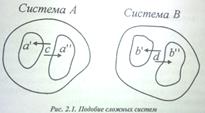 Подобие сложных систем
Подобие сложных систем 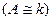 , состоящих из нескольких подсистем, соответственно подобных в отдельности
, состоящих из нескольких подсистем, соответственно подобных в отдельности 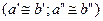 , обеспечивается подобием всех сходственных элементов, являющихся общими для подсистем
, обеспечивается подобием всех сходственных элементов, являющихся общими для подсистем
Краткое сопоставление структурно-математического и элементно-физического подхода к моделированию -----------
Нарисовать схемки примеров тепловой, гидравлической и электрической аналогии-

11- ----Первый закон термодинамики и его конкретные реализации в зависимости от вида взаимодействия между системой и средой (кратко формулы и ограничения)
Первый закон термодинамики
Первый закон термодинамики (закон сохранения энергии для тепловых процессов) определяет количественное соотношение между изменением внутренней энергии системы дельта U, количеством теплоты Q, подведенным к ней, и суммарной работой внешних сил A, действующих на систему.
Первый закон термодинамики - Изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теплоты, подведенного к системе извне, и работы внешних сил, действующих на нее:

Первый закон термодинамики - количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
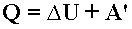
Частные случаи первого закона термодинамики для изопроцессов
При изохорном процессе объем газа остается постоянным, поэтому газ не совершает работу. Изменение внутренней энергии газа происходит благодаря теплообмену с окружающими телами:

При изотермическом процессе количество теплоты, переданное газу от нагревателя, полностью расходуется на совершение работы:
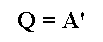
При изобарном расширении газа подведенное к нему количество теплоты расходуется как на увеличение его внутренней энергии и на совершение работы газом:

Адиабатный процесс - термодинамический процесс в теплоизолированной системе.

Теплоизолированная система - система, не обменивающаяся энергией с окружающими телами.
Формула КПД теплового двигателя:
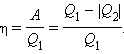
Здесь Q1 - количество теплоты, полученное рабочим телом,
Q2 - количество теплоты, отданное холодильнику.
A - полезная работа.
Формула Карно для оценки максимального КПД теплового двигателя:
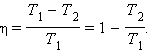
T1 - температура нагревателя, T2 - температура холодильника.






