ЧАСТЬ 1
1–10. Даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
1. А (–5; 0), В (7; 9), C (5; –5).
2. A (–7; 2), B (5; 11), С (3; –3).
3. А (–5; –3), В (7; 6), C (5; –8).
4. А (–6; –2), В (6; 7), C (4; –7).
5. А (–8; –4), В (4; 5), C (2; –9).
6. А (0; –1), В (12; 8), С (10; –6).
7. А (–6; 1), В (6; 10), С (4; –4).
8. А (–2; –4), В (10; 5), С (8; –9).
9. А (–3; 0), В (9; 9), С (7; –5).
10. А (–9; –2), В (3; 7), С (1; –7).
11–20. Решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21–30. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31–40. Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 
41–50. Даны координаты точек А, В, С и М.
Найти: 1) уравнение плоскости Q, проходящей через точки А, В и С; 2) канонические уравнения прямой, проходящей через точку М перпендикулярно плоскости Q; 3) точку пересечения полученной прямой с плоскостью Q; 4) расстояние от точки М до плоскости Q.
41. А (- 3; - 2; - 4), В (- 4; 2; - 7), С (5; 0; 3), М (- 1; 3; 0)
42. А (2; - 2; 1), В (- 3; 0; - 5), С (0; - 2; - 1), М (- 3; 4; 2)
43. А (3; 6; - 2), В (0; 2; - 3), С (1; - 2; 0), М (- 7; 6; 6)
44. А (5; 4; 1), В (- 1; - 2; - 2), С (3; - 2; 2), М (- 5; 5; 4)
45. А (1; - 4; 1), В (4; 4; 0), С (-1; 2; - 4), М (- 9; 7; 8)
46. А (4; 6; - 1), В (7; 2; 4), С (- 2; 0; - 4), М (3; 1; - 4)
47. А (0; 6; - 5), В (8; 2; 5), С (2; 6; - 3), М (5; 0; - 6)
48. А (- 2; 4; - 6), В (0; - 6; 1), С (4; 2; 1), М (7; - 1; - 8)
49. А (- 4; - 2; - 5), В (1; 8; - 5), С (0; 4; - 4), М (9; - 2; - 10)
50. А (3; 4; - 1), В (2; - 4; 2), С (5; 6; 0), М (11; - 3; - 12)
51-60. Туристской фирме требуется не более а трехтонных автобусов и не более в пятитонных автобусов. Отпускная цена автобусов первой марки 20000 у.е., второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более с у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной. Решить задачу графическим методом.
51. а = 11 в = 9 с = 460000
52. а = 12 в = 10 с = 520000
53. а = 13 в = 11 с = 580000
54. а = 14 в = 12 с = 640000
55. а = 15 в = 13 с = 700000
56. а = 16 в = 14 с = 760000
57. а = 17 в = 15 с = 820000
58. а = 18 в = 16 с = 880000
59. а = 19 в = 17 с = 940000
60. а = 20 в = 18 с = 1000000
ЧАСТЬ 2
61-70. Исследовать функцию y = f (x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f (x) на отрезке [ a, b ].
61.  a = - 1, b = 3
a = - 1, b = 3
62.  a = - 1, b = 2
a = - 1, b = 2
63.  a = 2, b = 3
a = 2, b = 3
64.  a = - 1, b = 2
a = - 1, b = 2
65.  a = 0, b = 4
a = 0, b = 4
66.  a = - 2, b = 3
a = - 2, b = 3
67.  a = - 3, b = 0
a = - 3, b = 0
68.  a = -3, b = 1
a = -3, b = 1
69.  a = 1, b = 4
a = 1, b = 4
7 0.  a = - 1, b = 4
a = - 1, b = 4
71-80. Найти неопределённые интегралы и результат интегрирования (в одном примере) проверить дифференцированием.
71. a)  б)
б) 
в) 
72. а)  б)
б) 
в) 
73. а)  б)
б) 
в) 
74. а)  б)
б) 
в) 
75. а)  б)
б) 
в) 
76. а)  б)
б) 
в) 
77. а)  б)
б) 
в) 
78. а)  б)
б) 
в) 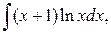
79. а)  , б)
, б) 
в) 
80. а)  б)
б) 
в) 
81-90. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.
81. 

82. 
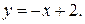
83. 

84. 

85. 

86. 

87. 

88. 

89. 

90. 

91-100. Задачи по теории вероятностей.
- В читальном зале имеется 6 учебников по теории вероятностей, из них 3 в мягком переплёте. Библиотекарь взял 2 учебника. Найти вероятность того, что оба учебника окажутся в мягком переплёте.
- Студент знает ответы на 20 вопросов из 25 программных вопросов. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором 3 вопроса.
- Для некоторой местности в июле шесть пасмурных дней. Найти вероятность, что первого и второго июля будет ясная погода.
- Из 200 рабочих не выполняют норму выработки 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
- Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0.6, вторым – 0.7, третьим – 0.8. Найти вероятность того, что при одном выстреле попадут в цель: а) все три стрелка; б) попадёт хотя бы один из них.
- В ящике лежат 20 электрических ламп, из которых 2 нестандартные. Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
- Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечётное число очков.
- В урне находится 15 шаров, 5 из них красные, а остальные белые. Наугад друг за другом извлекают три шара. Найти вероятность того, что все они окажутся красными.
- В бассейне находятся 25 карпов и 5 лещей. Наудачу вылавливают 3 рыбы. Найти вероятность того, что среди них будет хотя бы один лещ.
100. В офис турфирмы пришли 3 клиента. Вероятность приобрести тур у каждого клиента равна 0.4. Найти вероятность того, что: 1) все клиенты приобретут туры; 2) ни один из них тур не приобретёт.
101 – 110. Задана дискретная случайная величина Х:
| Х | k | k + 1 | k + 2 | K + 3 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
(k – номер варианта студента)
Найти: а) математическое ожидание М(х); б) дисперсию D (x); в) среднее квадратическое отклонение б(х).
Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике (1 часть или 2 часть) студента ФИО заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.
Примеры решения и оформления заданий приведены в учебно-методических пособиях [8], [9].
Критерии для оценки контрольной работы:
1. Наличие разумных пояснений к выполняемым пунктам задания
2. Указание используемых формул
3. Соблюдение рекомендованного алгоритма решения задания
4. Точность вычислений
5. Решение всех указанных задач.
Перечень вопросов для подготовки к зачётуЧасть 1
1. Декартовы координаты на плоскости. Координаты двух точек, симметричных относительно а) оси Ox, б) оси Oy, в) начала координат
2. Расстояние между двумя точками
3. Деление отрезка в данном отношении. Координаты середины отрезка
4. Определение линии на плоскости
5. Прямая на плоскости. Уравнение прямой с угловым коэффициентом
6. Общее уравнение прямой
7. Угол между прямыми
8. Условия параллельности и перпендикулярности прямых
9. Уравнение прямой, проходящей через заданную точку в заданном направлении
10. Уравнение прямой, проходящей через две заданные точки
11. Уравнение окружности
12. Определители второго порядка
13. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения
14. Методы вычисления определителей третьего порядка
15. Решение систем двух линейных уравнений с двумя неизвестными методом Крамера
16. Решение систем трех линейных уравнений с тремя неизвестными методом Крамера
17. Матрицы. Сложение и умножение матриц
18. Обратная матрица и ее вычисление
19. Решение системы линейных уравнений с помощью обратной матрицы
20. Геометрическая интерпретация системы линейных неравенств
21. Графический метод решения задачи линейного программирования
22. Векторы. Действия над ними. Скалярное произведение векторов.
23. Общее уравнение плоскости и его исследование.
24. Уравнение плоскости, проходящей через три данные точки.
25. Условия параллельности и перпендикулярности плоскостей.
26. Расстояние от точки до плоскости.
27. Прямая в пространстве. Канонические уравнения прямой.
28. Условия параллельности и перпендикулярности прямой и плоскости.
Формат и содержание зачёта, критерии оценки.
Зачёт проводится в установленное расписанием время по утвержденным билетам. Билет содержит два теоретических вопроса и одно практическое задание. Практическое задание оформляется в письменном виде со всеми необходимыми комментариями по алгоритму решения. На теоретические вопросы студент отвечает устно. Для получения оценки «Зачтено» необходимо правильно решить практическое задание, знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента.
Перечень вопросов для подготовки к экзамену Часть 2
1. Основные элементарные функции их свойства и графики.
2. Определение производной функции в точке. Таблица производных.
3. Производная сложной функции.
4. Промежутки возрастания и убывания функции. Максимум и минимум функции.
5. Наибольшее и наименьшее значения функции на отрезке.
6. Первообразная. Неопределенный интеграл. Таблица интегралов.
7. Определение и свойства определенного интеграла.
8. Геометрический смысл определенного интеграла.
9. Формула Ньютона–Лейбница.
10. Вычисление площадей плоских фигур с помощью определенного интеграла.
11. Ряды. Необходимый признак сходимости ряда.
12. Дифференциальные уравнения первого порядка.
13. Классическое и статистическое определения вероятности события.
14. Теоремы сложения вероятностей.
15. Теоремы умножения вероятностей.
16. Формула Бернулли.
17. Случайные величины дискретные и непрерывные.
18. Математическое ожидание и дисперсия дискретной случайной величины.
19. Вариационный ряд. Статистическое распределение выборки.
20. Полигон частот.
21. Гистограмма частот.
22. Основные типы систем массового обслуживания.
23. Простейший поток заявок и его свойства.
Формат и содержание экзамена, критерии оценки. Экзамен проводится в установленное расписанием время по утвержденным билетам. Билет содержит два теоретических вопроса и одно практическое задание. Практическое задание оформляется в письменном виде со всеми необходимыми комментариями по алгоритму решения. На теоретические вопросы студент отвечает устно. Для получения оценки «Отлично» необходимо правильно решить практическое задание, знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Хорошо» необходимо знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Удовлетворительно» необходимо уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы Перечень рекомендуемой литературы
Основная литература:
1. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике (в двух частях) – М.: Финансы и статистика, 2005.
2. Шипачев В.С. Основы высшей математики. – М.: Высшая школа, 2006.
3. Краснов М.А. и др. Вся высшая математика (в шести томах). – М.: Эдиториал УРСС, 2000.
4. Кремер Н.Ш. и др. Высшая математика для экономистов. – М.: ЮНИТИ, 2002.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2006.
Дополнительная литература:
6. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов. – М.: ЮНИТИ, 2002.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 2006.
8. Коровина Л.А. Математика (Элементы аналитической геометрии, линейной алгебры и линейного программирования): Методическое пособие по изучению курса и выполнению расчетных работ для студентов, обучающихся по специальности «Туризм». – М.: МАТГР, 2007.
9. Коровина Л.А. Математика (дифференциальное и интегральное исчисления). Учебно-методическое пособие по изучению курса и выполнению расчётных работ. М.: МГИИТ, 2010.-32 с.






