1. Задача дисперсионного анализа. Во многих областях практической
деятельности встречаются объекты исследования, состояние которых определяется факторами, не имеющими количественного описания.
Например, рассматривается процесс измерения какой-либо физической
величины рядом операторов параллельно нескольким приборам (или нескольким методам); причем каждый оператор измеряет эту величину всеми приборами (методами). Средние значения наблюдаемой величины, полученные операторами, отличаются друг от друга. Эти различия средних значений может быть связано со случайной погрешностью, систематической приборной (методической) ошибкой и влиянием оператора.
Требуется определить, насколько существенно влияние на результат
измерения двух факторов: прибора (метода) и оператора.
Аналогичная задача возникает при использовании радиодеталей из нескольких партий, при этом надо определить существенно ли отличаются параметры деталей различных партий. Итак, для изучения влияния факторов, не имеющих количественного описания, на исследуемую величину применятся метод дисперсионного анализа.
2. Однофакторный дисперсионный анализ. В общем виде задача однофакторного дисперсионного анализа ставится следующим образом. Пусть наблюдают m независимых случайных величин x1, x2,... xi... xj, аспределенных нормально с центрами mx1,mx2,... mxm и неизвестной, но одинаковой для всех x i дисперсией, b2.
Пусть над каждыми переменными x i производится серия из n наблюдений. Данные i -ой серии следующие:
xi1, xi2,...xij,...xin (i= 1, 2 ,...m; j= 1, 2 ...n).
Опираясь на эти статистические данные требуется роверить нуль – гипотезу (Н0) о равенстве математических ожиданий
mx1=mx2=...mxm.
Если проверяемая гипотеза верна, то сопоставление средних
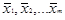 в каждой серии не должно дать значимого расхождения между ними. И наоборот, если такое расхождение обнаружено, то нулевую гипотезу следует отбросить.
в каждой серии не должно дать значимого расхождения между ними. И наоборот, если такое расхождение обнаружено, то нулевую гипотезу следует отбросить.
Возвращаясь к рассмотренному примеру, положим, что число
операторов равно m и каждый из них производит n замеров некоторой физической величины x (табл.1).
Каждая серия из n измерений xi1, xi2,... xin (i =1,2,... m) представляет
собой выборку объема n из генеральной совокупности измерений отдельного оператора xi (i =1,2 ,...m).
Итак, общее число измерений величины xij (i =1,2,... m – номер оператора, j =1,2 ,...n – номер измерения) равно mn.
ТАБЛИЦА1
| № оператора № измерений | x1 | x2 | ... | Xj | ... | |
| . . . j . . . n | x11 x12 x1j x1n | x21 x22 x2j x2n | Xj1 xi2 xij xin | xm1 xm2 Xmn | ||
| Среднее значение в серии | x1 | x2 | Xi | Xm | ||
| Общее среднее |
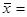
|
Среднее арифметическое из n измерений i – го оператора обозначим через xi
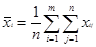
 (1)
(1)
Обозначим через 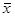 общее среднее арифметическое значение всех mn измерений –
общее среднее арифметическое значение всех mn измерений –
 (2)
(2)
Все наблюдаемые значения x ij образуют выборку объемом mn из
генеральной совокупности x, имеющей также нормальное распределение с центром mx и дисперсией σ2 Очевидно, что значение
x (2) является оценкой математического ожидания mx по данным выборки.
Согласно методу однофакторного дисперсионного анализа надо
сумму квадратов отклонений значений от общего среднего Q0 разложить на составные части, одна из которых соответствует фактору
изменчивости – Qf (здесь: оператор), другая – QR –влиянию случайных причин (здесь: приборы или методы).
При этом указанные суммы находят по формулам:
 2 (3)
2 (3)
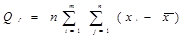 2 (4)
2 (4)
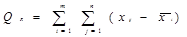 2 (5)
2 (5)
Известно [1], что
Q0 = Qf +QR (6)
Итак, величина Q0 представляет собой сумму квадратов отклонений
наблюдаемых значений x от общего среднего 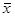 и называется “общей” или “полной” суммой квадратов.
и называется “общей” или “полной” суммой квадратов.
Величина Qf это сумма квадратов отклонений средних по группам (сериям) 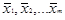 от общего среднего
от общего среднего 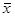 , она называется суммой квадратов отклонений между группами. QR является суммой квадратов отклонений значений xi j от средних
, она называется суммой квадратов отклонений между группами. QR является суммой квадратов отклонений значений xi j от средних  , в группах и называется сумой квадратов внутри групп (серий).
, в группах и называется сумой квадратов внутри групп (серий).
В практических расчетах обычно вычисляют только общую сумму Q0
и сумму квадратов между группами Qf, сумму квадратов внутри групп получают по формуле (6):
QR = Q0 -Qf (7)
и поэтому её называют “остаточной” суммой.
Суммы квадратов Q0,Qf,QR, деленные на соответствующие числа
степеней свободы ν1= mn -1, νF = m -1, νR = m (n -1), дадут три несмещенные оценки дисперсии σ2 в общей выборке x:
S02 = 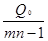 - общая оценка дисперсии (8)
- общая оценка дисперсии (8)
SF2 = 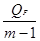 - оценка дисперсии между группами (9)
- оценка дисперсии между группами (9)
SR2 =  - оценка дисперсии внутри групп (10)
- оценка дисперсии внутри групп (10)
Выполнение дисперсного анализа заключается в сравнивании
оценки SF 2 дисперсии, вызванной изучаемым фактором изменчивости F, и оценкой достаточной дисперсии SR 2, имеющей место уже после того, как влияние фактора F было устранено (т.е. обусловленной исключительно случайными факторами – погрешностью измерений).
Если нуль-гипотеза о равенстве центров распределения верна,
mx1=mx2=...mxm, (11)
то оценки дисперсий SF 2 и SR 2 должны различаться между собой лишь случайно. Проверка данной гипотезы выполняется по критерию Фишера. Для этого находят F – отношение и сравнивают величину F с предельным значением Fт, которое находят по таблице F – распределения при степенях свободы νF = m -1 и νR= m (n -1), α = 0,05[2,3].
В случае
F < Fт (12)
расхождения между оценками SF2 и SR2 несущественны (с вероятностью p 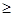 0,05). Это означает, что нуль-гипотеза подтверждается. Исследователь может считать опытные данные однородными – это означает, что фактор изменчивости не оказывает существенное влияние на среднее значение измеряемых величин в группах.
0,05). Это означает, что нуль-гипотеза подтверждается. Исследователь может считать опытные данные однородными – это означает, что фактор изменчивости не оказывает существенное влияние на среднее значение измеряемых величин в группах.
При
F > Fт (13)
следует, что фактор изменчивости оказывает существенное влияние на данные измерений в группах. Влияние фактора изменчивости значимо.
Порядок выполнения работы.
1. Получить у преподавателя данные нескольких выборок случайной
величины x.
2. Данные выборок представить в виде таблицы 1.
3. Вычислить среднее значение в сериях 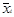 (i=1,2,… m) и общее
(i=1,2,… m) и общее
среднее 
4. Определить значение сумм квадратов QR,Q0,Qf
Для удобства вычислений рекомендуется перейти к новым переменным yij по формуле
yij = xij -  , (14)
, (14)
где 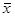 - ближайшее к общему среднему целое число.
- ближайшее к общему среднему целое число.
При таком преобразовании переменных формул для сумм квадратов
примут следующий вид:
 2=
2= 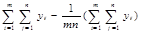 2+
2+  (15)
(15)
 2=
2= 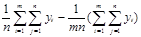 2=
2= 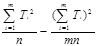 ;(16)
;(16)
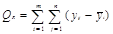 2=
2= 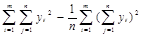 =
= 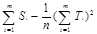 (17)
(17)
В формулах (15), (16), (17) введены следующие обозначения:
Si = 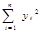 ; Ti =
; Ti = 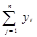 .
.
Результаты вычислений представляют в виде таблицы 2.
ТАБЛИЦА 2
.
| Номер испытаний (j) | Фактор изменчивости | ||||||
| 1- ый оператор | 2- ой оператор | … | m - ый оператор | ||||
| y1j | y1j2 | y2j | y2j2 | ymj | ymj2 | ||
| . . . n | |||||||
| si | S1 | s2 | sm | 
| |||
| ti | t1 | t2 | tm | 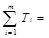
| |||
| ti2 | t12 | t22 | tm2 | 
|
Затем по формуле (15), (16) с помощью полученных сумм
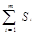 ,
, 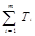 ,
, 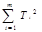
находят величины Q0,Qf . Остаточную сумму квадратов QR вычисляют по формуле
QR = Q0 -Qf
5. Полученные степени свободы ν0, νF, νR по формулам:
ν0= mn -1
νF = m -1
νR = m (n -1)
6. Вычислить несмещенные оценки S02, SF2, SR2
S02 = 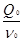 ;
;
SF2 = 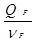 ;
;
SR2 = 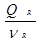 ;
;
7. Подсчитать значение F - отношения
F = 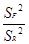 .
.
При формировании F - отношения в числителе ставится большая из двух оценок дисперсий, т.е. в нашем случае SF2 > SR2
8. Найти из таблицы F – распределения случайной величины [2,3]
предельное значение Fт, соответствующее уровню значимости α = 0,05 и степеням свободы νF и νR.
9.Сравнить полученное значение F (n.7) с табличными FT и сделать заключение о проверяемой нуль-гипотезе Н0. Если F £ FTабл,то гипотеза принимается.
Пример:
Определить, однородны ли результаты измерения напряжения (в вольтах), тремя операторами при использовании измерительных приборов различных типов. Результаты измерений даны в таблице 3.
ТАБЛИЦА 3
| Номер Измерений (j) | 1-ый оператор | 2-ой оператор | 3-ий оператор |

| |||
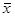 = 222 = 222
|
ТАБЛИЦА 4
.
| Номер измерений (j) | 1- ый оператор | 2- ой оператор | 3- ий оператор | ||||
| y1j | y1j2 | y2j | y2j2 | y3j | y3j2 | ||
| -1 | -10 | ||||||
| -8 | |||||||
| -2 | |||||||
| Si | 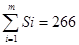
| ||||||
| Ti | -20 | 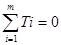
| |||||
| Ti2 | 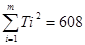
|
В таблице 4 показаны промежуточные вычисления, позволяющие
очень просто найти суммы квадратов QR, Q0, Qf:
Q0 =  = 226 – 0 = 226;
= 226 – 0 = 226;
QF =  =
= 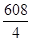 -0 = 152;
-0 = 152;
QR = Q0 -Qf = 268 – 152 =114.
Оценки дисперсии при этом:
SF2 = 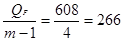 ;
;
SR2 = 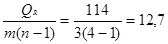 ;
;
F – отношение примера равно;
F = 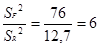
Табличное значение F – отношения:
Fт = 4,26 при α = 0.05, ν F = m -1, ν R = m (n -1) = 9
Так как
F = 6 > Fт = 4.26,
то считают измерения неоднородными, т.е. Фактор изменчивости (оператор) играет существенную роль в расхождении средних значений показаний приборов.
Контрольные вопросы.
1. Что называется фактором изменчивости и случайности?
2. Какого типа практические задачи обычно решаются методом
дисперсионного анализа?
3. Как математически формируется задача однофакторного анализа?
4. Как формируются оценки дисперсий (общей, между сериями,
остаточная)? Разброс каких случайных величин они характеризуют?
5. В чем заключается F – критерий Фишера?
Литература.
1. Круг Г.К. Статические методы в инженерных исследованиях:
Лабораторный практикум. Бородюк В.П. и др.- М.: В.Ш.,1983.
2. Венцель Е.С. Теория вероятностей. - М.: В.Ш., 1983
3. Гмурман В.С. Теория вероятностей и математическая
статистика. – М.: В.Ш., 1972.
Лабораторная работа № 3.






