ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА «ЭЛЕКТРОТЕХНИКА»
Методические указания
к лабораторным работам
по дисциплине «Математическое моделирование
и планирование эксперимента»
Ижевск 2002
УДК 621.31
Составитель: Артемьева Е. М., канд. техн. наук, доцент
Общая редакция: Барсуков В. К., канд. техн. наук, доцент
Рецензент - Юран С. И., канд. техн. наук, доцент ИжГСХА
Методические указания к лабораторным работам по дисциплине «Математическое моделирование и планирование эксперимента».– Ижевск: ИжГТУ, 2002 - 87 с.
Методические указания содержат описание шести лабораторных работ по дисцмплине «Математическое моделирование и планирование эксперимента» и предназначены для студентов специальности 181300 – «Электрооборудование и электрохозяйство предприятий, организаций и учреждений» высшего профессионального образования.
© Артемьева Е. М.
© Издательство ИжГТУ, 2002
Лабораторная работа №1
Исследование статистических характеристик случайных величин
Цель работы:
1. Ознакомление с методикой расчета оценок параметров распределения вероятностей случайной величины – математического ожидания и дисперсии.
2. Ознакомление с методикой проверки гипотезы о виде закона распределения вероятностей случайной величины.
Задание:
1. Определить статистические оценки математического ожидания и дисперсии исследуемой выборки случайной величины.
2. Проверить гипотезу о нормальном законе распределения вероятностей изучаемой случайной величины.
Вопросы для предварительной полготовки.
1. Нормальный закон распределения вероятности и его параметры. Кривая распределения плотности вероятности.
2. Распределение χ².
3. Распределение Стьюдента (t -распределение).
4. Распределение Фишера (F -распределение).
Основные теоретические положения
Статистическая оценка параметров
По выборке из генеральной совокупности получают выборочные статистические характеристики (выборочное среднее, выборочная дисперсия и т.п.), которые являются оценками соответствующих генеральных статистических характеристик.
Каждую выборочную характеристику также следует рассматривать как случайную величину, изменяющуюся от выборки к выборке.
Среди возможных оценок особую ценность представляют состоятельные и несмещенные оценки.
Оценка называется состоятельной, если с увеличением объема выборки она стремится (по вероятности) к оцениваемому параметру.
Оценка называется несмещенной, если ее математическое ожидание при любом объеме выборки равно оцениваемому параметру.
Состоятельными несмещенными оценками являются средние арифметическое наблюдаемых значений величины x:
 , (1)
, (1)
а также среднее квадратическое отклонение случайной величины x
 (2)
(2)
Величины  и S² являются оценками математического ожидания и дисперсии случайной величины x.
и S² являются оценками математического ожидания и дисперсии случайной величины x.
Расчет оценок по формулам (1), (2) становится громоздким с увеличением объема выборки. В этом случае целесообразно применять приближенную методику. Она состоит в том, что выборка преобразуется в формулу вариационного ряда:
- диапазон изменения случайной величины в выборке (xmin, xmax) делится на k интервалов, где число k находят по полуэмпирической формуле
k= 1+3,2 lg n, (3)
число k округляется до ближайшего целого. Длины интервалов обычно выбираются одинаковыми, равными
 ; (4)
; (4)
- затем определяется количество nm элементов выборки, попавших в каждый интервал [xm-1, xm] и рассчитывается относительная частота pm попадания случайной величины в соответствующий интервал
 ; (5)
; (5)
-вариационный ряд записывается в виде таблицы 1, причем элементам выборки, попавшим в m -ный интервал, приписывается значение xm*
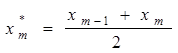 ; (6)
; (6)
ТАБЛИЦА 1
| M | (xm-1, xm) | X 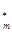
| nm | pm= 
|
| k | (xmin, x1) (x1, x2) (xk-1, xmax) | X  X
X  x
x 
| n1 n2 nk | p1 p2 pk |

| n |
- вариационный ряд может изображаться в виде графика (гистограммы).
Замечание: Предложенную процедуру построения вариационного ряда не следует считать единственно возможной. Количество интервалов, их длины могут варьироваться по усмотрению исследователя в зависимости от решаемой задачи.
По данным построенного вариационного ряда вычисляются оценки параметров распределения случайной величины x:
 ; (7) S 2=
; (7) S 2= 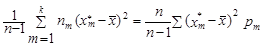 ². (8)
². (8)
Кроме того находятся доверительные интервалы математического ожидания mx и дисперсии σ  в предположении нормального закона расширения. Построение доверительного интервала для mx при неизвестной дисперсии σ
в предположении нормального закона расширения. Построение доверительного интервала для mx при неизвестной дисперсии σ  основано на том, что величина t
основано на том, что величина t
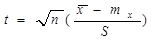 (9)
(9)
имеет распределение Стьюдента с v=n -1 степенями свободы.
Очевидно, что величина mx лежит в пределах интервала с границами 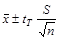 (рис.1):
(рис.1):
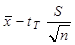 < mx <
< mx < 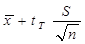 . (10)
. (10)
 |
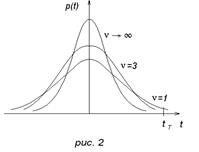
Величина tT находится по таблице t –распределения (распределения Стьюдента) (рис.2) случайной величины при вероятности надежной оценки p= 0,95и степени свободы v=n- 1.
Доверительный интервал для σ  строится на основании того, что величина
строится на основании того, что величина
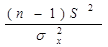 (11)
(11)
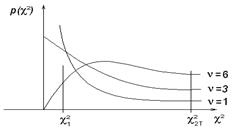
распределена по закону χ² (хи-квадрат) с ν=n- 1степеням свободы (рис.3). В этом случае находятся такие два числа χ 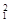 и χ
и χ  , что вероятности:
, что вероятности:
P { 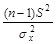 < χ
< χ 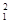 } =
} =  α (α= 0,05…0,1) (12)
α (α= 0,05…0,1) (12)
P {  > χ
> χ 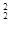 } =
} =  α. (13)
α. (13)
Следовательно,
P { χ 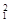 <
< 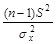 < χ
< χ  } = 1- α (14)
} = 1- α (14)
При этом доверительный интервал для σ  равен:
равен:
[ 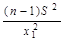 ,
,  ]. (15)
]. (15)
Значения χ 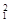 и χ
и χ  находят из таблицы χ² - распределение по известному числу степеней свободы ν=n- 1и вычисленным уровням значимости P1 и P2
находят из таблицы χ² - распределение по известному числу степеней свободы ν=n- 1и вычисленным уровням значимости P1 и P2
P1= { 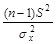 > χ
> χ 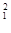 } = 1 -P {
} = 1 -P { 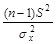 < χ
< χ 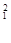 } = 1-
} = 1- 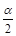 (16)
(16)
P2= {  > χ
> χ 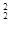 } =
} = 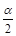 (17)
(17)
Статистическая проверка гипотез
Под статистическими гипотезами понимают некоторые предположения относительно значений генеральных статистических характеристик и генеральных распределений вероятности.
Проверка гипотезы заключается в сопоставлении некоторых статистических показателей (критериев проверки), вычисляемых по данным выборки, со значениями этих показателей, определенными теоретически в предположении, что проверяемая гипотеза верна.
Для критериев проверки выбираются определенные уровни значимости (α=0,1; 0,05; 0,02 и т.д.), отвечающие событиям, которые при проводимых исследованиях считаются (с некоторым риском) практически невозможными.
Следующим этапом является определение критической области применяемого критерия, вероятность попадания, в которую в случае, если гипотеза верна, в точности равна уровню значимости. Если α -уровень значимости, то вероятность попадания критерия в область допустимых значений равна 1 - α. Если значение критерия, вычисленное по данным выборки, окажется в критической области, то гипотеза бракуется.
При значениях критерия, принадлежащих области допустимых значений, можно лишь сделать заключение о том, что данные выборки не противоречат гипотезе.
Проверка гипотезы о равенстве математического ожидания заданному значению с.
Одна из наиболее часто встречающихся задач математической проверки гипотез заключается в сравнении центров распределения двух или более нормально распределенных величин X и Y или о равенстве математического ожидания какому-либо постоянному значению mx= c.
Такого рода предположения называют «нулевой» гипотезой (H0). При отсутствии конкурирующей гипотезы критической областью при проверке нулевой гипотезы является область больших по абсолютной величине значений. В качестве критерия проверки берётся величина
 , (18)
, (18)
называемая t – критерием. Величина t распределена по закону Стьюдента.
Если вычисленное значение t не превышает критического tT=tν,α,, найденного по таблице распределения Стьюдента при уровне значимости α и числу степеней свободы ν=n- 1, то исходная гипотеза не отвергается. [1, 2].
II –2. Проверка гипотезы о равенстве двух дисперсий
Пусть по данным двух выборок получены оценки дисперсий  и
и  со степенями свободы ν1=n1- 1 и ν2=n2 -1.
со степенями свободы ν1=n1- 1 и ν2=n2 -1.
Требуется выяснить, взяты ли данные выборки из генеральных совокупностей, имеющих одинаковые дисперсии
 =
=  . (19)
. (19)
Для проверки указанной гипотезы применяется F – критерий (дисперсионное отношение)
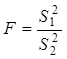 , (20)
, (20)
где 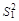 является бóльшей из двух оценок, т.е.
является бóльшей из двух оценок, т.е. 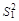 =max (
=max (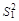 ,
, 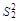 ). Величина F – отношения имеет F – распределения (распределение Фишера) со степенями свободы ν1=n1- 1 и ν2=n2 -1. (рис.4)ритическая область для F – критерия состоит из двух интервалов: больших значений, удовлетворяющих неравенству
). Величина F – отношения имеет F – распределения (распределение Фишера) со степенями свободы ν1=n1- 1 и ν2=n2 -1. (рис.4)ритическая область для F – критерия состоит из двух интервалов: больших значений, удовлетворяющих неравенству
F>F2 (21)
и интервала малых значений
 |
0<F<F1. (22)
критические точки подбираются так, что при уровне значимости q
P(F>F2)= 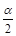 и P(F<F1)=
и P(F<F1)= 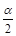 . (23)
. (23)
Поскольку левая критическая точка F – распределения соответствует правой критической точке  - распределения, то для определения F1 и F2 необходимо найти только правые точки для F и F’.
- распределения, то для определения F1 и F2 необходимо найти только правые точки для F и F’.
Ввиду указанного свойства табулированы только правые критические точки F – распределения для различных значений свободы ν1 и ν2 [1,2].
Принято отбрасывать гипотезу, когда величина F (F>1) превосходит верхнее критическое значение для уровня значимости 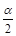 , а при этом вся критическая область будет отвечать уровню значимости α. Таким образом, если выполняется неравенство
, а при этом вся критическая область будет отвечать уровню значимости α. Таким образом, если выполняется неравенство
 |
то гипотеза о равенстве дисперсий
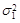 и
и  не принимается.
не принимается.
II-3. Проверка гипотезы относительно вида закона распределения вероятностей.
Для проверки гипотезы о том, что данная величина x подчинена закону распределения F(x), используются «критерии соответствия», основанные на выборе определенной меры расхождения между теоретическим (гипотетическим) и эмпирическим распределениями.
Если такая мера расхождения (т.е. критерий) для рассматриваемого случая превосходит установленный предел, то гипотеза не принимается.
Одним из наиболее распространенных критериев является критерий χ² (критерий Пирсона).
Пусть по данным выборки построена таблица 1, где nm количество попаданий случайной величины x в m -ный интервал.
Пусть 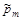 - вероятность попадания в m -ный интервал, вычисленная с использованием гипотетического распределения. Тогда критерий Пирсона запишется так:
- вероятность попадания в m -ный интервал, вычисленная с использованием гипотетического распределения. Тогда критерий Пирсона запишется так:
 (25)
(25)
здесь k– число интервалов, n –объем выборки. Величина χ² имеет ν=k-l- 1степеней свободы, где l – число оцениваемых параметров в законе распределения. Так, при нормальном распределении l= 2.
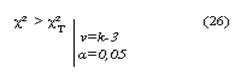 |
В случае
гипотеза о виде закона распределения не принимается
Порядок выполнения работы.
-Создать выборку значений случайной величины сопротивления нагрузки R энергосистемы, изменяющейся дискретно в пределах от Rmin до Rmax (принять, что Rmin=77 Ом, Rmax=95 Ом). Для этого следует использовать последовательность целых случайных чисел 0,1,… 9, полученную у преподавателя.
Числам 0,1,2,… 9 должны соответствовать определенные значения параметра R, находящиеся внутри диапазона от Rmin до Rmax. Для этого интервал значений R (рис..5) разбивают на 9 равных отрезков. Длина отрезка равна ∆:
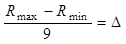
 |
В таблице 2 указаны значения RI в омах на концах отрезков, обозначенных числами 0, 1, 2,…9 (рис.5)
ТАБЛИЦА 2
| Ri (i =0…9) |
После этого составляют ряд случайных значений параметра R, параллельный заданному ряду случайных чисел от 0 до 9. Например, выборке чисел (0….9) 0, 9, 1, 1, 5, 1, 8, 6, 3, 5, 1, 2, 2, 5, 3… соответствует ряд значений параметра R (77…95) Ом: 77, 95, 79, 79, 87, 79, 93, 89, 83, 87, 79, 81, 81, 87, 83….
- Найти оценку математического ожидания  , оценку дисперсии S²{R} и проверить гипотезу о нормальном распределении вероятностей величины R. Для этого применить приближенную методику, которая состоит в следующем:
, оценку дисперсии S²{R} и проверить гипотезу о нормальном распределении вероятностей величины R. Для этого применить приближенную методику, которая состоит в следующем:
а) диапазон изменения случайной величины (Rmin, Rmax) делится на k интервалов, где k находится по формуле k= 1+3,2 lg n, где n - объем выборки. Полученное число k округляют до ближайшего целого; в нашем случае следует взять k =(5…7)<9;
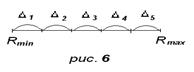
б) длины интервалов выбирают одинаковыми, равными
 (рис.6)
(рис.6)
 |
в) затем определяют количество nm значений R, попавших в каждый интервал, и относительную частоту

попадания величины R в соответствующий интервал.
 |
г) после этого выборочные данные записывают в виде таблицы 3 и гистограммы (рис.7)
ТАБЛИЦА 3
| m | (Rm-1, Rm) | 
| nm | 
|
д) оценки параметров распределения вычисляют по формулам (7), (8)
ж) затем проверяют гипотезу о нормальном распределении.
С этой целью находят величину χ²
 (25)
(25)
и сравнивают ее с табличным значением

[1,2].
В случае неравенства χ² < χ 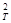 гипотеза о нормальном распределении не отвергается.
гипотеза о нормальном распределении не отвергается.
Результаты проверки гипотезы удобно представить в виде таблицы 4. В таблице 4 t – центрированная переменная, равная
 i= 1,2,…k
i= 1,2,…k
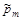 - вероятность попадания случайной величины t в m -ный интервал при гипотетическом распределении
- вероятность попадания случайной величины t в m -ный интервал при гипотетическом распределении
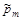 =P(tm)-P(tm-1)
=P(tm)-P(tm-1)
В случае проверки гипотезы о нормальном распределении значения функции P(tm) и P(tm-1) находят в таблице нормального распределения вероятностей [1,2].
ТАБЛИЦА 4
| m | nm | tm-1, tm | P(tm-1), P(tm) | 
| n 
| nm -n 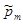
| (nm -n 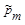 )² )²
| 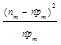
|
| 1 | n1 | -∞, 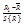
| 0, … | |||||
| 2 | n2 | 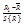 , , 
| …,… | |||||
| 3 | n3 |  , , 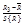
| …,… | |||||
| 4 | n4 |  , , 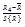
| …,… | |||||
| 5 | n5 | 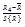 ,∞ ,∞
| …,1 | |||||

| 
|
1. Какова кривая плотности вероятностей нормального закона распределения? Какова кривая нормального распределения вероятностей?
2. Какие характеристики распределения вероятностей случайных величин Вы знаете?
3. Какими параметрами полностью определяется нормальное распределение и каковы их статистические оценки?
4. Как проверяется гипотеза о равенстве двух дисперсий?
5. Как проверяется гипотеза о виде закона распределения?
Литература
1. Ветцель Е.С. Теория вероятностей. – М.: Наука, 1964.
2. Гмурман В.С. Теория вероятностей и математическая статистика. – М.: В. ш., 1972.
3. Круг Г.К. Статистические методы в инженерных исследованиях: Лабораторный практикум. В.П. Бородюк и др. – М.: В. ш., 1983.
4. Смирнов Н.В., Дунин – Барковский И.В. Теория вероятностей и математическая статистика в технике. – М.: Физматгиз, 1965.
Приложение
Таблица случайных чисел от 0 до 9
Лабораторная работа №2






