Исходя из различных методов изображения, начертательная геометрия содержит 4 основных раздела, а именно: ортогональные проекции, проекции с числовыми отметками, аксонометрические проекции, перспективные проекции. Графические задачи, которые решаются одним методом, можно решать и любым другим. Но какой-то один будет наиболее удобен.
Все разделы начертательной геометрии пользуются одним методом – методом проецирования (от лат. projectio – бросать вперед, вдаль), поэтому чертежи, применяемые не только в начертательной геометрии, носят название проекционных чертежей. Изучение его начинают с построения проекции точки, так как при построении изображения любой пространственной формы объекта рассматривается ряд точек, принадлежащих этой форме. Метод проецирования заключается в том, что люба из множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность.
 |
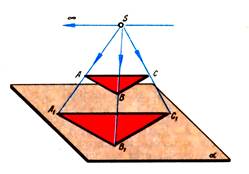
Центральные проекции. При центральном проецировании задают плоскость проекций Р и точку проекций S, не лежащую в плоскости проекций. Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пересечения этой прямой с плоскостью проекций и является центральной проекцией заданной точки на плоскость проекций Р. Прямые, проходящие через центр проекций и проецируемые точки, называют проецирующими прямыми.
 |
При центральном проецировании для однозначного определения положения точки в пространстве по ее проекции, нужны дополнительные условия, поэтому этот метод применяется редко.
Свойства центрального проецирования:
- При центральном проецировании:
а) точка проецируется в точку;
б) прямая, не проходящая через центр проекций, проецируется в прямую (проходящая – проецирующая прямая – в точку);
в) плоская двухмерная фигура, не принадлежащая проецирующей плоскости, проецируется в виде двухмерной фигуры (фигуры, принадлежащие проецирующей плоскости, проецируются вместе с ней в виде прямой);
г) трехмерная фигура отображается в виде двумерной.
- Центральные проекции фигур сохраняют взаимную принадлежность, непрерывность и некоторые другие геометрические свойства.
- При заданном центре проецирования проекции фигуры на // плоскостях подобны.
- Центральное проецирование устанавливает однозначное соответствие между фигурой и ее изображением, например изображения на киноэкране, фотопленке.
Параллельное проецирование – рассматривается как частный случай центрального проецирования, при котором центр проекций удален в бесконечность. При // проецировании применяют // проецирующие прямые, проведенные в заданном направлении относительно плоскости проекций. Если направление проецирования перпендикулярно плоскости проекций, то проекции называют прямоугольными или ортогональными, в остальных случаях – косоугольными.
 |
Свойства параллельного проецирования те же, что и при центральном, плюс еще одно свойство:
Параллельные проекции взаимно параллельных прямых параллельны, а отношение длин отрезков таких прямых равно отношению длин их проекций.
На ряду со свойствами параллельных проекций ортогональное проецирование имеет следующее свойство:
Ортогональные проекции 2-х взаимно перпендикулярных прямых, одна из которых // плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним, в первую очередь, относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях при определенных условиях формы и размеров проецируемой фигуры.
Эти преимущества обеспечили применение ортогонального проецирования для разработки чертежей во всех отраслях промышленности и строительстве.
Чертежи в проекциях с числовыми отметками построены в одной плоскости проекций называются однокартинными. Если информацию о расстоянии точки до картины дать с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют комплексным.






