Векторы и скаляры. Линейные действия над векторами.
Вектором а, называется множество всех направленных отрезков, имеющих одинаковую длину и направление. О всяком отрезке АВ из этого множества говорят, что он представляет вектор а. Длина отрезка АВ называется длиной (модулем) вектора а и обозначается символом |a|=|AB|. Модуль вектора – это скаляр.
Вектор нулевой длины, называется нулевым вектором и обозначается символом О. Векторы а и в, называются коллинеарными если они параллельны одной прямой. Векторы, параллельные одной плоскости, называются компланарными.
В b


a C
А
Два вектора называются равными, если они имеют одинаковый модуль, параллельны и направлены в одну и ту же сторону.
 |  |
a b
К линейным действиям над векторами относятся их сложение и умножение вектора на скаляр.
Пусть направленный отрезок АВ представляет вектор а. Приложив к точке В заданный вектор в, получим некоторый направленный отрезок ВС. Вектор, представляемый направленным отрезком АС, называется суммой векторов а и в и обозначается а + в. Суммой векторов а+в+с называется вектор R=OC, замыкающий ломаную ОАВС построенную
из данных векторов.
В частности, в параллелограмме, построенном на данных векторах ОА=а и ОВ = в, один вектор – диагональ ОС есть сумма а+в, а другой ВА есть разность а-в. Если дан вектор а=АВ, то вектор ВА называется противоположным вектором к вектору а и обозначается – а. Очевидно, что а+(-а)= 0. Вычесть какой - либо вектор – это значить прибавить противоположный. Отсюда следует, что в + (а - в)=в + [в + (-в)]=а+0=а.
Система векторов а ֽ ..., аn называется линейно-зависимой, если существуют числа λ1,..., λn такие, что хотя бы одна из них отлично от нуля и λ1 а 1 +...+ λn а n =0. В противном случае система называется ли  нейно – независимой.
нейно – независимой.
Проекция вектора.
Пусть вектор а составляет угол φ с осью Ох. Тогда проекция вектора на эту ось определяется формулой пре ≤ |а| · cosφ.
Проекция суммы векторов на ось равна сумме проекцией составляющих векторов на ту же ось:
Пре (а + в)=преа + прев.
Пусть даны точки А(x1,у1,z1) и В(х2,у2,z2). Проекция вектора а=АВ на оси координат: прx АВ=X=х2-х1
Прy АВ=Y=у2-у1 (1)
Прz АВ=Z=z2-z1
т.е а = {х2-х1; у2-у1; z2-z1}
Базис. Разложение вектора по базису.
Если е1, е2, е3 – базисы, то а = х1е1+х2е2+х3 е3 (2)
Числа х1, х2, х3 называются координатами вектора а в базисе β=(е1,е2,е3). Запись (2) называют также разложением вектора а по базису β.
Скалярным произведением двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла φ между ними: (
называется число, равное произведению длин этих векторов на косинус угла φ между ними: ( ) =
) = 
 = |
= |  |×|
|×|  |×cosφ
|×cosφ
Скалярное произведение обладает следующими основными свойствами:
- Скалярное произведение двух векторов не зависит от порядка этих сомножителей (переместительное свойство):

 =
= 

- Распределительное свойство. (
 +
+  )
)  =
=  +
+ 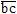 .
. - Скалярный квадрат вектора равен квадрату модуля этого вектора, т. е.
 2= |
2= |  |2
|2 - Скалярный множитель можно выносить за знак скалярного произведения, т. е. (λ
 ) = (
) = ( , λ
, λ 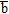 ) = λ(
) = λ( )
) - Скалярное произведение линейной комбинации векторов на произвольный вектор равно такой же линейной комбинации данных векторов на этот вектор, т. е. (λ
 + μ
+ μ 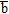 ,
,  ) = λ(
) = λ(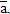 ,
,  ) + μ(
) + μ(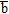 ,
,  )
)
Косинус угла φ= 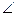 (
(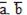 ) между двумя ненулевыми векторами
) между двумя ненулевыми векторами  и
и  равен cosφ=
равен cosφ=  .
.
Два вектора  и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 
Пусть  =ax
=ax  + ay
+ ay  + az
+ az 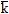 и
и  =bx
=bx  + by
+ by  + bz
+ bz 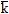 , тогда
, тогда 
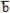 =axbx+ayby+azbz, здесь учтены, что
=axbx+ayby+azbz, здесь учтены, что 
 =
= 
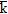 =
= 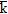
 = 0 и
= 0 и 
 =
= 
 =
= 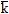
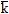 = 1
= 1
Поэтому косинус угла φ между двумя векторами  и
и  определяется cosφ= (axbx+ayby+azbz)/ (|
определяется cosφ= (axbx+ayby+azbz)/ (|  ||
||  |)
|)
Для перпендикулярных векторов  и
и  имеем φ=π/2 и, следовательно, cosφ=0, или axbx+ayby+azbz=0.
имеем φ=π/2 и, следовательно, cosφ=0, или axbx+ayby+azbz=0.
Под векторным произведением двух векторов  и
и  понимается вектор
понимается вектор  =
=  ×
×  =[a.b], для которого:
=[a.b], для которого:
1. Модуль равен площади параллелограмма, построенного на данных векторах, т.е. |c| = |a | |b|sinφ,где φ=∟(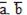 ), (0≤φ≤π) (рис 4.1);
), (0≤φ≤π) (рис 4.1);
 рис 4.1
рис 4.1
2. Этот вектор перпендикулярен перемножаемым векторам, т. е.  ┴
┴  и
и  ┴
┴ 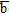 ;
;
3. Если векторы неколлинеарные, то векторы  ,
,  образуют правую тройку векторов.
образуют правую тройку векторов.
Основные свойства векторного произведения.
1. При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т. е.  ×
×  =-(
=-( ×
×  )
)
2. Векторный квадрат равен нуль-вектору, т. е.  ×
×  =0
=0
3. Скалярный множитель можно выносить за знак векторного произведения, т. е. если λ-скалярное, то (λ  ×
×  ) = (
) = ( ×λ
×λ  ) = λ(
) = λ( ×
×  )
)
4. Для любых трёх векторов a,b,c справедливо равенство ( +
+  )×
)× 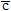 =(
=( )+(
)+(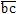 )
)
Необходимым и достаточным условием коллинеарности двух векторов  и
и  :
:  ×
×  =0
=0
Пусть  =ax
=ax  + ay
+ ay  + az
+ az 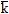 и
и  =bx
=bx  + by
+ by  + bz
+ bz 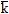 , тогда
, тогда
 ×
×  =
=  | ay az| -
| ay az| -  | ax az| +
| ax az| +  | ax ay|
| ax ay|
| by bz| |bx bz| | bx by |
Для удобства последняя формула записывается в виде определителя третьего порядка
| 

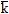 |
|
 ×
×  = | ax ay az|
= | ax ay az|
|bx by bz|
Под смешанным произведением  и
и  понимается число
понимается число 
Построим параллелепипед (рис 4.2), 
рис 4.2
Ребрами которого, исходящего из общей вершины О, являются векторы  и
и  . Тогда |
. Тогда |  ×
×  |=S представляет собой площадь параллелогромма, построенного на векторах
|=S представляет собой площадь параллелогромма, построенного на векторах  и
и  , т. е. площадь основания параллелипипеда. Высота этого параллелипипеда равна H= ±nр
, т. е. площадь основания параллелипипеда. Высота этого параллелипипеда равна H= ±nр 
 = ±|
= ±|  | cosφ, где
| cosφ, где  =
=  ×
×  и знак плюс соответствует острому углу φ=∟(
и знак плюс соответствует острому углу φ=∟(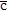 ,
,  ), а знак минус тупому углу φ. В первом случае векторы
), а знак минус тупому углу φ. В первом случае векторы  ,
,  образуют правую тройку, а во втором- левую тройку. Поэтому
образуют правую тройку, а во втором- левую тройку. Поэтому  =
=  = S np
= S np 
 =±V, т. е. объём параллелипипеда, построенного на векторах
=±V, т. е. объём параллелипипеда, построенного на векторах  ,
,  . Отсюда
. Отсюда  =±V.
=±V.
Основные свойства смешанного произведения
-
 =
= 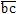
 =
= 

-


 =
= 
 =
= 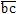
 =
= 

 =-
=- 
Необходимым и достаточным условием компланарности трёх векторов  ,
,  :
:  =0
=0
Если  = ax
= ax  + ay
+ ay  + az
+ az 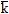 ,
,  =bx
=bx  + by
+ by  + bz
+ bz 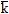 ,
,  =сx
=сx  + сy
+ сy  + сz
+ сz 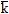 то
то
| ax + ay + az|
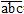 =| bx+ by + bz|
=| bx+ by + bz|
| сx + сy + сz|
Задание на СРС:
1. Вычисление длины вектора, угла между векторами. (Конспект. Срок сдачи по графику) [1,5,6]
2. Решить №1,3 из [2-стр. 273; 4], по вариантам.
Задание на СРСП:
1. Разложение вектора по базису. [3 – стр. 156 ]
Контрольные вопросы






