Активный раздаточный материал
Математика 1 ФОЕНП
Кредит 3 1-ый семестр
Лекция №14 «Интегрирование рациональных функций» 2013-2014 уч. год
Краткое содержание лекции
Интегрирование функций, содержащих квадратный трехчлен.
Здесь мы рассмотрим метод нахождения интегралов вида 
и 
.
. Выносим из квадратного трехчлена 
коэффициент 
и выделяем в нем полный квадрат.
Делаем в интеграле замену переменной 
, 
, в результате он приводится к виду 
или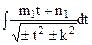 
.
Записываем интеграл в виде суммы двух интегралов в соответствии с двумя слагаемыми числителя. В первом интеграле делаем замену переменной 
. В результате оба слагаемых - табличные интегралы.
Интегрирование рациональных функций
Самый важный класс функций, интегралы от которых всегда выражаются через элементарные функции, представляют рациональные функции: 
, где 
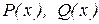- многочлены.
Если рациональная дробь неправильная, то с помощью деления 
на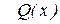 
можно выделить из нее целую часть и правильную рациональную дробь. Например:
Далее рассматриваем интегрирование только правильных рациональных дробей (т.е. дробей у которых степень многочлена в числителе ниже степени многочлена в знаменателе).
Рассмотрим вопрос о разложении рациональных дробей на простые дроби. Из алгебры известно, что всякий многочлен с вещественными коэффициентами степени выше второй разлагается единственным образом на линейные и квадратичные множители с вещественными коэффициентами.
Пусть многочлен 
разложен на множители в следующем виде:
Например. 1) 
2) 
3) 
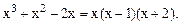
Интегрирование функций вида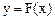 
, где 
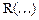- рациональная функция относительно аргументов
С помощью выделения полного квадрата в квадратном трехчлене и замены переменной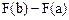 
интеграл 
приводится к одному из следующих трех видов (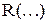
-рациональная функция);
. 
. Здесь с помощью замены переменной 
, 
= 
, 
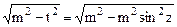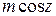этот интеграл преобразуется к виду 
.
. Интегралы вида 
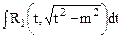находятся с помощью замены 
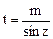, при этом 
, тогда 
.
. Интегралы вида 
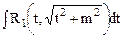находятся с помощью замены 
, при этом
.
Для специальных видов рациональной функции 
иногда проще использовать другие методы нахождения интегралов. Рассмотрим два из них.
. Интегралы вида 
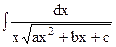находятся с помощью замены переменной 
, 
.
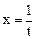. Интеграл 
, где 
- многочлен 
-ой степени можно записать в виде 
где 
- некоторый многочлен степени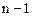 
, 
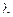-число. Коэффициенты и 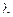находятся методом неопределенных коэффициентов после дифференцирования обеих частей записанного равенства.
Интегрирование некоторых тригонометрических функций
В этом пункте мы рассмотрим нахождение интегралов вида 
,
где 
- рациональная функция относительно 
.
Проверим, что такие интегралы с помощью универсальной замены переменной 
всегда сводятся к интегралам от рациональных функций. Так как 
, то 
.
В результате получаем, что 
.
Задание на СРС
1. Интегралы от функций, содержащих квадратный трехчлен.(конспект) [1,3,4].
2. Решение задач по теме [6; 2 - стр.340 № 1-6 ].(Срок сдачи -14 неделя)
Задание на СРСП
1. Смешанные задачи на интегрирование [2. ИДЗ-8.1,2]
Контрольные вопросы:
1. Интегрирование функций, содержащих квадратный трехчлен.
2. Интегрирование рациональных функций.
3. Интегрирование иррациональных функций.
4.Какая подстановка называется универсальной тригонометрической?
Глоссарий
| № | На русском языке | На казахском языке | На английском языке |
| Интегрирование Рациональная функция Иррациональная функция | Интегралдау Рационал функциясы Иррациоанал ф-сы |
Список литературы
Основная:
1. К.Кабдыкайыр. Сборник задач по Высшей математике. Учебное пособие. Алматы: «Дәуір», 2007. -408стр.
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов.- М.: Оникс, 2007, 2006
3. Байбазаров М.Б., Божанов Е.Т., Уразмагамбетова Э.У.Лекционный курс по математике. Учебное пособие, часть 1. Алматы, КазГАСА, 2003.
4. Индивидуальные задания по высшей математике под общей редакцией доктора физико-математических наук проф. А.П. Рябушко. Учебное пособие. II-часть.Минск, «Высшая школа», 2002г.
Дополнительная:
5. Сыдыкова Д.К. Математика 1. Методическое руководство к выполнению заданий для СРС. Алматы: КазГАСА, 2008.
6. Кремер Н.Ш., Путко Б.А. Высшая математика для экономистов. Учебник. Изд. Объединение «ЮНИТИ»,2006. - 479стр.
