Практическое занятие №4
Анализ рядов динамики
Учебный год
Задачи для аудиторной и самостоятельной работы
Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени.
Методика расчета среднего уровня в рядах динамики различна, обусловлена видом ряда динамики.
Задача 1
Имеются данные о продаже сахара в России.
| Годы | Продано сахара, тыс. тонн |
| Итого |
Рассчитайте среднегодовой объем реализации сахара населению России за 1994-1996 гг.
Методические указания
Средний уровень в интервальных рядах динамики исчисляется по формуле средней арифметической простой:

Y — уровни ряда (y1, y2,...,yn),
N — число периодов (число уровней ряда).
Задача 2
| 01.09.2003 | 01.09.2004 | 01.09.2005 | 01.09.2006 | 01.09.2007 | 01.09.2008 | |
| Численность студентов в высших учебных заведениях, тыс. чел. |
Рассчитайте среднюю численность студентов в высших учебных заведениях РФ за анализируемый период.
Методические указания
В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формуле средней хронологической:

y -уровни моментного ряда;
n -число моментов (уровней ряда);
n — 1 — число периодов времени (лет, кварталов, месяцев).
Задача 3
Списочная численность работников предприятия за октябрь такова: на 1 октября — 200 человек, 7 октября принято 15 человек, 12 октября уволен 1 человек, 21 октября принято 10 человек и до конца месяца приема и увольнения работников не было. Эту информацию можно представить в следующем виде:
| Число работников | Число дней (период времени) |
| 6 (с 1 по 6 включительно) | |
| 5 (с 7 по 11 включительно) | |
| 9 (с 12 по 20 включительно) | |
| 11 (с 21 по 31 включительно) |
Определить среднесписочную численность работников.
Методические указания
При определении среднего уровня ряда надо учесть продолжительность периодов между датами, т. е. применять формулу средней арифметической взвешенной:
Задача 4
Анализ динамики производства продукта "A" по предприятию за 1994-1998 гг.
| Годы | Произведено, тыс. т. | |
| 200,00 | ||
| 210,00 | ||
| 218,00 | ||
| 230,00 | ||
| 234,00 |
На основании данных таблицы:
1) Рассчитайте абсолютные приросты (цепные и базисные), коэффициенты роста (цепные и базисные), темпы роста (цепные и базисные). коэффициенты прироста (цепные и базисные), темпы прироста (цепные и базисные), коэффициенты опережения.
2) Рассчитай средний абсолютный прирост, средний коэффициент (темп) роста, средний коэффициент (темп) прироста, среднюю величину абсолютного значения 1% прироста за весь период наблюдения.
3) Изобразите ряд динамики графически.
Методические указания
Анализ рядов динамики
Для обоснованной оценки развития явлений во времени необходимо исчислить аналитические показатели: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста.
Абсолютные приросты (Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. — цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. — базисные абсолютные приросты). Формулы расчета можно записать следующим образом:

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 — цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 — базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:

Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 — цепные темпы роста) или по сравнению с начальным уровнем (гр.8 — базисные темпы роста). Формулы расчета можно записать следующим образом:

Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста). Формулы расчета можно записать следующим образом:
Тпр = Тр - 100% или Тпр= абсолютный прирост / уровень предшествующего периода * 100%
Абсолютное значение 1% прироста (гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. Определить величину абсолютного значения 1% прироста можно двумя способами:
уровень предшествующего периода разделить на 100;
цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.
Абсолютное значение 1% прироста = 
Средний годовой темп роста и средний годовой темп прироста
Среднегодовой темп роста исчисляется в следующей последовательности:
сначала по формуле средней геометрической исчисляют среднегодовой коэффициент роста (снижения) — 
на базе среднегодового коэффициента определяют среднегодовой темп роста ( ) путем умножения коэффициента на 100%:
) путем умножения коэффициента на 100%:

Среднегодовой темп прироста ( ) определяется путем вычитания из темпа роста 100%.
) определяется путем вычитания из темпа роста 100%.
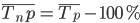
Среднегодовой коэффициент роста (снижения) по формулам средней геометрической может быть исчислен двумя способами:
1) на базе абсолютных показателей ряда динамики по формуле:

n — число уровней;
n — 1 — число лет в период;
2) на базе ежегодных коэффициентов роста по формуле

m — число коэффициентов.
Задача 5
Сезонные колебания потребления горючего в сельскохозяйственных предприятиях района за 3 года
| Месяцы | Расход горючего, тонн | Сумма за 3 года, т. | Ср. месячная за 3 года | Индекс сезонности в % | ||
| 1 год | 2 год | 3 год | ||||
| Январь | ||||||
| Февраль | ||||||
| Март | ||||||
| Апрель | ||||||
| Май | ||||||
| Июнь | ||||||
| Июль | ||||||
| Август | ||||||
| Сентябрь | ||||||
| Октябрь | ||||||
| Ноябрь | ||||||
| Декабрь | ||||||
| За год |
На основании данных таблицы:
1) РАССЧИТАЙТЕ индексы сезонности;
2) изобразите полученный ряд графически и охарактеризуйте общий вид динамики показателя;
Методические указания
Анализ сезонных колебаний
Задача статистики состоит в том, чтобы измерить сезонные различия в уровне показателей, а чтобы выявленные сезонные различия были закономерными (а не случайными) необходимо строить анализ на базе данных за несколько лет, по крайней мере не менее чем за три года. В табл. приведены исходные данные и методика анализа сезонных колебаний методом простой средней арифметической. Средняя величина за каждый месяц исчисляется по формуле средней арифметической простой.
Индекс сезонности (табл. гр.7.) исчисляется путем деления средних величин за каждый месяц на общую среднюю месячную величину, принятую за 100%. Средняя месячная за весь период может быть исчислена путем деления общего расхода горючего за три года на 36 месяцев или путем деления на 12 суммы средних месячных, т.е. суммарного итога по гр. 6: 12.
Для наглядности на основе индексов сезонности строится график сезонной волны. По оси абсцисс располагают месяцы, а по оси ординат — индексы сезонности в процентах (табл. гр.7). Общая средняя месячная за все годы располагается на уровне 100%, а средние месячные индексы сезонности в виде точек наносят на поле графика в соответствии с принятым масштабом по оси ординат.
Точки соединяют между собой плавной ломаной линией.
В табл. 11.7 (гр. 2) приведены фактические данные о производстве зерна в России за 1981- 1992 гг. (во всех категориях хозяйств, в весе после доработки)
Задача 6
В табл. приведены фактические данные о производстве зерна в России за 1981- 1992 гг. (во всех категориях хозяйств, в весе после доработки).
| Годы | Произв. млн. т. | Сред. за 3 года, млн.т. | Скользящая сумма за 5 лет, млн.т. | Расчетные показатели | |||||
| Сумма |    
| ||||||||
| 73,8 | |||||||||
| 104,3 | |||||||||
| 85,1 | |||||||||
| 98,6 | |||||||||
| 107,5 | |||||||||
| 98,6 | |||||||||
| 93,7 | |||||||||
| 104,8 | |||||||||
| 116,7 | |||||||||
| 89,1 | |||||||||
| 106,9 | |||||||||
| ИТОГО |
Произвести выравнивание данных:
1. Методом укрупнения интервалов (поквартальные данные, гр. 3);
2. Методом скользящей средней (гр. 4 и 5);
3. Методом аналитического выравнивания (гр. 6-9):
Методические указания
В приведенном примере должны быть исчислены пятизвенные (по пятилетним периодам) скользящие средние и отнесены к серединному году в соответствующем пятилетнем периоде. Так, за первые пять лет (1981-1985 гг.) по формуле средней арифметической простой исчислен среднегодовой объем производства зерна и записан в табл. против 1983 г.(73,8+ 98,0+ 104,3+ 85,1+ 98,6): 5= 92,0 млн. т; за второй пятилетний период (1982 — 1986 гг.) результат записан против 1984 г. (98,0 + 104,3 +85,1 + 98,6 + 107,5):5 =493,5:5 = 98,7 млн. т. За последующие пятилетние периоды расчет производится аналогичным способом путем исключения начального года и прибавления следующего за пятилетним периодом года и деления полученной суммы на пять. При этом методе концы ряда остаются пустыми.
Метод аналитического выравнивания (гр.6 — 9) основан на вычислении значений выравненного ряда по соответствующим математическим формулам. В табл. приведены вычисления по уравнению прямой линии:

Для определения параметров надо решить систему уравнений:







