Лк_6. Неинерциальные системы отсчета. Силы инерции.
Законы ньютоновской механики и соответствующие уравнения справедливы в инерциальных системах отсчета (ИСО). Очевидно, что в неинерциальных системах отсчета (НИСО), которые движутся с ускорением относительно ИСО, эти законы выполняться не будут. Однако путем введения в НИСО дополнительных сил, названных силами инерции, удается сохранить привычную форму уравнений движения, принятую в ИСО
Рассмотрим систему отсчета, движущуюся с постоянным ускорением а0 поступательно вдоль оси ОХ инерциальной системы отсчета (рис. 5.6). Для определенности координаты ИСО обозначим нештрихованными буквами, а координаты НИСО – штрихованными. Рассмотрим движение тела массой m под действием силы F в ИСО, т. е. в инерциальной системе отсчета. Основное уравнение динамики в этом случае запишется в обычном виде
Кинематическое соотношение радиус-векторов тела вытекает из рисунка
Дважды дифференцируя это равенство по времени, найдем связь между ускорением тела в инерциальной и неинерциальной системах отсчета.
После подстановки ускорения в уравнение движения получим:
Как и следовало ожидать, в НИСО уравнение движения изменилось. В НИСО произведение массы на ускорение тела не равно равнодействующей силе, действующей на тело со стороны других тел, и отличается от нее на величину, равную произведению массы тела на ускорение НИСО относительно ИСО, взятому со знаком минус. Если считать, что эта величина также является силой, вызванной ускоренным движением систем отсчета, то форма второго закона Ньютона сохранится и для описания движения тел в НИСО. Эту силу называют силой инерции Fи. С учетом сделанного замечания второй закон Ньютона для НИСО можно сформулировать следующим образом: произведение массы тела на ускорение равно сумме сил, определяемых взаимодействием тел, и сил инерции, действующих на тело в НИСО.
Введение сил инерции позволяет сохранить формализм второго закона Ньютона для описания движения тел в НИСО. Однако в НИСО не выполняются ни первый, ни третий законы Ньютона. Поэтому формулы, выведенные ранее с использованием этих законов в неинерциальных системах отсчета, будут не верны.
Равномерно вращающаяся система отсчета. Центробежная и Кориолиса силы инерции.
Такая НИСО часто встречается на практике. Суточное вращение земли означает, что мы живем во вращающейся системе отсчета. Если тело покоится в ней, то это означает, что сила инерции компенсирует силу, вызывающую центростремительное ускорение. Последняя равна F=-mω2R. Следовательно, сила инерции
Fи= mω2R (6.5).
Она направлена от центра вращения и называется центробежной силой инерции. Всем известно использование этой силы в центрифугах. Угловая скорость вращения земли невелика (7.3*10-5 1/с), поэтому центробежная сила инерции проявляется слабо.
Если же тело будет двигаться во вращающейся НИСО вдоль радиуса, то, в дополнение к центробежной, возникает еще одна сила инерции, названная силой Кориолиса. Действительно, если тело во вращающейся НИСО будет двигаться вдоль радиуса от оси вращения (рис. 5.3) по прямой A'-B', то за время dt его скорость в какой-либо инерциальной системе отсчета изменится как по величине - за счет того, что тело перейдет на другой радиус, так и по направлению, - за счет того что тело и направление движения повернутся на угол dφ. Причем оба приращения скорости совпадают по направлению и во вращающейся НИСО перпендикулярны направлению движения тела. Общее приращение скорости в ИСО будет равно
где u - скорость движения тела в НИСО. Общая величина Кориолисова ускорения будет равна
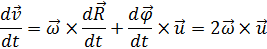
Соответствующая сила инерции Кориолиса
С точки зрения наблюдателя в ИСО тело будет двигаться ускоренно, так как на него действует сила, равная -mω2R, которая создает центростремительное ускорение, и сила, которая создает кориолисово ускорение. Эти силы вызываются взаимодействием движущегося тела со связью, обеспечивающей движение тела по определенной траектории. С точки зрения наблюдателя в НИСО движение тела равномерное, поэтому сумма сил, действующих на тело, включая центробежную силу инерции и силу Кориолиса, будет равна нулю. Траектория движения тела в НИСО - прямая линия.
Так как Земля вращается относительно оси, проходящей через ее центр, то система отсчета, связанная с Землей, является неинерциальной. Следовательно, в ней должно проявляться действие сил инерции. Действительно, существует ряд явлений, таких, например, как зависимость веса тела от широты места; отклонение тел, брошенных вертикально вниз, к востоку и к экватору; поворот плоскости колебаний маятника Фуко; размывание правого берега рек, текущих в северном полушарии в меридиональном направлении, которые можно объяснить действием сил инерции.
Механические колебания.
Колебательным называют движение, которое характеризуется определенной повторяемостью во времени. Колебания – распространенный в природе тип движения. Равномерное движение тела по окружности можно также считать колебанием. Удобным для изучения примером являются колебания маятников, с изучения которых начнем тему.
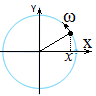
Для пояснения обозначений, применяемых при описании колебаний, рассмотрим равномерное движение материальной точки по окружности с угловой скоростью ω. В прямоугольной системе координат X-Y ее х-овая координата изменяется по закону
Используется следующая терминология:
Xm, наибольшее отклонение - амплитуда колебаний.
ωt+φ - фаза колебаний,
φ - начальная фаза колебаний,
ω- круговая частота,
Т – период – время совершения одного полного колебания 
,
- частота колебаний – количество колебаний в единицу времени. Между данными величинами выполняются соотношения:
ω=2πν, T=1/ν=2π/ω. (6.8)
Движение, при котором координата зависит от времени по закону синуса или косинуса (6.7), принято называть гармоническим колебанием.
Найдем зависимость от времени скорости (v=dx/dt) и ускорения
а=d2x/dt2) тела, смещение которого описывается формулой типа (6.7).
Как видно из (6.9), для гармонических колебаний между отклонением - x и ускорением a выполняется следующее соотношение:
Формула (6.10) является уравнением гармонических колебаний. Если какая-либо физическая величина, изменяясь во времени, подчиняется уравнению (6.10), то она зависит от времени по гармоническому закону:
