Пятиминутка: Закон движения точки задан уравнениями
x=2м/с*t; y=2м/с*t-1м/с2*t2
Найти координаты точки для моментов времени 0, 0.5с, 1с, 1.5с, 2с. Отметить положение точки в системе координат X-Y, провести траекторию, определить скорость точки (|v|) как функцию времени.
Из формулы (1.3) вытекает, что скорость любого движения можно представить как результат сложения скоростей трех прямолинейных движений вдоль координатных осей X,Y и Z,т.е. любое сложное движение можно представить как сумму прямолинейных движений (принцип суперпозиции движений). Используя данный принцип, определим, к примеру, величину первой космической скорости, т.е. такой скорости, параллельной земной поверхности, которую должно иметь тело, чтобы оно никогда не упало на Землю. Задача может быть решена следующим образом. Движение тела вдоль земной поверхности можно представить, как сумму двух движений: равномерного горизонтального движения со скоростью бросания v и свободного падения тела к поверхности Земли с ускорением g (ускорением свободного падения).
За малый промежуток времени Dt тело пройдет, двигаясь перпендикулярно земному радиусу, из точки А в точку В. (см.рис.1.9). При этом его радиус-вектор повернется на некоторый малый угол β. За это же за время, скорость тела получит приращение ∆v=g∆t вдоль земного радиуса, т.е. вектор скорости также повернется на некоторый угол. Для того, чтобы тело продолжало двигаться вдоль земной поверхности этот угол должен совпасть с углом поворота радиус-вектора тела. Следовательно, угол поворота вектора скорости - это также угол β. Приравняем тангенс β, найденный из треугольника перемещения и треугольника скорости:
(1.7)
После этого выразим величину скорости:
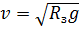. (1.8)
Как видно из вывода выражения для первой космической скорости, любое тело, двигаясь с этой скоростью вокруг Земли, изменяет направление скорости за счет постоянного падения на землю. и это изменение приводит к тому, что вектор скорости оказывается всегда параллелен земной поверхности.
Движение с неизменным вектором скорости называется равномерным. В общем случае скорость изменяется как по величине, так и по направлению.
Для характеристики быстроты изменения скорости вводится понятие ускорения. Ускорением называется отношение приращения скорости за бесконечно малый интервал времени к этому интервалу, т.е. производная от скорости по времени
(1.9)
Вектор ускорения можно также разложить по координатным осям:
(1.10)
Модуль вектора ускорения равен:
. (1.11)
Подставив в (1.9) выражение скорости как производную от радиус-вектора тела, получим выражение ускорения в виде второй производной от радиус-вектора по времени:
(1.12)
Пример. Радиус-вектор движущейся точки задан следующим выражением:
Определить характер движения, скорость и ускорение.
Для определения характера движения вычислим модуль радиус-вектора:
(1.13)
Таким образом, при движении точки |r|-const. Можно заключить, что это движение по окружности радиуса R с центром в начале координат.
Вычислим скорость движения точки:
(1.14)
Модуль скорости:
(1.15)
Модуль скорости также не изменяется во времени, следовательно, - это движение по окружности с постоянной по модулю скоростью.
Определим ускорение точки:
(1.16)
Сравнив формулы для радиус-вектора точки и ее ускорения, видим, что они выражают противоположно направленные векторы. Если радиус-вектор направлен из центра траектории к точке, то вектор ускорения направлен от точки в центр траектории. При этом модуль ускорения не изменяется во времени и равен |a|=Rω2. Вычислим скалярное произведение векторов скорости и ускорения:
Следовательно, в данном примере векторы скорости и ускорения перпендикулярны друг другу.
В общем случае векторы скорости и ускорения образуют какой-то угол. При этом удобно разложить вектор ускорения на две составляющие. Одна из них - 
параллельна (или антипараллельна) вектору скорости и называется тангенциальной составляющей ускорения. Другая - 
перпендикулярна вектору скорости, она называется нормальной составляющей ускорения. Тангенциальная составляющая ускорения выражает изменение модуля скорости, а нормальная составляющая - изменение направления скорости. В рассмотренном выше примере тангенциальная составляющего ускорения равна нулю. Вследствие этого скорость изменяется только по направлению, модуль ее остается неизменным.
В общем случае модуль полного ускорения определяется по теореме Пифагора:
1.3. Кинематика вращательного движения, вектор угловой скорости, связь линейно и угловой скорости точки, вектор углового ускорения.
Движение по окружности является частным, но весьма распространенным типом движения. Для него вводятся такие дополнительные кинематические характеристики как угловая скорость - ω и угловое ускорение - ε.
Величина угловой скорости w определяется как отношение приращения угла - dj, на который повернется радиус-вектор точки за время dt, к этому интервалу времени т.е.
(1.18)
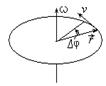
Это вполне естественное определение. Однако, согласно (1.18), и угол поворота и угловая скорость определились как векторные величины. В будущем мы увидим, что такое определение угловых величин оказывается очень удобным и продуктивным. Направление вектора угла поворота определяется правилом правого винта: если правый винт поворачивать в направлении положительного приращения угла, то поступательное движение винта укажет направление вектора приращения угла.
Похожее определение уже встречалось сегодня при определении векторного произведения. Действительно, если выразить приращение радиус-вектора точки, движущейся по окружности, при ее повороте на угол ∆φ, то получим следующую формулу
(1.19)
Вектор линейной скорости при движении точки по окружности с угловой скорость ω определится на основе (1.19)
(1.20)
Если начало координат совмещено с центром окружности как на рисунке 1.11, то радиус-вектор вращающейся точки и вектор угловой скорости взаимно перпендикулярны. при этом модуль их векторного произведения равен произведению модулей. Следовательно
Вектор углового ускорения 
определяется через изменение угловой скорости вращения за время Dt:
Вектор полного ускорения – это производная от скорости по времени. Из (1.20), получим
(1.22)
Первое слагаемое в (1.22) представляет собой вектор, перпендикулярный радиусу-вектору точки и лежит в плоскости вращения. Это означает, что он параллелен вектору скорости, т.е. - это тангенциальное ускорение точки. Второе слагаемое перпендикулярно вектору скорости. Следовательно - это нормальное ускорение.
Подставим вместо 
ее выражение (1.20) и распишем двойное векторное произведение. В результате получим:
Т.е. нормальное ускорение направлено против радиус-вектора - к центру вращения. Поэтому его называют центростремительным.
Пятиминутка. Материальная точка движется в пространственной системе координат XYZ по следующему закону изменения координат:
x=(2 м/c)*t; y=(10 м/с)*t-(5м/с2)*t2; z=(4 м/c)*t.
Определить координаты точки, ее скорость и ускорение в конце первой секунды движения.
