Компоненты перемещений и компоненты деформаций

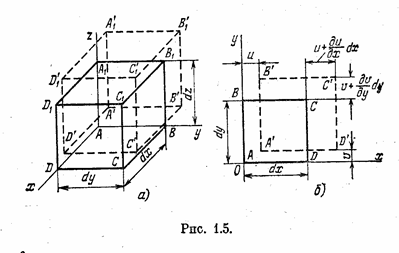
Для исследования деформаций вырежем из тела элемен­тарный параллелепипед ABCDA₁B₁C₁D₁, ребра которого рав­ны dx, dy, dz (рис. 1.5, а), и совместим начало координат с вершиной А. В результате деформации тела выделенный па­раллелепипед переместится в новое положение. При этом произойдет изменение длин ребер и искажение углов между Ребрами, прямых до деформации.

Новое положение параллелепипеда A'B'C'D'A’₁B’₁C’₁D’₁ без искажения углов между ребрами показано на рис. 1.5, а. Спроектируем первоначальное положение грани АВСD и новое положение этой грани А'В'CD' на координатную пло­скость хАу (рис. 1.5, б). При этом линейные перемещения точки А в направлении осей х и у обозначим соответствен­но через u и v. Линейное перемещение точки С в направлении оси х равно и + дu/дx dx, а в направлении оси у равно v + дv/дy dy. При этом ребро AD, которое до деформации имело длину dx, получит приращение длины, равное дu/дx dx, а реб­ро АВ, которое до деформации имело длину dy, получит приращение дv/дy dy.

 

Относительной линейной деформацией в точке по дан­ному направлению называется отношение изменения длины бесконечно малого линейного элемента к его первоначаль­ной длине.

Относительная линейная деформация ε_x в направлении оси х равна отношению приращения длины ребра дu/дx dxк его первоначальной длине dx, т. е.

 

 

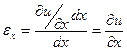
Аналогично получим ε_y = dv/dy. Рассматривая проекции других граней на координатные плоскости, таким же образом можно получить выражение для линейной деформации в направлении оси z, а именно ε_z = dw/dz, где w- линейное перемещение точки А в направлении оси z.

На рис. 1.6 показано искажение первоначально прямоугольной грани ABCD в результате угловой деформации. При этом точка D перемещается в точку D' и величина перемещения равна дv/дx dx, а точка В перемещается в В' ивеличина отрезка ВВ' равна дu/дy dy.

 

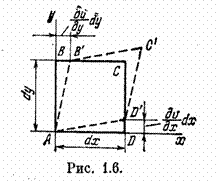
Угловой деформацией γ назы­вается величина искажения прямого угла, т.е γ = π/2 – B’AD’ = BAB’ + DAD’, где углы ВАВ' и DAD' измеряются в радианах. Так как эти углы очень малы, то их величину можно заменить тангенсами, т. е. принять

 

 

 

Таким образом, угловая деформация в плоскости хАу равна

 

 

Аналогично можно получить угловые деформации в плоско­сти xAz и yAz:

 

 

Запишем выражения для шести компонент относитель­ных линейных и угловых деформаций:

 

 

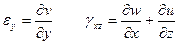(3.1)

 

 

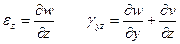
Дифференциальные зависимости (3.1) были получены Коши. Эти выражения для компонент деформации получены в предположении малости перемещений (линейных и угловых). Предполагается, что квадраты первых производных перемещений малы по сравнению с линейными и угловыми деформациями, а линейные и угловые деформации малы по сравнению с единицей.