ДОНЕЦЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА І-ІІІ СТУПЕНІВ № 89
ДОНЕЦЬКОЇ МІСЬКОЇ РАДИ ДОНЕЦЬКОЇ ОБЛАСТІ

(алгебра 8 клас)

Учитель: Петрікова Н.І.
(вища категорія,
старший вчитель)
М. ДОНЕЦЬК
ТЕМА «Квадратні корені».
Мета:
· Узагальнити і систематизувати знання, отримані учнями в процесі вивчення теми «Квадратні корені. Перетворення виразів з корінням».
· Вивчити і закріпити отримані вміння та навички.
· Розвивати вміння працювати в групі.
· Виховувати інтерес до знань, старанність, відповідальність перед
товаришами.
· Розвивати інформаційну компетентність, соціальну.
· Формувати поняття здорового способу життя і пропогандіровать його.
Очікувані результати.
Після уроку учні зможуть:
• застосовувати теоретичний матеріал про квадратні корені до вирішення вправ;
• навчитися усвідомленому застосуванню вивченого матеріалу під час
вирішення завдань;
• набути навичок роботи в малих групах;
• набути навичок логічних міркувань;
• формування мотивації здорового способу життя
Використані технології:
інтерактивні технології:
«Мікрофон»,
«Робота в малих групах».
Хід уроку

Зри в корень.
Кузьма Прутков.
I. Актуалізація навчальної діяльності.
Вступне слово вчителя.
Здравствуйте, ребята! Сьогодні ми з вами підведемо підсумок теми «Квадратні корені». (Повідомлення очікуваних результатів).Епіграфом нашого уроку є слова Кузьми Пруткова «Зри в корень», тобто дивися в суть чого-небудь. Поняття кореня і дії з ними є основою для багатьох тем у подальшому курсі математики. Тому мені б хотілося, щоб ви могли спиратися на знання з цієї теми у своїй роботі, як цей імпровізований чоловічок, символ нашого уроку.
Ви - здібні, талановиті й працелюбні, успіхів вам!
1.Для початку давайте повторимо теоретичну частину, але в наступній формі:
я починаю речення, а ви продовжуєте. Отже,
· Квадратним коренем з числа а називають... (число, квадрат якого дорівнює а).
· Арифметичним квадратним коренем з числа а називається... (невід'ємне число, квадрат якого дорівнює а).
· Дія, за допомогою якого обчислюють арифметичний квадратний корінь, називається... (здобування квадратного кореня).
· У записі √ а а називається... (подкореневим виразом).
· Запис √ а має зміст, якщо... (а ≥ о).
Давайте подивимося на таке завдання (малюнок 1):
Необхідно визначити, яке з чисел входить, а яке не входить в область визначення даного вирази: √ 1-х, х = 3; 0,9; 6; -1 4 / 5; 150.
Малюнок 1
При яких значеннях змінної вираз має зміст:

(Після рішення).
Хотілося б вам повідомити таку інформацію. У нашій країні:
• кожен 3 підліток курить;
• 6 кожен житель країни наркоман або пробував наркотик;
• на 150 жителів країни 1 людина інфікована СНІДом.
Дуже хотілося, щоб серед всіх цих категорій вас не виявилось, як і цих чисел немає в області визначення виразу.
2.Пригадали теорію, перейдемо до усного рахунку. Я називаю перше число, і необхідно знайти корінь з нього. Учень відповідає і передає «мікрофон» наступного, назвавши своє число і так далі. (Наприклад, √ 9 = 3,...)
3.Теперь спробуємо розгадати таке логічне завдання:
61/4 2/5
17/9? (3/4)
4. Нам потрібні сьогодні для роботи формули скороченого множення і властивості квадратного кореня. Уявімо себе в ролі «археологів» і відновимо втрачені записи.
1. √ (ав) =√ а √…, а≥0, в…
2. √(а/в) =√…/√…, а…, в…
3. (√а)2 = …, а…
4. √а2 = …, а…
5. √ а2к = а, а…
6. (а+в)2 = а2 +…+в2
7. (а-в)(а+в) = а2 - …
5.Спробуємо знайти відповіді на наступні завдання-загадки. Спочатку знайдемо принцип, за яким складено першу схема, а потім застосувати її до другої, щоб знайти відповідь на питання (малюнки 2 і 3)
Малюнок 2
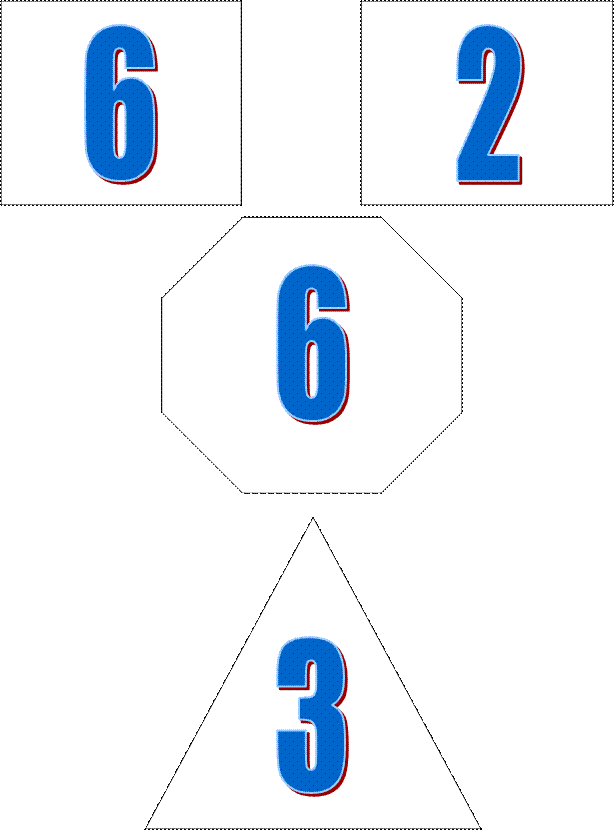
Малюнок 3

6.Теперь вам потрібно проявити увагу та все, що ми з вами повторили застосувати в такій ситуації. Необхідно перевірити виконані завдання деяким учнем і, якщо є помилки, виправить їх. Тобто спробувати себе в ролі «вчителя».
А) 7√ 2+5√ 2 = 12√4 = 12∙2=24
Б) 2√3=3√2, так як 2√3=√(2•3)=√6 и 3√2=√(2∙3)=√6.
В) (√ х-3)/(х-9)=(√ х-3)/((√ х)2-32)=1/(√ х+3).
Г) √ (-16а5 )=8а2 √ (–а).
II. Відпрацювання навичок. Інтерактивна частина.
Робота в малих групах».
Учні об'єднуються в групи по 4 особи (1 і 2, 3 і 4 парти), згадують правила роботи в групах, ділять обов'язки. Кожна група отримує завдання. Під час роботи на дошці записується умова завдань, вирішення яких групи запишуть після їх виконання (*-для 1-3 груп, **- для 4-6 груп). Коментуючи рішення з місця, разом аналізуємо допущені помилки.
Група № 1 (група № 4)
1.Упростіть вираз:
а)* (√ у-х)(√ у+х)-у=… б) (√ 5-2)2=… в)** 7 √2-3√ 2 +4 √18= …
Група №2 (група №5)
1 **. Позбутися від ірраціональності в знаменнику дробу 3 / (2 √ 6) =
2.Скоротіть дріб:
а) * (а-16) / (√ а-4) =... б) (15 - √ 15) / √ 15 =...
Група № 3 (група № 6)
1.** Порівняти 5 √ 3 і 3 √ 5.
2.Винести з-під знака кореня
а) √(6а2), а > 0; б)*√ (25х8у2), у < 0






