Однотипные силы тел, с которыми тела воздействуют друг на друга, направлены вдоль одной прямой, равны по модулю, но противоположны по направлению.

В виде формулы закон записывают так:

,

где F – силы одного и другого тела.

Центр масс (центр ине́рции, барице́нтр) в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Положение центра масс (центра инерции) в классической механике определяется следующим образом:

где

— радиус-вектор центра масс,

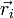— радиус-вектор i -й точки системы,

— масса i -й точки.

Для случая непрерывного распределения масс:

где:

— суммарная масса системы,

— объём,

— плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

11. Сила упругости — это сила, возникающая при упругой деформации тела и направленная в

сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:

1. действует между соседними слоями деформированного тела и приложена к каждому слою;

2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызываю-

щее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверх-

ностям (типичный пример — сила реакции опоры).

Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти

силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил

выходит далеко за рамки школьной программы.

В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и

сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей

данных тел.

Деформация называется малой, если изменение размеров тела много меньше его первона-

чальных размеров. При малых деформациях зависимость силы упругости от величины дефор-

мации оказывается линейной.

Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине дефор-

мации. В частности, для пружины, сжатой или растянутой на величину x, сила упругости

даётся формулой:

F = kx;

где k — коэффициент жёсткости пружины.

Коэффициент жёсткости зависит не только от материала пружины, но также от её формы

и размеров.

1При малых деформациях стержней имеется более детальная формула. Именно, если стер-

жень длиной l и площадью поперечного сечения S растянуть или сжать на величину x, то для

силы упругости справедлива формула:

F = ES

x

l

:

Здесь E — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометриче-

ских размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.

Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины

деформации справедлив лишь при малых деформациях тела. Когда деформации перестают

быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид.

 

12. Силы трения - появляются при перемещении соприкасающихся тел или их частей относительно друг друга.

Сухое трение - это трение между поверхностью двух тел при отсутствии смазки.

Вязкое трение (жидкое) - трение между жестким телом и жидкостью, а также между слоями жидкости или газа.

Сухое трение разделяется на:

1. Трение скольжения;

2. Трение качения.

Силы трения возникают не только при скольжении одной поверхности по другой, но также при попытке вызвать такое скольжение.

 

13. В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы m ₁ и m ₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

 

14. Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.

15. Понятие “работа“ как физическая величина во всех энциклопедиях, справочниках и учебниках раскрывается как понятие “ работа силы “ при описании прямолинейной механической формы движения. Правда, в физике применяется также и понятие “ работа поля “, которое трактуется, как “ работа сил поля “.

В БСЭ работа силы определяется, как “ мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения “. В метрологическом справочнике А.Чертова (1990) определение работы силы присутствует в виде словесной формулировки определяющего уравнения для элементарной работы силы F на элементарном перемещении d r без раскрытия ее физического содержания:

dA = F d r. (1)

Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

— средняя мощность

— мгновенная мощность

Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.

 

16. В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

§ — ротор консервативных сил равен 0;

§ — работа консервативных сил по произвольному замкнутому контуру равна 0;

§ — консервативная сила является градиентом некой скалярной функции U, называемой силовой. Эта функция равнапотенциальной энергии

взятой с обратным знаком.

 

ПОЛЯ ФИЗИЧЕСКИЕ, особая форма материи; физ. система, обладающая бесконечно большим числом степеней свободы. Примерами П. ф. могут служить электромагнитное и гравитационное поля, поле ядерных сил, а также волновые (квантованные) поля, соответствующие различным частицам.

 

17. Кинети́ческая эне́ргия — энергиямеханической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Единица измерения в системе СИ — Джоуль.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

– скалярная физическая величина, характеризующая движущееся тело и равная половине произведения массы частицы на квадрат ее скорости.

При скоростях, близких к скорости света, следует пользоваться релятивистским определением кинетической энергии, в соответствии с которым она равна разности между полной энергией частицы и ее энергией покоя.

Единицей кинетической энергии в СИ является джоуль (Дж).