Механика многофазных сред и математическое моделирование в трубопроводном транспорте

С.Н. Харламов, А.В. Рудаченко

 

 

Механика многофазных сред и математическое моделирование в трубопроводном транспорте

 

Учебное пособие

 

 

Издательство ТПУ

Томск 2005

ББК 24.7

УДК 665.6:622.621.64

Р 16

 

Харламов С.Н., Рудаченко А.В.

Р 16 Механика многофазных сред и математическое моделирование в трубопроводном транспорте: Учебное пособие. – Томск: Изд-во ТПУ, 2005. – 84 с.

 

В пособии представлены основные теоретические и экспериментальные результаты по проблемам математического моделирования многофазных сред в трубопроводном транспорте. Систематически излагаются механика и теплофизика сложных систем, особенности процессов переноса тепла, массы и импульса в гетерогенных средах. Представлены основы теорий гидродинамического, теплового и термодинамического подобия, схемы расчета структуры газожидкостных систем. Затронут широкий круг вопросов по теориям гидравлики и тепломассообмена трубопроводных систем, анизотропной турбулентности, как в однофазных, так и в двухфазных средах. Большое внимание уделяется анализу физического содержания процессов и методам описания межфазных взаимодействий, тепломассообмену в системах с флуктуациями.

Для студентов старших курсов, аспирантов вузов, научных работников и инженеров, занимающихся математическим моделированием и оптимизацией процессов в энергетике, химической технологии, нефтяной и газовой промышленности.

 

 

УДК 665.6:622.621.64

 

 

Рекомендовано к печати Редакционно-издательским советом Томского политехнического университета

 

Рецензенты

Доктор технических наук, профессор ТПУ

Н.А. Сваровская

 

Доктор физико-математических наук, главный технолог ОАО «Центрсибнефтепровод»

В.В. Жолобов

 

 

© Томский политехнический университет, 2005

© Оформление. Издательство ТПУ, 2005

 

ВВЕДЕНИЕ

 

Вследствие особого значения надежности трубопроводов для нефте- и газоснабжения велика роль методов математического моделирования течения сложных по структуре потоков. В условиях многообразия режимов работы сложных трубопроводных систем аналитические методы расчета весьма ограничены. Полное представление об особенностях процессов переноса в многокомпонентных гетерогенных или гомогенных смесях представляющих рабочее тело в трубопроводах, можно получить лишь на основе многопараметрических исследований всей картины теплогидродинамических параметров смеси. Широкое внедрение в практику управления процессами переноса вычислительной техники значительно расширило возможности исследований многофазных сред. Использование методов математического моделирования для расчета процессов в трубопроводах позволяет значительно сократить путь от принципиальной разработки процесса до его внедрения в практику. Математические модели всех процессов основаны на использовании тех или иных форм уравнений макроскопического переноса вещества и энергии и успех математического моделирования в большой мере определяется адекватностью и надежностью основных уравнений переноса. В силу этого в пособии уделяется большое внимание формулировке уравнений механики гетерогенных сред, методам описания физических явлений, сопровождающих течение и тепломассообмен в трубах, в широком диапазоне изменений определяющих параметров. Как известно, в отличие от уравнений механики гетерогенных сред, записанных феноменологически, уравнения, полученные пространственным осреднением, имеют то преимущество, что содержат в явном виде выражения для осредненных параметров фаз (в том числе таких величин как тензоры напряжений в фазах, интенсивности межфазного обмена массой, импульсом, моментом импульса, энергией) от функции локальных параметров фаз. В пособии уделяется внимание вопросам построения указанных выражений в виде зависимостей от средних макроскопических параметров. Такая задача весьма актуальна при моделировании гетерогенных сред на основе уравнений, полученных методом пространственного осреднения.

Цель пособия в анализе принципиальных вопросов математического моделирования процессов переноса в многофазных средах. На основе движений сложных систем исследуются процессы молекулярного и молярного переноса в условиях многообразия комбинаций фаз, их структуры, многообразия межфазных и внутрифазных взаимодействий и процессов (например, движений с существенной вязкостью фаз и межфазного трения; теплопроводности и межфазного теплообмена; фазовых переходов и химических реакций; дробления и коагуляции капель и пузырьков и т.д.). Центральными являются разделы, посвященные теории многоскоростного континуума, инженерным методам транспортировки рабочих смесей. Несмотря на краткость изложения, в пособии содержится ряд полезных сведений о методах моделирования сложных сдвиговых потоков. Сюда следует отнести методы интегральных преобразований и конформных отображений в задачах о медленных и умеренных движениях смесей, способы моделирования анизотропных турбулентных потоков. Полное и точное математическое описание всех этих процессов приводит к громоздким системам дифференциальных и интегро-дифференциальных уравнений, решение которых с необходимой точностью не всегда удается получить не только аналитически, но и даже численным методом. Поэтому в пособии уделяется также внимание методам теории подобия и анализа размерностей многофазных сред. Кроме того, в его центральных разделах представлены общие математические формулировки задач и отдельные результаты исследований, в частности, движений двухфазных смесей с тепломассообменом в трубопроводах. Такие данные представляют интерес при прогнозировании физических явлений, связанных с разделением фаз.

 

 

Раздел I. МНОГОФАЗНЫЕ СИСТЕМЫ

 

Глава I.1. Введение в механику и теорию процессов переноса

§ I.1.1. Механика многофазных сред – наука и инженерные приложения

В силу широкого распространения в природе и технике гетерогенных смесей с ними связывают перспективные технологические процессы производства и транспортировки сырья. Так, например, газо-парожидкостные среды, газовзвеси являются основным гидродинамическим объектом в энергетике, совместном транспорте нефти и газа, химической технологии, нефтепереработке и т.д.

Основные положения теории многофазных сред сформировались в механике сплошных сред (ММС) в 30х годах XX в. благодаря трудам советских, немецких и американских ученых: Д.Ф. Петерсона; Е. Шмидта; В.Беджера; М. Стыриковича; С.С. Кутателадзе и др. Именно термодинамика многофазных сред, как самостоятельный раздел ММС, позволяет анализировать сложные взаимодействия в средах при различных агрегатных состояниях вещества с наличием твердых частиц, жидких и газообразных компонентов смеси. Эти процессы осложнены физико-химическими превращениями и существенной переменностью физических свойств веществ. Законченные физико-математические постановки здесь часто отсутствуют, особенно это относится к проблемам турбулентности, процессам переноса в реагирующих средах. Более чем в других областях физики в механике многофазных сред, в силу сложности предмета, важными являются вопросы анализа подобия и моделирования, теории размерности, качественного исследования дифференциальных уравнений.

Предметом исследования в настоящей дисциплине являются каналовые течения смесей. Формы движения смесей в трубах разнообразны, например, в вертикальных участках каналов встречаются режимы: пузырьковый; снарядный; дисперсно-кольцевой; в горизонтальном канале – расслоенный; волновой; гребешковый; снарядный; пузырьковый; дисперсно-кольцевой; дисперсный. Заметим, что большинство таких режимов еще слабо изучены: существуют проблемы анализа устойчивости и многозначности представлений структуры течений. В этих вопросах важен выбор детальной математической модели.

Прикладные проблемы механики многофазных сред (ММФС) определяются развитием инженерного искусства в сторону использования более интенсивных энергетических процессов и широких интервалов изменения параметров состояния. В исследовании таких процессов опираются на статистическую физику, теорию молекулярного движения и межмолекулярного взаимодействия, физическую химию. Эти науки исходят из атомного и молекулярного строения вещества, при этом сначала выясняются свойства отдельных атомов и молекул, затем с помощью статистических методов выясняются глобальные свойства вещества. В этом заключается путь решения задач ММФС – от микроструктур к макроструктурам и макромасштабам. Стоит помнить, что движение от микроструктур к макроструктурам в построении общих законов и процессов переноса составляют основу статистического метода исследования явлений.

Замечание. Методы ММС уделяют особое внимание выяснению главных особенностей явлений переноса импульса, тепла и массы. Кроме того, уделяют внимание методам вычислений, дающим количественные результаты явления. Такие вычисления сложны и проводятся с помощью эффективных численных схем (будут рассмотрены в следующих частях пособия).

 

I.1.1.1. Проблемы моделирования МФС

С развитием вычислительной техники в большей степени завершенными выглядят такие разделы механики и теплофизики, как теплопроводность, ламинарная конвекция, радиация между твердыми телами, но до сих пор встречаются проблемы физико-математического содержания в области турбулентного теплообмена в МФС в каналах, гидродинамике в трубах, физико-химических процессах в несущей фазе и стенке. Это приводит к появлению большого количества эмпирических и полуэмпирических методов расчета процессов. Укажем основные проблемы, которые возникают при анализе процессов тепломассообмена (ТМО) и гидродинамики в трубах с МФСредами.

1. Движение высокотемпературных сред. В данных условиях возникают сложные структурные физико-химические процессы: плавления; конденсации и испарения; плавления и конвекции в жидком слое с последующим испарением; внутренней термодеструкцией при наличии гетерогенных и гомогенных химических реакций; поглощения тепла газами; излучения из объема материала; механического уноса в виде большого скопления мелкодисперсных частиц.

2. Описание турбулентного режима движения МФС. Здесь мелкодисперсные частицы потока частично увлекаются турбулентными пульсациями () и подавляют турбулентность (μ_t). Агломераты К-фазы из-за слабой чувствительности к пульсациям потока в поперечном движении вносят возмущения. Движение К-фазы поперек происходит под действием физических механизмов, которые требуют детального моделирования: молекулярной и молярной диффузии; турбулентной миграции; инерционного переноса; действия внешних массовых и центробежных сил; силы Саффмана, появляющейся в сдвиговом пристенном слое; силы Магнуса, возникающей при вращении частиц.

Замечание, связанное с трудностями моделирования и расчета молекулярной диффузии:

1. В неизотермических условиях многофазного течения молекулярная диффузия заметна лишь для очень мелких (субмикронных) частиц.

2. Турбулентная миграция и диффузия важна для мелких частиц.

3. Очень важно корректно рассчитывать инерционный механизм основных фракций К-фазы (он включает молекулярную диффузию вещества, ).

Замечание, связанное с решением задач о течении среы и осаждения полидисперсной К-фазы (агломерата материала стенки, частиц в потоке). Здесь возникают проблемы:

1. Физико-математического моделирования ТМП и трения в многокомпонентных химически реагирующих МФП потоках;

2. Моделирования ТМП в условиях возможного разрушения защитного материала стенки трубопровода;

3. Физико-математического моделирования теплового, химического и механического взаимодействия полидисперсных агломератов с К-фазой при движении среды.

Исследование данных проблем ТМП и гидрогазодинамики в МФС осуществляется методами физического и математического моделирования. Технологический цикл физического моделирования изучаемого явления включает: 1. Разработку методики эксперимента и установки опытного стенда. 2. Проведение тарировочных испытаний и испытаний средств регистрации параметрорв. 3. Проведение (в соответствии с выбранной стратегией) основных экспериментов. 4. Обработку и интерпретацию полученных результатов. 5. Построение физической модели.

Методы изучения физического моделирования ограничены трудностями переноса результатов модельных испытаний на натурные условия и невозможностью полного моделирования отдельных процессов, например, нестационарных с использованием критериев подобия. Это существенно ограничивает возможности методов физического моделирования. Здесь помогают методы математического моделирования и вычислительный эксперимент.

Определение математического моделирования (ММ). ММ (или вычислительный эксперимент) – это изучение физических явлений и процессов на основе математической модели с помощью ПЭВМ. Технологический цикл ММ состаит из: 1. Математической формулировки задачи в виде дифференциальных уравнений при соответствующих начальных и граничных условиях в рамках выбранной физической модели. 2. Разработки вычислительного алгоритма (дискретизации модели). 3. Реализации алгоритма в виде программы для ПЭВМ. 4. Обработки, анализа и интерпретации результатов численных расчетов. 5. Сопоставления расчетов с физическим экспериментом.

Замечание. Применение численных методов и ПЭВМ дает возможность использовать сложные нелинейные, многомерные, неизотермические модели, которые описывают существенные черты физических процессов. ММ дает определенные преимущества, но не позволяет полностью обойтись без опытной информации, поэтому приобретают актуальность вопросы эффективности численных методик.

 

I.1.1.2. Классификация задач процессов переноса в МФС

Задачи ТМО при течении МФС делятся на: прямые; обратные граничные; обратные коэффициентные; обратные ретроспективные. обратные геометрические.

Характеристика задач. Прямая – ее цель – в установлении причинно-следственных связей явлений и процессов ТМП. Обратная граничная и коэффициентная предназначены для получения граничных условий и коэффициентов дифференциальных уравнений процесса, например, теплофизических свойств, по известной ММ и опытным данным. Обратная ретроспективная – ее цель - в нахождении распределений температур, скоростей, уносов материала в предыдущие моменты времени. Обратная геометрическая – цель – в реконструировании законов перемещения потока, внутренней поверхности трубы или изотермы внутри стенки трубы.

 

§ I.1.2. Перспективы ММ гидрогазодинамики и ТПМ в МФСредах

Анализ современного состояния физико-математического моделирования сложных явлений в МФС позволяет заключить.

1. В настоящее время отсутствует детальная физико-математическая теория процессов переноса в МФС (как это имеет место для однофазных потоков) при тепловом, химическом и механическом воздействии фаз.

2. Существующие модели разрозненны и оценочны, т.к. содержат большое число допущений (например, приближения квазистационарного характера о нестационарных процессах течения и ТО; постоянство теплофизических свойств, замороженные химические реакции; допущения эмпирического характера). Все это не позволяет точно прогнозировать эффекты взаимовлияния (теплового, химического и механического характера) фаз на процессы переноса тепла и импульса.

3. Отсутствуют математические модели важных механизмов взаимодействия химии и турбулентности частиц несущей фазы.

4. Ограничены данные по анизотропному моделированию свойств турбулентного потока в МФС. Это требует привлечения к расчетам многопараметрических нелинейных моделей, учитывающих многомасштабность процессов.

 

§ I.1.3. Феноменологический и статистический методы изучения физических явлений

 

Все явления природы на основе представлений современной физики могут быть описаны двумя методами: феноменологическим и статистическим.

Определение. Метод описания процесса, игнорирующий микроскопическую структуру вещества и рассматривающий его как сплошную среду (континуум) называется феноменологическим ( ФМ).

Определимся в терминологии.

Определение. Среда, которую допустимо рассматривать как непрерывную (континуум), пренебрегая дискретным ее строением называется сплошной средой (СС).

Различают СС: однородная, неоднородная, изотропная, анизотропная, однофазная, многофазная.

Определение. Однородная СС – это СС, в разных точках которой ее физические свойства одинаковы при одинаковых температуре и давлении. Неоднородная СС – это СС, в разных точках которой ее физические свойства различны при одинаковых температуре и давлении. Изотропная СС - это СС, физические свойства которой не зависят от направления. Анизотропная СС - СС, физические свойства которой различны по разным направления. Однофазная СС – СС одно- или многокомпонентная среда, физические свойства которой в пространстве могут изменяться только непрерывно. Многофазная СС - СС одно- или многокомпонентная, состоящая из ряда однофазных частей, на границах которой ее физические свойства меняются скачком.

Т.к. в дальнейшем будем иметь дело с газообразными и жидкими средами, то приведем определения.

Определение. Жидкостью будем называть СС, обладающую свойством текучести, т.е. допускающую неограниченное изменение формы под действием сколь угодно малых сил.

Замечание. ФМ дает возможность установить некоторые общие соотношения между параметрами, характеризующими рассматриваемое явление в целом. Здесь законы носят общий характер, причем роль физической среды учитывается через коэффициенты (теплофизические свойства), полученные из опыта. С этой точки зрения законы Фурье, Ньютона, Фика и.д. – ФМ законы.

Определение. Статистический метод (СМ) – метод изучения физических явлений на основе исследования внутренней структуры вещества и обобщения их в макросвязи. Задача СМ – получение макроскопических характеристик по микроскопическим свойствам среды.

Замечание (д остоинства и недостатки ФМ и СМ).

1. Достоинство ФМ – в установлении общих связей между параметрами процесса с использованием эмпирической информации о процессе. Причем точность метода предопределена точностью данных из опыта. Недостаток ФМ – в наличии эмпирической информации.

2. Достоинство СМ – в получении искомых соотношений (законов) по заданным свойствам микроскопической структуры среды без дополнительного эксперимента. Здесь среда рассматривается как некоторая система, состоящая из огромного числа молекул, ионов, атомов с заданными свойствами. Недостаток СМ – сложность обобщения этих зависимостей и проблемы реализации метода, т.к. необходимо знать ряд параметров, которые могут быть определены в специальных разделах физики, химии, биологии и других областях знаний.

 

 

Раздел II. ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ МНОГОСКОРОСТНОГО КОНТИНУУМА

 

Глава II.1. Основные положения теории

§ II.1.1. Характеристика смесей

Гетерогенные неоднородные (или многофазные) смеси (сюда относятся газовзвеси, аэрозоли, суспензии, жидкости с пузырьками газа и т.д.) в отличие от гомогенных смесей (смесей газов, растворов, сплавов) характеризуются наличием макроскопических неоднородностей или включений по отношению к молекулярным масштабам. Кроме того, в гомогенных смесях составляющие смеси перемешаны на молекулярном уровне. Промежуточное положение между гетерогенными и гомогенными смесями занимают коллоидные смеси (коллоиды) и мицеллярные растворы.

Диспéрсные смеси. Это группа гетерогенных смесей (ГеС), которые состоят из двух фаз, одна из которых есть капли, пузырьки или твердые частицы. Различают следующие дисперсные смеси: суспензии – смеси жидкости с твердыми частицами; эмульсии – смеси жидкости с каплями другой жидкости; газовзвеси (аэровзвеси) – смеси газа с твердыми частицами или жидкими каплями – аэрозоли; пузырьковые среды – смеси жидкости с пузырьками газа или пара.

Иногда в специальной литературе по МСС суспензией называют любую дисперсную смесь. Дисперсную фазу составляют дисперсные частицы (капли, пузырьки, твердые частицы), а образует ее несущая фаза (жидкость, газ).

 

 

§ II.1.2. Главные допущения в математическом моделировании МФС

1. Размеры включений или неоднородностей в смеси (т.е. диаметры дисперсных частиц, капель, пузырьков в газовзвесях) представляются во много раз большими молекулярно-кинетических размеров в процессах (расстояний между молекулами, размеров кристаллической решетки, средних длин свободного пробега молекул) и также указанные неоднородности содержат большое количество молекул.

2. Размеры указанных неоднородностей во много раз меньше расстояний, на которых осредненные или макроскопические параметры смеси или фаз существенно меняются, а также, что размеры неоднородностей много меньше длин рассматриваемых в смесях волн, длин и параметров каналов, в которых течет МФС и т.д.

Замечание. Допущение 1 позволяет использовать классические представления и уравнения механики однофазных сред (уравнения идеальной и вязкой жидкостей, уравнения упругого и упруго-пластического тела и т.д.), для процессов внутри или около отдельных включений или неоднородностей (для смеси в целом – это микропроцессы). В рамках допущения 1 для описания физических свойств (μ,λ, E) можно использовать уравнения, параметры, полученные из опытов для веществ в однофазном состоянии.

Допущение 2 позволяет описывать макроскопические процессы в гетерогенной смеси (распространение в них волн, течений смесей в каналах, обтекание смесями тел и т.д.) методами МСС с помощью осредненных или макроскопических параметров.

 

 

§ II.1.3. Многоскоростной континуум

Описание методами МСС различного рода смесей (как ГоС, так и ГеС) связано с введением понятия многоскоростного континуума и определения взаимопроникающего движения составляющих.

Определение. Многоскоростной континуум представляет собой совокупность N континуумов, каждый из которых относится к своей составляющей (фазе или компоненте) смеси и заполняет один и тот же объем, занятый смесью. При этом, для каждого из этих составляющих континуумов в каждой точке пространства обычным образом определяется приведенная плотность ρ_i (масса i-той составляющей в единице объема среды), скорость (i=1 N), а затем и другие параметры, относящиеся к своему континууму и своей составляющей смеси.

Т. обр., в каждой точке объема, занятого смесью, будет определено N плотностей ρ_i, N скоростей и т.д. Параметры для смеси в целом имеют вид:

плотность смеси - ; среднемассовая скорость - (она же носит название барицентрическая скорость). Для удобства оценок эффектов переноса вводят диффузионные скорости - это скорости движения составляющих относительно центра масс смеси:

 

(1)

Для многоскоростной СС используют субстанциональные производные: (последняя – барицентрическая субстанциональная производная). Эти производные связаны с движением i- той составляющей и с движением среды в целом:

 

; (2)

 

. (3)

 

В (2), (3) имеется суммирование по повторяющемуся индексу (k). Роль дисперсных включений играет параметр i.

 

 

§ II.1.4. Модель взаимопроникающих континуумов

Известно, что математическое описание движения фаз МФС осуществляется при помощи осредненных величин физической системы. Поскольку в дисперсных МФС в сплошной фазе (жидкости или газе) всегда имеется значительное количество дисперсных включений (частиц, капель, пузырьков), то точное описание движения всех фаз такой системы на уровне отдельных дисперсных включений невозможно вследствие большого числа этих включений. Поэтому на практике имеют дело с некоторыми осредненными величинами фаз.

Такие сложные системы допускают представления механики взаимопроникающих взаимодействующих сплошных сред (континуумов) – модели взаимопроникающих континуумов (МВК). Применение МВК является правомерным, если для МФС существует физически бесконечномалый объем (ФБМО).

Определение ФБМО. Будем называть ФБМО такой объем среды, размеры которого пренебрежимо малы по сравнению с характерным пространственным масштабом макроскопического течения (т.е. масштабом, на котором осредненные параметры МФС меняются существенно).

Данное условие (условие 1) показывает, что осредненные по ФБМО характеристики МФС практически постоянны в пределах этого объема, при этом число дисперсных частиц в ФБМО должно быть настолько большим, чтобы осредненные по этому объему характеристики МФС были бы устойчивы по отношению к изменению объема.

Вывод 1. Для существования ФБМО необходимо, чтобы размер неоднородностей (в частности, дисперсных включений) в МФС был бы меньше расстояний, на которых макроскопические или осредненные параметры, характеризующие движение фаз МФС, существенно меняются.

Вывод 2. Введение ФБМО позволяет представить МФС как совокупность нескольких СС (по числу фаз), обладающих физическими свойствами фаз реальной МФС и непрерывно распределенных в пространстве, занимаемом МФС.

Другое условие (условие 2) существования МВК (считается выполненным).

Условие 2. Размер неоднородностей в МФС считается существенно превосходящим молекулярно-кинетические размеры (средние длины свободного пробега молекул, расстояния между молекулами и т.п., т.е. неоднородности содержат очень большое число молекул).

Вывод 3. Выполнение условия 2 позволяет использовать для описания движения отдельных дисперсных включений и окружающей их жидкости (газа) обычные уравнения и методы МСС.

 

 

Глава II.2. Элементы термодинамики многофазных структур

§ II.2.1. Газожидкостные и жидкостно-жидкостные системы

При совместном движении нескольких континуумов (газов, жидкостей, частиц) возникают взаимодействия на границах раздела фаз, которые ведут к образованию и эволюции динамических структур. Эти структуры и сами среды в движении следует описывать термодинамическими законами в рамках термодинамики, т.к. именно эта дисциплина занимается изучением макроскопических систем, пространственные размеры и время существования которых достаточны для проведения нормальных процессов измерения.

 

II.2.1.1. Методы исследования сложных динамических систем

Прежде чем рассматривать вопросы, связанные с описанием процессов переноса в физической системе, дадим определение самой физической системы.

Определение (с точки зрения термодинамики). Определить физическую систему (одно- и многофазную) это значит: выделить систему из окружающего мира и охарактеризовать состояние самой системы и внешние условия, в которых она находится.

Определение. Внешние условия для физической системы – набор параметров, определяющих положение внешних тел, взаимодействующих с системой.

Определяются внешние условия - обобщенными силами , где - набор параметров (i=1 m), обобщенные координаты силы А_i.

Состояние самой системы определяют внутренние параметры (ε, h, p, T).

Определение. Внутренние параметры для системы – параметры, зависящие от свойств самой системы и внешних параметров.

Первое начало термодинамики. Если в процессе взаимодействия системы с внешними телами меняется положение внешних тел, то система совершает работу. Общее выражение для работы, производимой системой

. (1)

Однако в процессе совершения работы физическая система меняет внутренние параметры. Система (однофазная, многофазная СС) может пребывать в разных термодинамических состояниях, она может быть изолированной (не взаимодействует с окружающей средой), замкнутой (не обменивается веществом с окружающей средой), открытой (обменивается теплом, массой с внешней средой). Тогда, если система адиабатически изолирована, то при изменении внешних параметров меняются ее внутренние параметры и из термодинамики имеем

-dE=dW, (2)

т.е. работа, совершаемая в этом случае системой или над системой, не зависит от пути перехода из одного равновесного состояния в другое (равновесное) состояние и равна изменению внутренней энергии. Тогда, например, в открытой системе имеем

dE=-dW+dQ+dZ. (3)

Из (3) следует, что изменение внутренней энергии (dE) идет за счет совершаемой работы (dW), за счет взаимодействия с окружающими средами, путем получения системой теплоты (dQ) от внешних тел и энергии переноса массы (dZ), (dZ= - термодинамический химический потонциал). По (3) видно, что можно рассчитать общее количество внутренней энергии, необходимое для перехода системы из одного равновесного состояния в другое, но нельзя определить какое время займет этот процесс. Равновесная термодинамика интересуется только начальным и конечным состоянием системы. Нам же важны процессы с их локальным характером изменения величин, особенности их изменений в пространстве и времени. Это отражают дифференциальные законы сохранения массы, импульса и энергии элемента объема СС.

Замечание. В неравновесной термодинамике ГеС рассматривается поведение каждой из фаз, взятых совместно с другими фазами, в отличие от равновесной, где фазы анализируются порознь.

 

II.2.1.2. Термодинамические параметры

Состояние ГеС и ГоС характеризуют термодинамические параметры, ответственные за превращение теплоты и работы – температура Т, давление р, объем V, массовая концентрация x. Состояние двухфазной системы определяется двумя независимыми параметрами: (p,x) или (T,x); (т.к. р и Т функционально связаны).

Согласно МВК для двухфазной среды имеем

1) объем смеси - , где - удельные объемы жидкости и пара, - массы жидкости и пара.

2) удельный объем среды (запись через x - степень сухости пара)

3) удельная внутренняя энергия u выражается через энергии составляющих фаз

4) удельная энтальпия

5) энтропия

В условиях испарения (конденсации) имеет место поглощение (выделение) теплоты, что характеризует λ – удельная теплота фазового перехода

- изотермический фазовый переход

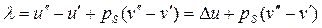- изобарический фазовый

переход.

Здесь p_S – давление насыщения, ∆u – внутренняя теплота фазового перехода, характеризует затраты энергии на изменение агрегатного состояния.

Для бесконечно малого процесса имеем

, (*)

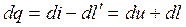где dq – количество полученной теплоты системой, . Тогда через параметры отдельных фаз уравнение (*) будет

(1)

Замечание. I начало термодинамики через теплоемкость двухфазной системы при неизменном значении концентрации (с_x) имеет вид

(2)

или через энтропию

или

(3)

 

§ II.2.2. Второе начало термодинамики

При бесконечно малом изменении состояния термодинамической системы изменение энтропии есть

(4)

 

Неравенство (4) характеризует направление протекающих макроскопических процессов.

Физический смысл II начала: устанавливает количественное соотношение между работой, которая может быть совершена физической системой при обратимом процессе и действительной работой. Действительная полезная внешняя работа меньше максимальной работы на величину . Поэтому произведение абсолютной температуры на приращение энтропии всей системы является потерей полезной работы из-за необратимости физического процесса

отсюда следует

(5)

Замечание. Из термодинамики имеем, внешняя полезная работа в обратимом процессе может быть выражена через разность термодинамических потенциалов.

Для двухфазной системы обратимый процесс может иметь место при p=const, T=const. Тогда из (5) следует

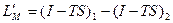
или, вводя изобарный потенциал Ф=I-TS, имеем .

Определение. Химическим термодинамическим потенциалом будем называть величину

(6)

Дифференциал химического потенциала есть

(7)

Тогда полный изобарный потенциал при (p,T)_const имеет вид

+…,

здесь m, φ_x – массы и химические потенциалы фаз, составляющие систему.

 

§ II.2.3. Частные случаи физической системы

Рассмотрим особые случаи системы – изменение агрегатного состояния, устойчивого и неустойчивого равновесия.

При смене агрегатного состояния (вещество переходит из одной фазы в другую) дифференциал изобарного потенциала имеет вид

(8)

Устойчивое равновесие системы характеризуется тем, что по устранению причины, вызывающей ее отклонение от равновесного состояния, система самопроизвольно возвращается в первоначальное равновесное состояние (принцип Ле-Шателье-Брауна). В изолированной системе (dq=0) термодинамическое равновесие характеризуется максимальным значением энтропии:

dS=0 и d²S≤0 (9)

Из (9) следует вывод: в данном случае никакие отклонения системы от равновесного состояния возникнуть самопроизвольно не могут, т.е. уменьшение энтропии в силу II начала термодинамики невозможно.

Неустойчивое равновесие. Характеризуется тем, что система будучи выведена из равновесия к исходному состоянию не возвращается, а переходит в другое устойчивое состояние.

Определение относительно устойчивых состояний. Метастабильные состояния (МС) – состояния равновесия систем, устойчивые по отношению к более удаленному состоянию. МС возможны в случаях, когда характеристические функции имеют несколько точек экстремума. При этом по истечении некоторого времени система из МС переходит в устойчивое (стабильное) состояние.

Замечание. Для двухфазной системы кроме механического и теплового равновесия (), () существующих фаз необходимо, чтобы устойчивости фаз в состоянии равновесия были одинаковыми. В этом случае термодинамический потенциал Ф двухфазной среды в состоянии равновесия должен иметь максимум, dФ=0. Тогда из (8) следует

.

Вывод: третье условие равновесия двухфазной системы - условие равенства химических потенциалов фаз –

(10)

При переходе к равновесному состоянию изобарный потенциал убывает (dФ<0), поэтому для двухфазной системы имеем: . Кроме того, учитывая, что при фазовом переходе выполняется , будет

. (11)

Замечание. Из (11) следует, что при , т.е. убывает масса первой фазы; при , т.е. убывает масса второй фазы.

Таким образом, из (11) имеем, что более устойчивой является фаза, имеющая меньший химический потенциал.

Для фазовых переходов I рода при пересечении кривой фазового равновесия скачком изменяются производные изотерм, изохор, изоэнтроп, изобар. Это связано с различием закономерностей в структуре вещества при изменении параметров состояния в однофазной и двухфазной областях.

Замечание (по математическому содержанию зависимостей для термодинамических функций МФС при наличии фазовых переходов). Переход системы через пограничные кривые не нарушает непрерывности изменения самих функций. Здесь терпят разрыв (в точках равновесных переходов) производные от термодинамических функций по термическим параметрам.

Пример. Рассмотрим скачок величины на пограничной кривой. Эта величина может быть полезна при характеристике скорости звука в МФС. Итак, полная производная от удельного объема (v) по давлению (p) вдоль линии насыщения (s) имеет вид

. (12)

Если в (12) производные взять один раз со стороны однофазной, а другой раз со стороны двухфазной области и приравнять правые части уравнений, то имеем

.

Учитывая, что и , следует, что

. (13)

Формулу (13) можно преобразовать, считая

; .

Тогда

. (14)

Здесь с_s – скорость звука, - теплоемкость при постоянном давлении на линии насыщения s.

Замечание. Одной из причин существования переходной зоны являются флуктуации параметров двухфазной среды, которые приводят к возникновению в устойчивой однофазной среде элементарных неустойчивых скоплений второй фазы. Причем интенсивность такого рода флуктуаций при подходе к пограничной кривой возрастает. (Указанный анализ опирается на данные связи теории устойчивости и флуктуаций).

 

Глава II.3. Элементы кинетической теории фазовых превращений

§ II.3.1. Гетерогенные флуктуации. Кинетическое уравнение

Активными механизмами образования фаз в потоке СС при ТО могут выступать испарение и конденсация.

Определение. Испарение (И) - парообразование с поверхности раздела жидкой, твердой и газообразной фаз, происходящее при произвольной температуре. Парообразование – переход вещества из жидкого или твердого состояния в газообразное (парообразное).

Определение. Конденсация (К) – переход вещества из газообразного состояния в жидкое или твердое. К в твердое состояние – десублимация. Различают К в объеме пара или парогазовой смеси и К на поверхности твердого тела или жидкости, с которыми пар (парогазовая смесь) находится в контакте.

Определение. Пленочная К - К в жидкое состояние на гидрофильной (хорошо смачиваемой жидкостью) поверхности твердого тела, при которой образуется сплошная пленка конденсата.

Определение. Капельная К - К в жидкое состояние на гидрофобной (несмачиваемой жидкостью) поверхности твердого тела, при которой на ней образуются отдельные капли конденсата.

Определение. Смешанная К - К в жидкое состояние на поверхности твердого тела, при которой на различных участках поверхности наблюдается как пленочная, так и капельная конденсация.

Определение. Контактная К - К пара непосредственно на поверхности жидкости (капель, струй и.т.д.).

Конденсация и испарение жидкости происходит в форме зародышей, которые можно рассматривать как маленькие капельки жидкости или пузырьки. Т.е. вновь возникшая фаза на начальном этапе процесса К (или И) является комплексом частиц, отличающихся малыми размерами от обычных макроскопических тел в агрегатном состоянии.

Для двухфазных систем (пар-жидкость) при радиусах капель r много больше толщины поверхностного слоя полный термодинамический потенциал есть

.

Здесь N₁, N₂ - числа частиц в фазах; - потенциалы, отнесенные к одной частице соответствующей фазы, при заданной температуре T и внешнем давлении p; σ – поверхностное натяжение капли. Индексы “1, 2” относятся к пару и жидкости соответственно.

Выше мы установили (из законов статистической физики), что система, испытывающая флуктуацию, может самопроизвольно перейти в менее вероятное состояние, характеризуемое уравнением энтропии. Однако, эти отклонения кратковременны, т.к. по прошествии времени релаксации система, находящаяся в неравновесном состоянии, переходит в более вероятное равновесное состояние.

 

§ II.3.2. Физический механизм перехода фаз

Здесь возможны случаи.

1. Если в термодинамически устойчивой системе с условием случайно (в порядке флуктуации) в старой устойчивой фазе возникло сгущение или разрежение, отвечающее появление новой фазы, то по прошествии короткого промежутка времени новообразования исчезли бы – флуктуация рассеилась.

2. В метастабильном состоянии (), когда устойчива новая фаза, малые флуктуации, соответствующие r<r_кр (r – радиус капли, r_кр – критический радиус капли, находящейся в состоянии термодинамического равновесия с окружающей средой) также неустойчивы, несмотря на то, что в макроскопических масштабах новая фаза является единственно устойчивой. При r>r_кр ситуация меняется. Флуктуации, превышающие r_кр, устойчивы и не распадаются. Дальнейший рост новой фазы происходит на таких устойчивых образованиях, т.к. любое дальнейшее увеличение их размеров способствует увеличению устойчивости флуктуации.

Замечание. Образование новой фазы не происходит внезапно во всем объеме старой фазы. Наоборот, образование сгустков молекул при конденсации и сгустков разрежения молекул при испарении носит характер локальных флуктуаций.

В отличие от обычных флуктуаций, совместимых с сохранением данного агрегатного состояния флуктуации плотности, выходящие за пределы одного, т.е. соответствующие образованию зародышей новой фазы (по Я.И. Френкелю) называются гетерофазными флуктуациями (ГфФ).

В отношении последних предполагается, что до начала обычного скачкообразного превращения исходная система не вполне гомогенна, а содержит зародыши новой фазы в форме пузырьков пара, капель жидкости, кристаллических зародышей и т.д.

 

II.3.2.1. Определение вероятности ГфФ

Согласно кинетической теории, мерой вероятности флуктуаций образования новой фазы в старой служит работа, которую должен был бы произвести внешний источник для ее образования, причем самораспределение числа капель представляется формулой Максвелла-Больциана (Гиббса)

 

(1)

Здесь С - постоянная (полное число молекул), N_g - число капель, содержащих g молекул жидкости в капле; ∆Ф - полное возрастание термодинамического потенциала (его преодоление ведет к образованию новой фазы):

 

(2)

g – размер молекул, - поверхность свободной энергии капли.

 

II.3.2.2. Образование зародышей новой фазы

На образование зародышей влияют неоднородности: капли, пылинки, кристаллы и др. частицы. При отсутствии посторонних ядер все центры конденсации образовываются из самих перенасыщенных паров благодаря местным флуктуациям параметров. Процессы самопроизвольного образования ядер центров конденсации описываются уравнением кинетики фазовых превращений Френкеля.

Для движущейся среды уравнение кинетики конденсации имеет вид:

 

(3)

 

Уравнение (3) – изменение числа капель, содержащих g молекул в единицу времени в единице объема при неравновесном распределении. Здесь - обусловлено соударенями молекул пара с каплями, содержащими g молекул и испарения молекулы пара с поверхности капель, содержащих (g+1) молекул; - неравновесное распределение капель; - скорость капель, состоящих из g молекул, I_g – увеличение числа капель, содержащих g молекул.

 

Глава II.4. Основные представления термогидродинамики МФС

§ II.4.1. Предпосылки моделирования МФС

Согласно модели МВК движение двух или нескольких сред следует рассматривать как движение их в пористой среде. Поэтому теоретическое решение о движении МФС связано с упрощением реальной картины, с идеализацией ее свойств и система ДУ МФС должна учитывать разрывность среды и происходящие в ней обменные процессы: массообмен, обмен энергией и количеством движения.

 

II.4.1.1. Схемы построения систем уравнений двухфазной среды

Схема 1. Включает уравнения: сохранения массы, количества движения энергии, состояния, теплообмена и кинетики фазовых переходов. Причем уравнения записываются отдельно для частиц паровой и жидкой фазы, находящихся в элементарном объеме даухфазной среды. Предполагается, что структура среды известна.

Недостатки подхода в решении задач. Значительные сложности формулировок, т.к. элементы дискретной фазы (капли, пузыри, частицы) в реальной среде очень разнообразны по форме и размерам и случайным образом распределены в пространстве.

Схема 2. Когда исходная разрывная среда с помощью того или иного метода интегрального преобразования превращается в фиктивную неразрывную среду.

Суть схемы. Предполагается, что каждая из фаз равномерно распределена в выделенном объеме и является сплошной. Фиктивная среда, как эквивалентная исходной, в то же время состоит из непрерывной жидкой и непрерывной паровой фаз, для которых уже можно применять аппарат дифференциального исчисления. Здесь, как и в схеме 1, паровая и жидкая фазы рассматриваются как раздельные системы, между которыми идут обменные процессы.

При создании модели гетерофазной среды используется осреднение параметров по некоторому интервалу времени и области пространства. Таким образом, формулировки законов переноса являются выражением общего пространственно-временного осреднения, зависящего от длины интервала или формы и объема области. Поэтому это приводит к множеству различных средних значений.

Схема 3. Учитываются положения: 1. Расположение фазы в пространстве. 2. Форма и размеры элементов дискретной фазы (капель, пузырьков, частиц), причем эти положения представляются случайными функциями. Вводится функция φ(x₁, x₂, x₃, τ), которая указывает вероятность того, что в окрестности данной точки пространства (x₁, x₂, x₃) в момент времени τ находится i-я фаза или же, что данная точка пространства (x₁, x₂, x₃) в момент τ принадлежит множеству точек i-й фазы. С другой стороны, вероятность φ(x₁, x₂, x₃, τ) может быть трактована, как объемная концентрация i-й фазы в данной точке пространства. Из построения ММ будет следовать однозначность модели. В схеме 3 применяется аппарат дифференциального и интегрального исчисления.

Замечание. Подразделение систем уравнений на фазы является условным приемом, т.к. решение системы уравнений невозможно без конкретизации структуры двухфазной среды.

Определение основных характеристик среды.

Выделим в схематизированной, гипотетической среде, эквивалентной исходной, произвольный объем V.

Определение. Объемной долей i-й фазы в данной точке а будем называть предел полученного количества φ_i при стягивании V в точку а:

(1)

По аналогии с (1) вводятся:

1. Характеристики концентраций отдельных фаз: а) истинная массовая степень сухости 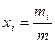- отношение истинной массы i-й фазы, находящейся в объеме V, ко всей массе среды в этом объеме. Иногда x_i называют “замороженной” степенью сухости; б) массовая расходная степень сухости - отношение расхода i-й фазы ко всему расходу среды в данном сечении потока; в) массовая равновесная диаграммная степень сухости – x_ig. Эта характеристика может быть получена из равновесных диаграмм или таблиц.

2. Здесь выполняются условия:

(2)

Для двухфазной среды имеют место связи

- истинная степень сухости; - расходная степень сухости, где ν=с₂/с₁ – отношение скоростей фаз или коэффициент скольжения.

 

II.4.1.2. Определение плотностей

Определение. Под местной плотностью МФС ρ будем понимать предел отношения массы вещества m, содержащегося в объеме V, к этому объему ρ =m/V. Истинная плотность i-й фазы ρ_i =m_i /V_i; парциальная плотность i-й фазы: ρ_iп =m_i /V. Здесь выполняются связи:

; . (3)

 

II.4.1.3. Скорости МФС

Определение. При местной плотности среды ρ средняя скорость МФС есть

. (4)

Истинная скорость движения отдельной фазы

, (5)

где S_i – часть площади S, занятая фазрй (S_i=φ_iS); G_i и G – расходы i-й фазы и среды в целом. Связь межлу средней скоростью среды и истинными скоростями отдельных фаз:

. (6)

Среднерасходная скорость . (7)

Из (6), (7), видно, что с_p записывается через сумму произведений истинных скоростей на расходные массовые концентрации фаз.

Среднеобъемная скорость . (8)

Среднеэнергетическая скорость . (9)

II.4.1.4. Классификация сил и их определения для МФС

Относительные массовые (или объемные) силы (напряжение или плотность силы), действующие на каждый элемент объема независимо от того, существуют или нет рядом с объемом другие части среды, определяются:

, (10)

где в - массовая сила, действующая на элементарную массу среды m, занимающую объем V.

Массовая сила, действующая на i-ю фазу

. (11)

Поскольку , то (12)

Определение. Напряжение поверхностных сил (НПС) (сил давления, трения) определяется как предел отношения поверхностной силы к площади при стягивании последней в точку; взаимосвязь П и П_i:

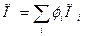. (13)

НПС на любой площадке складываются из нормальных p к выделенной площадке и касательных τ напряжений, определяемых вязкостью жидкости. Силы взаимодействия отдельных фаз внутри объема относятся к поверхностным и состоят из нормальных и касательных.

Замечание. Силы взаимодействия обусловлены скольжением отдельной фазы относительно других, однако, в целях упрощения записи уравнений количества движения и энергии принимают, что сила взаимодействия между фазами R является массовой (объемной).

Это допущение возможно при условии, что частицы малы и недеформируемы, т.е. что сила R действует на всю частицу независимо от истинного распределения нормальных и касательных напряжений.

 

§ II.4.2. Простейшие модели жидких сред

Основная система уравнений гидромеханики имеет вид

. (1)

Система (1) справедлива для любых жидкостей и газов, но в данном виде не несет информации о свойствах СС.

Свойства среды должны задаваться выражениями для тензора напряжений () и вектора теплового потока (). Рассмотрим наиболее употребительные модели тензора напряжений и вектора теплового потока. В выражения для и входят давление и температура, поэтому система (1) должна быть дополнена уравнением связи (ρ, T, p) ~ Ф(ρ, T, p)=0 – уравнением состояния.

 

II.4.2.1. Идеальная жидкость (ИЖ)

 

Определение. ИЖ – это жидкость, в которой напряжение, действующее на любую площадку с нормалью направлено перпендикулярно площадке. Иначе, в ИЖ имеются только нормальные напряжения и отсутствуют касательные.

Замечание. Реальные СС имеют касательные напряжения. Эти касательные напряжения равны нулю только в состоянии покоя или если СС движется как абсолютное твердое тело. Тогда РСС – идеальная, т.е. без трения.

 

II.4.2.2. Вязкая ньютоновская жидкость и тензор напряжения для нее

Налиие касательных напряжений и прилипания жидкости к стенке отличают РСС от идеальной среды. Сущность вязкости следует из зависимости

. (2)

Чтобы (2) выполнялось, к жидкости со стороны верхней пластины должна быть приложена касательная сила в направлении движения, уравновешивающая силы трения жидкости . Общее выражение:

. (3)

Здесь μ – динамическая вязкость. Закон (3) называется законом Ньютона. Реологическое уравнение (3) – частный случай общего закона, соответствующего любому пространственному движению вязкой жидкости – закон линейной связи между тензором напряжений и тензором скоростей деформаций - обобщенный закон Ньютона:

. (4)

Или в общей форме модель вязкой жидкости

. (5)

(5) – реологическое уравнение ньютоновской несжимаемой вязкой жидкости.

Определение. Вязкая среда несжимаема, если для нее div =0, ρ=const, тогда - скорость звука равна бесконечности (∞).

Определение. Вязкая теплопроводная сжимаемая СС - газ, если в ней возмущения распространяются с конечной скоростью распространения звука, , т.е. ρ=f(p,T).

Так, в изотермической среде

, . (6)

В адиабатической среде – пренебрегая отводом тепла при распространении звука –

. (7)

Когда газ – совершенный:

. (8)

Замечание. Скорость распространения звука в совершенном газе зависит лишь от абсолютной температуры и от физических свойств газа.

Газ – агрегатное существование вещества. Реальный газ (РГ) - это газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия. Для описания свойств РГ применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева ().

Общая запись модели РГ - , где - коэффициент сверхсжимаемости, функуция от .

Уравнение Ван-дер-Ваальса состояния РГ

 

, (9)

где - внутреннее давление, обусловленное силами притяжения молекул, b - поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами.

Уравнение состояния Бертло

. (10)

Здесь постоянные а, b связаны с пар