Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по формуле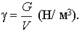 
Вязкость жидкости - свойство жидкости сопротивляться скольжению или сдвигу ее слоев.
динамическая вязкость равна 
где τ - касательные напряжения жидкости, τ = T/S. Вязкость жидкости зависит от температуры и от давления. При повышении температуры вязкость жидкости уменьшается и наоборот. У газов наблюдается обратное явление: с повышением температуры вязкость увеличивается, с понижением температуры - уменьшается.
Силы поверхностного натяжения - эти силы стремятся придать сферическую форму жидкости. Силы поверхностного натяжения обусловлены поверхностными силами и направлены всегда внутрь рассматриваемого объема перпендикулярно свободной поверхности жидкости. Рассмотрим бесконечно малый объем жидкости на свободной поверхности. На него будут действовать силы со стороны соседних объемов. В результате, если сложить вектора всех сил действующих на рассматриваемый объем, то суммарная составляющая сила будет направлена перпендикулярно внутрь рассматриваемого объема.
Температурное расширение - относительное изменение объема жидкости при увеличении температуры на 1°С при Р = const. Характеризуется коэффициентом температурного расширения 
Поскольку для капельных жидкостей коэффициент температурного расширения ничтожно мал, то при практических расчетах его не учитывают.
Испаряемость жидкости. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий в которых она находится: от температуры, от площади испарения, от давления, и от скорости движения газообразной среды над свободной поверхностью жидкости (от ветра).
Растворимость газов в жидкостях характеризуется объемом растворенного газа в единице объема жидкости и определяется по закону Генри: 
где VГ - объем растворенного газа; VЖ - объем жидкости; k - коэффициент растворимости; Р - давление; Ра - атмосферное давление.
Капиллярность - физическое явление, заключающееся в способности жидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах.
4. Гидростатическое давление (БЕЗ ДОКАЗАТЕЛЬСТВ) Гидростатическое давление - предел отношения нормальной сжимающей силы к элементарной площадке, на которой действует эта сила, при стремлении этой площадки к нулю: 
.Свойства гидростатического давления: 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. 2. Гидростатическое давление неизменно во всех направлениях. 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
5. Гидростатическое давление Атмосфе́рное давле́ние — гидростатическое давление воздуха, создаваемое притяжением атмосферы к Земле в поле тяжести на все находящиеся в ней предметы и земную поверхность. Избыточное давление – это давление сверх атмосферного, определенное без учёта атмосферного.может быть положительным и отрицательным. Абсолютным называется давление, определенное с учётом атмосферного давления.
6. Основное уравнение гидростатики 
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS - P0 dS - ρghdS = 0 Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем P = P0 + ρgh = P0 + hγ Полученное уравнение называют основным уравнением гидростатики. Закон Паскаля: давление на поверхность жидкости, производимое внешними силами, передаётся жидкостью одинаково во всех направлениях. Гидростатический парадокс — явление, при котором вес налитой в сосуд жидкости может отличаться от силы давления на дно. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Геронов фонтан Вот как это происходит. Вода из бутылки 1 по стеклянной трубке и шлангу сифоном течёт в бутылку 2 (до начала работы она была пуста) и вытесняет из нее воздух. Тот по шлангу поступает в бутыль 3 и буквально выдавливает из неё воду через опущенную почти до дна трубку. Проходя по шлангу, она бьет фонтаном. Теперь некоторые уточнения. Бутыль 1 должна располагаться выше, чем 2. Разность уровней воды в них обозначим через H. Бутыль 3 можно располагать, где угодно. Однако высота фонтана относительно уровня воды а этой бутыли не может быть больше H. Главное во всей конструкции - герметичность.
8. Уравнение Эйлера для равновесия жидкости Уравнение Эйлера для равновесия жидкости - совокупное дифференциальное уравнение равновесия жидкости под действием произвольных внешних сил.Если dP1 и dP2 - внешние силы, то условие равновесия: dP1 - dP2 + dFx = 0; где dFx = dM × ax, dM = r × dW, dW = dx × dy × dz.Сила гидростатического давления: dP = p × dw, если р1 и р2 - давление в точках приложения сил dР1 и dР2, то dР1 = p1 × dy × dz и dР2 = p2 × dy × dz. Если р = давление в центре тяжести, то: 
и 
. Уравнение равновесия: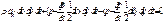 
, поскольку dy¹0 и dz¹0, то: 
. Аналогично для других координатных осей, получим уравнение Эйлера:
Сложив три уравнения получим: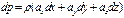 
, при постоянной плотности жидкости: 
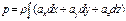. ГМТ постоянного давления называется поверхностью равного давления или поверхностью уровня.
9. Давление жидкости на плоскую стенку Пусть a - угол наклона стенки к горизонту, r - плотность жидкости, р0 - давление на свободной поверхности жидкости, h - расстояние от свободной поверхности жидкости до точки и l - расстояние до точки вдоль стенки, тогда: р = р0 + g × h = р0 + g × l × sin a; dP = p × dw = (р0 + g × l × sin a) dw, интегрируя по w получим: P = p0 × w + r × g sin a Sx, где Sx - статический момент относительно оси ^ стенке. Так как Sx = lцт × w, то P = (р0 + g × hц)w. 
точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.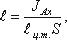 
где JАx - момент инерции площади S относительно центральной оси, параллельной Аx. В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.
10. Давление жидкости на криволинейную цилиндрическую поверхность Криволинейная цилиндрическая поверхность - образующая движется ïï себе самой вдоль криволинейной траектории. Внешнее давление не учитывается, так как компенсируется с обоих сторон поверхности. Действие окружающей жидкости заменяем силами G - вес рассматриваемого объема жидкости, Рх` - горизонтальная, Рz` - вертикальная и Рх, Рz - составляющие силы Р, действующей на криволинейную поверхность.Рх = Рх`, Pz = Pz` - G; P = Ö(Px2 + Pz2). Сила избыточного давления жидкости на криволинейную цилиндрическую поверхность равна геометрической сумме двух составляющих: горизонтальная численно равна силе давления жидкости на вертикальную проекцию криволинейной поверхности, а вертикальная - весу жидкости в объеме тела давления. Тело давления - объем жидкости, лежащий над криволинейной поверхностью, между вертикальными плоскостями, проходящими через крайние образующие и свободной поверхностью жидкости или ее продолжением. Px = g × hцт × wz; Pz = g × hцт × wх = g × Wтела давления, где wz и wх - площади вертикальной и горизонтальной проекций криволинейной поверхности.
11. Закон Архимеда, плавание тел Закон Архимеда: на погруженное в жидкость тело действует выталкивающая сила равная весу вытесненной жидкости.Плавает: Pz`` - Pz` > G; Равновесие: Pz`` - Pz` = G; Тонет: Pz`` - Pz` < G, где Pz`` = g × W(рассматриваемое тело + тело давления), а Pz` = g × W(тело давления). Значит: Pz`` - Pz` = g × W(рассматриваемое тело). Объемное водоизмещение - объем вытесненной жидкости. Центр водоизмещения - центр тяжести вытесненного объема жидкости.
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой (С – центр тяжести судна). Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.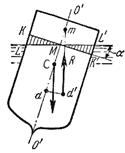 
Теперь рассмотрим условия равновесия судна: 1) если h > 0, то судно возвращается в первоначальное положение; 2) если h = 0, то это случай безразличного равновесия; 3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна. Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Ватерли́ния — линия соприкосновения спокойной поверхности воды с корпусом плавающего судна. Осадка - глубина погружения корабля или судна в воду. Запас плавучести - объем водонепроницаемого корпуса судна выше грузовой ватерлинии. Запас плавучести измеряется в процентах от водоизмещения корабля.
12. Основные виды движения жидкости: равномерное - движение жидкости, при котором величина скорости в любых живых сечениях потока одинакова. Неравномерное - при котором величина скорости изменяется в разл. живых сечениях потока. Установившееся - называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени. Неустановившееся - такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения. Напорное - движение, при к ром жидкость заполняет всё сечение закрытого русла (свободная поверхность отсутствует), а давление во всех точках потока выше атмосферного. Открытое (безнапорное) - огда движение жидкости происходит только под действием силы тяжести. Ламинарное и турбулентное. Линия тока - линия, касательная к каждой точке которой в данный момент времени совпадает с направлением вектора скорости. Поверхность тока — поверхность в поле течения, в каждой точке которой вектор скорости расположен в плоскости, касательной к этой поверхности в этой точке в данный момент времени. Трубка тока - трубка, составленная из линий тока, проходящих через точки небольшого замкнутого контура внутри движущейся жидкости. Элементарная струйка – это струйка, поперечные размеры которой настолько малы, что в каждом ее нормальном сечении параметры потока: V, p, r,..., – постоянны. Площадь живого сечения потока — площадь геометрической фигуры, образованной периметром водного потока при пересечении его вертикальной плоскостью. РАСХОД — жидкости (газа), количество жидкости (газа), протекающее в единицу времени через поперечное сечение потока.
13. Уравнение неразрывности движения для элементарной струйки и потока жидкости 1. Объемы жидкости, прошедшие через сечения в единицу времени, равны элементарным расходам: dQ1 = u1dw1 и dQ2 = u2dw2, так как объем струйки постоянный, то dQ1 = dQ2, а значит: u1dw1 = u2dw2 - уравнение неразрывности движения для элементарной струйки.
2. Для потока, как для совокупности элементарных струек: v1w1 = v2w2 - уравнение неразрывности движения для потока жидкости. Отношение средних скоростей в живых сечениях потока обратно пропорционально отношению их площадей.
3. Если ux - скорость в первом сечении, то 
- скорость во втором сечении. Масса жидкости, которая пройдет через первое сечение за время dt: r × ux × dy × dz × dt, через второе: 
Исходя из закона сохранение масс: 
, аналогично для движения по осям y и z, получим: 
- уравнение неразрывности движения для произвольного движения несжимаемой жидкости.
14. Уравнение Бернулли для элементарной струйки Так как: 
, то для идеальной жидкости, рассматривая два сечения получаем: 
.
15. Энергетический смысл: при u=0 - 
- основное уравнение гидростатики, так как 
- удельная энергия давления, а z - удельная энергия положения, то 
- удельная кинетическая энергия. 
. Геометрический смысл: - пьезометрический напор, z - напор положения, - скоростной напор.Для вязкой жидкости: 
, где hw1-2 - затраты на преодоление сопротивлений между 1 и 2 сечениями - потеря напора.
Полный запас удельной энергии потока (полный напор) определяется уравнением Бернулли и включает в себя:
высоту рассматриваемой точки над плоскостью отсчёта (высотный напор в поле тяготения),
давление жидкости, обусловленное упругим сжатием (гидростатический напор),
давление жидкости, обусловленное скоростью потока (скоростной напор).
Напорная линия графически изображает гидродинамические напоры вдоль потока. Отметки этой линии могут быть определены с помощью трубок Питó или же расчётом. По ходу движения она всегда падает, то есть имеет уклон, так как потери напора не обратимы. Пьезометрическая линия графически отражает напоры вдоль потока без скоростного напора hv=v2/2g, поэтому она располагается всегда ниже напорной линии. Отметки этой линии могут быть зарегистрированы непосредственно пьезометрами или, с пересчётом, манометрами. В отличие от напорной линии пьезометрическая может не только понижаться вдоль потока, но и повышаться.
16. Гидравлические элементы живого сечения: площадь живого сечения потока — площадь геометрической фигуры, образованной периметром водного потока при пересечении его вертикальной плоскостью. Смоченный периметр — длина части границы канала, касающейся жидкости. Гидравлический радиус R - отношение площади водного сечения потока F к смоченному периметру P. Режим движения, при котором отсутствуют пульсации скорости и перемешивание частиц, называется ламинарным. Режим движения, характерной особенностью которого является перемешивание частиц и пульсации скорости, называется турбулентным.
17. Критические скорости и числа Рейнольдса Верхняя критическая скорость - скорость при которой движение становится турбулентным. vвк = Reвк × d/n, где Reвк = 4000..20000 - верхнее критическое число Рейнольдса. Нижняя критическая скорость - скорость при которой движение становится ламинарным. vнк = Reнк × d/n, где Reнк = 2320 - нижнее критическое число Рейнольдса.Действительное число Рейнольдса: Re = vd/n, где n - кинематическая вязкость, зависящая от рода жидкости и ее температуры. При сравнении полученного Re с Reнк определяем режим движение жидкости.
18. Определение потерь напора по длине Ламинарный режим движения жидкости: так как средняя скорость в живом сечении потока: v = umax / 2, a umax = g × i × r2 / 4m, где umax - максимальная скорость, g - удельный вес жидкости, i - гидравлический уклон, r - геометрический радиус трубы, m - динамическая вязкость, то i = 8mv / gr2. Поскольку g = rg, Re = vd/n и m/r = n, то i = 32nv/gr2 = 64v2/2gRed - потеря напора при ламинарном режиме пропорциональна средней скорости, зависит от рода жидкости и обратно пропорциональна диаметру трубы. Итак - l = 64 / Re и 
.
19. Формула Дарси — Вейсбаха 
где
Δh — потери напора на гидравлическом сопротивлении;
ξ — коэффициент потерь (коэффициент Дарси);
V — средняя скорость течения жидкости;
g — ускорение свободного падения;
величина 
называется скоростным (или динамическим) напором.
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где
ΔP — потери давления на гидравлическом сопротивлении;
ρ — плотность жидкости.
Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D, то коэффициент Дарси определяется следующим образом: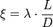 
где λ — коэффициент потерь на трение по длине. Следовательно ф-ла В.—Д. 
24. Турбулентный режим движения жидкости: , l - определяется только по эмпирическим формулам: область гидравлически гладких труб - l = 0.3164 / Re0.25, где 3000<Re<20d/D; переходная область - l = 0.11(D/d + 68/Re)0.25; где 20d/D<Re<500d/D; область гидравлически шероховатых труб - l = 0.11(D/d)0.25; где Re>500d/D
28. 29. К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы. 1. При внезапном расширении трубы: 
где S1 и S2 — площади поперечного сечения трубы, соответственно перед расширением и после него. И подставляем в формулу для потерь напора 
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле: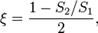 
где S1 и S2 — площади поперечного сечения трубы, соответственно, перед сужением и после него.
При постепенном сужении трубы (конфузор):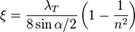 
где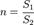 
— степень сужения; λT — коэффициент потерь на трение по длине при турбулентном режиме.
При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям.При повороте на 90 к-т Дарси опредся по формуле: 
где коэффициент сопротивления отвода 
30. Кавитация — нарушение сплошности (однородности) потока жидкости вследствие образования в нем «пустот» — мелких пузырьков и целых полостей, заполненных парами, воздухом и др. газами, выделившимися из жидкости. Кавитация возникает при понижении давления в жидкости ниже атмосферного до давления насыщения паров. Явление кавитации совершенно одинаково и для потока, обтекающего неподвижное тело, и для среды, в которой движется тело. В обоих случаях важны лишь относительная скорость и абсолютное давление. Соотношение между давлением и скоростью, при которых происходит кавитация, дается безразмерным критерием s, который называется кавитационным коэффициентом (числом кавитации) и определяется выражением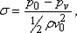 
где pv – давление насыщенного пара жидкости при данной температуре.
31. У равнения Бернулли для потока жидкости Энергетический смысл: 
- полная удельная энергия потока в живом сечении, так как - потенциальная удельная энергия давления, а z - потенциальная удельная энергия положения, то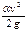 
- удельная кинетическая энергия, где v - средняя скорость в сечении; hw1-2 - затраты энергии на преодоление сил сопротивления. Геометрический смысл: - полный напор, так как - пьезометрический напор, а z - напор положения, то 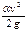- скоростной напор; hw1-2 - потерянный напор. Пьезометрическая линия - ГМТ концов отрезков суммы 
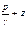. Пьезометрический уклон - изменение пьезометрической линии на единицу длинны. Напорная линия - ГМТ концов отрезков суммы . Гидравлический уклон - изменение напорной линии на единицу длинны.
32. Уравнение движения несжимаемой идеальной жидкости с условием ρ = const:
ρvi,0 + (p + ½ρv2),i = Fi. Здесь p – давление жидкости.
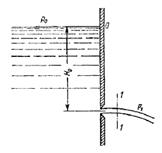33. Истечение через малые отверстия в тонкой стенке при постоянном напоре Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности. Скорость истечения жидкости через отверстие такое отверстие 
где Н - напор жидкости, определяется как 
φ- коэффициент скорости 
где α - коэффициент Кориолиса; ζ- коэффициент сопротивления отверстия.
Степень сжатия оценивается коэффициентом сжатия.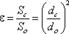 
где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dс и dо - диаметры струи и отверстия соответственно. Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.
, где. 
Эта формула называется формулой Торричелли и определяет скорость истечения жидкости из отверстия. Она получена для идеальной жидкости.Из формулы Торричелли следует, что скорость истечения жидкости из отверстия одинакова для всех жидкостей и зависит лишь от высоты, с которой жидкость опустилась. Она оказывается равной скорости свободного падения тела с той же высоты. Для реальных жидкостей скорость будет меньше, она зависит от формы, размера отверстия и от вязкости жидкости.
34. Истечение под уровень Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью. такой случай называется истечением под уровень, или истечением через затопленное отверстие.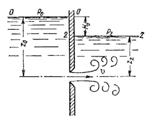 
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении. Скорость истечения в сжатом сечении струи 
где φ - коэффициент скорости; Н - расчетный напор, 
. Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
35. Время опорожнения сосуда. Для время полного опорожнения 
, где Н – высота сосуда, h – переменная высота уровня жидкости в сосуде, S – площадь сечения резервуара(постоянная для данного случая), S0 – площадь отверстия.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) выразим зависимость переменной площади S от h: 
где l - длина цистерны; D - диаметр цистерны. Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным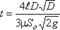 
37. 38. Насадки, скорость и расход при истечении жидкости через насадки при постоянном напоре Насадки - присоединенные к отверстию патрубки длиной l<4d, позволяющие существенно изменять скорость и напор. Бывают:внешние и внутренние;призматические, цилиндрические, конические (сходящиеся и расходящиеся) и коноидальные. Скорость и расход при истечении: 
, где 0-0 сечение - свободная поверхность жидкости, а 1-1 - сечение вблизи насадки. p0 = p1 = pатм, z0 - z1 = H. 
, где zм - коэффициент местных потерь.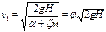 
, где j - коэффициент скорости. Расход: Q = w1 × v1 = e × wнасадки × v1, где e - коэффициент сжатия струи. 
, где m - коэффициент расхода жидкости.Для внешней цилиндрической насадки:
| j | e | m |
| 0.82 | 1.00 | 0.82 |
Классификация насадок:
1. цилиндрические - на входе в насадку обрасуется вакуум, который подсасывает жидкость и увеличивает расход. Срыв вакуума происходит когда напор превышает атмосферное давление;
2. конические сходящиеся - уменьшение расхода, увеличение скорости;
3. конические расходящиеся - уменьшение скорости, увеличение расхода. Угол конусности ограничен, иначе истечение происходит как из отверстия в тонкой стенке;
4. коноидальные - увеличение расхода, увеличение скорости.
39. 40. Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Повышение давления при гидравлическом ударе можно определить по формуле ΔPуд = ρυ0c
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
где r - радиус трубопровода;
E - модуль упругости материала трубы;
δ - толщина стенки трубопровода;
K - объемный модуль упругости
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E =, то скорость ударной волны определится из выражения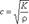 
Фазы гидроудара: заполнение трубы,встреча с препятствием, рост зоны повышенного давления, максимум повышенного давления, начало обратного движения, окончание сжатия, фаза разрежения.
41. Прямой и непрямой удары. Прямой удар происходит при времени закрытия задвижки
t3 < 2L/C где L - расстояние до резервуара способного поддерживать постоянное давление.
C - скорость распространения ударной волны.
Непрямой гидравлический удар при t3 > 2L/C. Такой удар характеризуется меньшей силой, чем прямой удар.
42. Гидротаранный насос или гидравлический таран — механическое устройство для подъёма воды на значительную (до нескольких десятков метров) высоту. Не требует для работы каких-либо внешних движителей.
43. Способы предотвращения возникновения гидравлических ударов Исходя из формулы Жуковского (определяющей увеличение давления при гидроударе) и величин, от которых зависит скорость распространения ударной волны, для ослабления силы этого явления или его полного предотвращения можно уменьшить скорость движения жидкости в трубопроводе, увеличив его диаметр; Для ослабления силы этого явления следует увеличивать время закрытия затвора; Установка демпфирующих устройств.
44. Трубопроводы. Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным или параллельным. Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением или с разветвлениями. В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач. Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.
