Сечение многогранников плоскостью.

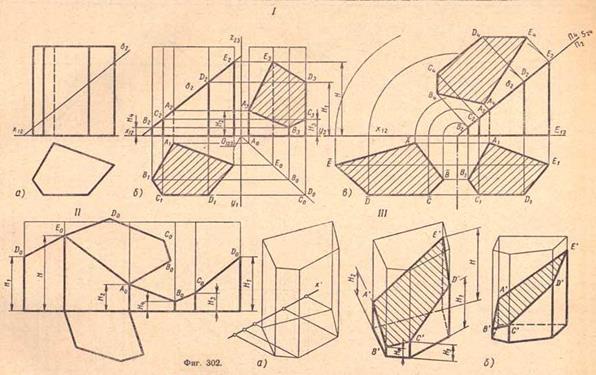
Плоская фигура, полученная при пересечении любого многогранника плоскостью, представляет собой некоторый многоугольник. Вершины этого многоугольника находятся как точки пересечения ребер многогранника с секущей плоскостью, а стороны многоугольника строятся как линии пересечения граней многогранника с секущей плоскостью.

Пересечение поверхностей

Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом:

1. Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого.

2. Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого.

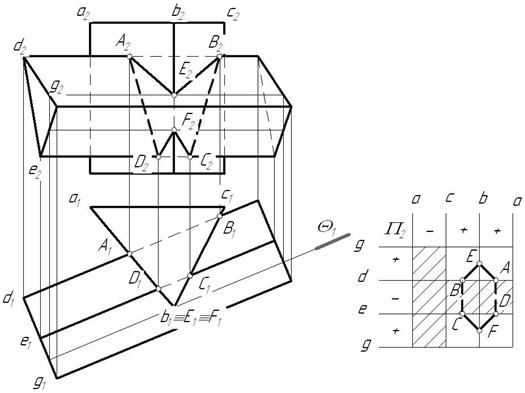
Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая.

В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).

, . , .

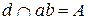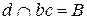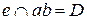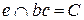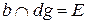
Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость .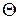

.

Тема11. Развертки

1. Что называют разверткой поверхности?

2. Какие поверхности –разворачивающиеся, а какие- неразворачивающиеся?

3. Укажите основные свойства разверток

4. Что называется аппроксимацией поверхности?

При построении разверток многогранников придется находить действительную величину ребер и граней этих многогранников с помощью вращения или перемены плоскостей проекций. При построении приближенных разверток для неразвертывающихся поверхностей придется заменять участки последних близкими к ним по форме развертывающимися поверхностями.

Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух оснований — многоугольников.

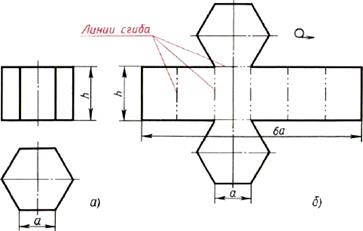Например, у развертки поверхностей шестиугольной призмы (рис. 139, б) все грани — равные между собой прямоугольники шириной а и высотой h, а основания — правильные шестиугольники со стороной, равной а.

Рис. Построение чертежа развертки поверхностей призмы: а — два вида; б — развертка поверхностей

Таким образом, можно построить чертеж развертки поверхностей любой призмы.

Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов (рис. 140, б). Одна сторона прямоугольника равна высоте цилиндра, другая — длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.

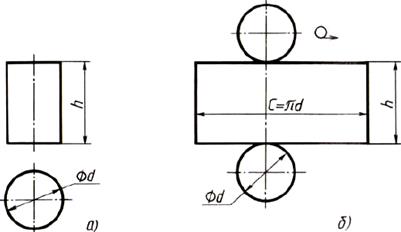
Рис. Построение чертежа развертки поверхностей цилиндра: а - два вида; б - развертка поверхностей

 

Чертежи разверток поверхностей конуса и пирамиды.

Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора - развертки боковой поверхности и круга - основания конуса (рис. 141, 6).

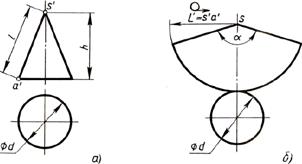
Рис. Построение чертежа развертки поверхностей конуса: а — два вида; б — развертка поверхностей

Построения выполняются так:

 

1. Проводят осевую линию и из точки s' на ней описывают радиусом, равным длине s'a' образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса. Точку s' соединяют с концевыми точками дуги.
2. К полученной фигуре — сектору пристраивают круг. Диаметр этого круга равен диаметру основания конуса.

Длину окружности при построении сектора можно определить по формуле C = 3.14xD.

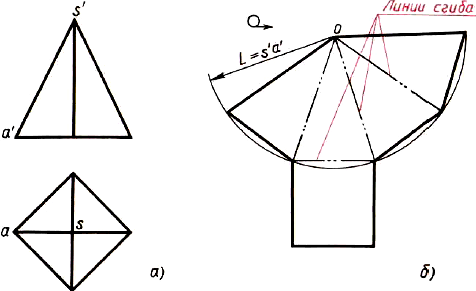Угол а подсчитывают по формуле а = 360°хD/2L, где D — диаметр окружности основания, L —длина образующей конуса, ее можно подсчитать по теореме Пифагора.

Рис. Построение чертежа развертки поверхностей пирамиды: а — два вида; б — развертка поверхностей

Неразвертывающиеся поверхности - поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок.

Приближенные – выполненные способом аппроксимации развертки развертываемых поверхностей (цилиндры, конусы