Гранные поверхности на чертеже

ТЕМА 6. Преобразование комплексного чертежа

ТЕМА 7. Поверхности

Тема 8. Пересечение поверхности проецирующей плоскостью, прямой

ТЕМА 9. Пересечение поверхностей

Тема 10. Многогранники.

1. Какие поверхности называют многогранниками?

2. Какие многогранники называют правильными?

3. Какими элементами задаются многогранники на чертеже?

4. Как построить сечение многогранника плоскостью?

5. Какие два способа построения линии взаимного пересечения многогранников

Гранные поверхности на чертеже

1.К гранным относятся поверхности, образованные перемещением прямолинейной образующей l по ломаной направляющей m. При этом если одна точка S образующей неподвижна, создается пирамидальная поверхность (рис. 97), если образующая при перемещении параллельна заданному направлению S, то создается призматическая поверхность (рис. 98).

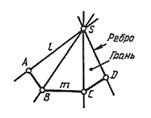
Рис. 97 Пирамидальная поверхностьРис. 98 Призматическая поверхность

Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и конгруэнтные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например: гексаэдр — куб (рис. 99, а), тетраэдр — правильный четырехугольник (рис. 99, 6) октаэдр — многогранник (рис. 99, в). Форму различных многогранников имеют кристаллы.

Рис. 99 Различные многогранники

Пирамида — многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S.

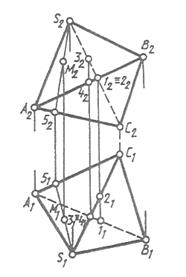На комплексном чертеже пирамида задается проекциями ее вершин и ребер с учетом их видимости. Видимость ребра определяется с помощью конкурирующих точек (рис. 100).

Рис. 100 Видимость ребра

Призма — многогранник, у которого основание — два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы. Если ребра призмы перпендикулярны плоскости основания, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей. На рис. 101 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.

 

Рис. 101 Призма с горизонтально проецирующей поверхностью

При работе с комплексным чертежом многогранника приходится строить на его поверхности линии, а так как линия есть совокупность точек, то необходимо уметь строить точки на поверхности.

Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку. На рис. 100 в грани ACS построена точка М с помощью образующей S-5.

2. Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней. Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 1,а). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.

Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 1,в. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром. Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 1,г. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром. Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильныхтреугольников, то другихправильных многогранников, гранями которых являются правильные треугольники, не существует. Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 1,б), других правильных многогранников, у которых гранями являются квадраты не существует. Куб имеет шесть граней и поэтому называется также гексаэдром. Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 1,д. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром. Поскольку в вершинах выпуклого многогранника не могут сходиться правильные многоугольники с числом сторон больше пяти, то, используя теорему Коши о жесткости выпуклого многогранника, получаем, что других правильных многогранников не существует, и таким образом, имеется только пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.