Векторные линии.
Дифференциальные уравнения
Векторных линий.
Определение 1. Если в каждой точке М пространства или части пространства определена векторная величина а = а(М), то говорят, что задано векторное поле.
Если в пространстве введена декартова система координат, то задание векторного поля
а = а(М) равносильно заданию трёх скалярных функций точки Р(М), Q(M), R(M), так что
а(М) = Р(x,y,z)I + Q(x,y,x)j + R(x,y,z)k.
Определение 2. Векторной линией векторного поля а называется кривая, в каждой точке М которой вектор а направлен по касательной к этой кривой.
Пусть векторное поле определяется вектором
а = Pi + Qj + Rk,
Где
Р = Р(x,y,z), Q = Q(x,y,z), R = R(x,y,z)
- Непрерывные функции от x, y, z, имеющие ограниченные частные производные первого порядка.
Тогда дифференциальные уравненния векторных линий имеют вид
(1)
Интегрированные системы дифференциальных уравнений (1) дает систему двух конечных уравнений
, 
,
Которые, рассматриваемые в совокупности, определяют двухпараметрическое семейство векторных линий
.
Если в некоторой области G для системы (1) выполнены условия теоремы существования и единственности решения, то через каждую точку 
проходит единсвенная векторная линия
Пример 1. Найти векторные линии векторного поля
a = [c, r],
где c – постоянный вектор.
Пример 2. Найти векторную линию поля
a = -yl + xj + bk,
Проходящую через точку (1, 0, 0).
Задачи для самостоятельного решения
Найти векторные линии следующих векторных полей:
92. 
.
93. 
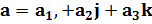, где 
– постоянные.
94. 
н
Найти векторную линию поля
Проходящую через точку 
Пример 3. Найти векторные линии магнитного поля бесконечного проводника тока.
Задачи для самостоятельного решения
Найти векторные линии следующих плоских полей:
96. 
.
97. 
.
98. 
.
99. 
100. 
101. 
Пример 4. Найти векторные линии поля а = {c, r}, где c – постоянный вектор.
Задачи для самостоятельного решения
Найти векторные линии следующих векторных полей:
102. 
103. 
где 
– постоянные векторы.
Поток векторного поля.
Способы вычисления потока.
Определение. Потоком П векторного поля а(М) через ориентированную поверхность S называется поверхностный интеграл первого рода по поверхности S от проекции вектора а(М) на нормаль n(M) к этой поверхности:
Где 
- единичный вектор (орт) нормали n к выбранной стороне поверхности S; dS – элемент площади поверхности S.
Пример 3. Найти поток векторного поля
Через сферу радиуса R с центром в начале координат.
Задачи для самостоятельного решения
104. Вычислить поток векторного поля n = 3j через площадку, имеющую форму треугольника с вершинами в точках 
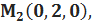
в сторону, где расположено начало координат.
105. Найти поток векторного поля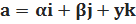 
, где 
– постоянные через площадку, перпендикулярную оси 
и имеющую форму круга радиуса R в положительном направлении оси .
Пример 6. Найти поток векторного поля a = I – J + xyzk через круг S, полученный сечением шара 
плоскостью y=x. Взять сторону круга, обращенную к положительной части оси 
