Ответ на 31 вопрос. Скачки конденсации, тепловые скачки.
Основная идея теории В. А. Андреева и С. 3. Беленького — исследование прямых и косых скачков конденсации как тепловых скачков. Эта теория развита ими применительно к воздуху с небольшим содержанием водяных паров. Изменение массы газа в процессе конденсации считается пренебрежимо малым. Та же теория была применена М. Е. Дейчем [15] для влажного пара. В обоих случаях считается, что при прохождении через скачок полная энтальпия меняется. В уравнении энергии вместо плотности паровой фазы вводится плотность влажного пара. В результате этих допущений были получены простые зависимости между параметрами пара перед скачком и за ним.
Следует особо подчеркнуть, что сейчас анализируются свойства только теплового скачка, а не процессов горения или конденсации в целом. Для анализа задачи в целом необходимы дополнительные сведения о процессе.
Рассмотрим скачок конденсации в предположении 1) пар перед скачком переохлажден и не содержит капелек жидкости 2) насыщенный пар и мелкие капельки жидкости за скачком находятся в тепловом равновесии 3) скорости капелек жидкости за скачком равны скорости пара.
Общее между тепловым скачком и скачком конденсации состоит Б том, что в обоих случаях к потоку подводится теплота. Однако в тепловом скачке эта теплота подводится извне, и поэтому энтальпия торможения после скачка возрастает. В скачке конденсации теплота выделяется при конденсации части текущего пара и поэтому полная энергия потока до и после скачка остается постоянной. Кроме того, различие состоит в том, что после скачка давление и температура связаны условием фазового равновесия. Поэтому количество выделившейся при конденсации теплоты не может быть установлено произвольно, а связано с интенсивностью скачка.
Следует различать конденсационные скачки в одно-, двух- и многокомпонентных средах. В последнем случае в потоке неконденсирующегося газа (или смеси газов) присутствуют пары конденсирующейся среды. Например, пары воды в сверхзвуковом потоке воздуха при определенных условиях спонтанно конденсируются к потоку воздуха подводится скрытая теплота парообразования и его полная энергия (энтальпия торможения) возрастает. Такие скачки иногда называют тепловым и Ч Скачки конденсации в однокомпонентной среде не вызывают изменения энтальпии торможения.
Полученные общие соотношения применимы к любым неадиабатическим скачкам давления вне зависимости от механизма выделения тепла. Мы видели, что в рассмотренных выше двух случаях распространения фронта пламени непосредственно тепловой скачок (т. е. зона горения) представлял как при детонации, так,и при нормальном горении скачок разрежения в дозвуковом течении. Нетрудно указать и случай теплового скачка сжатия в сверхзвуковом потоке. Мы имеем в виду хорошо известные скачки конденсации, сопровождающейся переходом от большей сверхзвуковой скорости к меньшей, но всё ещё сверхзвуковой скорости. И в этом случае приведённые выше уравнения и выводы остаются справедливыми.
Ответ на 55 вопрос. Расчет сверхзвукового сопла
При создании методики расчета сопла приняты следующие допущения:
· газ идеальный, его состояние описывается уравнением Менделеева-Клапейрона;
· расход газа постоянен, течение установившееся;
· газ однороден и неизменен по составу;
· трение между газом и стенками сопла отсутствует;
· теплопередачи через стенки сопла не происходит;
· вязкость и трение между слоями газа пренебрежимо малы;
· скорость газа в поперечном сечении параллельна оси и одинакова во всех точках сечения.
Уравнение движения. Рассмотрим одномерное неустановившееся течение газа в цилиндрической трубе переменного сечения (рис. 1.25). Выделим объем газа между двумя близкими сечениями, находящимися на расстоянии dx. Действие на этот объем стенок трубы и газа слева и справа заменим поверхностными силами, где Р — давление газа, Па; S — площадь поперечного сечения трубы, м².
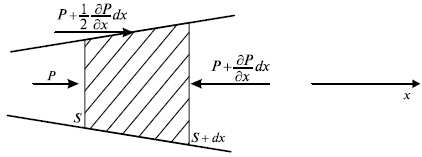
Рис. 1.25. Схема одномерного неустановившегося течения газа в цилиндрической трубе переменного сечения.
Пусть выделенная частица газа объемом Sdx движется вправо под действием поверхностных сил. Второй закон Ньютона для нее записывается следующим образом:
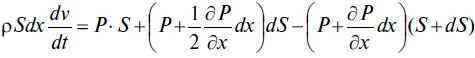где ρ — плотность, кг/м3; ν — скорость газа, м/с.
После несложных преобразований получим:
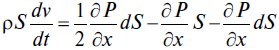
Уравнение неразрывности. Массовый расход газа G [кг/с] в любом сечении трубы постоянен и равен [1.8, 1.9]:
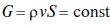(1.18)
Уравнение адиабаты. Уравнение состояния идеального газа (Менделеева-Клапейрона) для единицы массы газа записывается следующим образом:
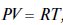(1.22)
где V — удельный объем, м³/кг; R — газовая постоянная (например для воздуха R = 287, Дж/кг град), Р и Т—давление и температура газа соответственно.
В соответствии с первым законом термодинамики элементарное тепло ∂Q, подведенное к газу, идет на изменение внутренней энергии газа dU и совершение этим газом работы:
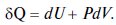(1.23)
Изменение внутренней энергии газа
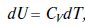(1.24)
где СV —удельная теплоемкость газа в изобарическом процессе, Дж/кг град.
Уравнение энергии. Рассмотрим течение газа в трубе переменного сечения (рис. 1.27) без теплообмена со стенкой. Выбираем некоторый объем газа, ограниченный в начальный момент времени сечениями 1—2. За время dt частицы газа переместятся в новое положение, ограниченное сечениями11—21. Так как течение газа установившееся, то изменения энергии в общем для двух положений объеме между сечениями11—2 не будет, поэтому приращение энергии за время dt вычисляется как разность энергий в объемах1—21 и 1—11.
