В состав автоматических систем часто входят существенно нелинейные элементы, которые существенно изменяют характер системы и придает ей такие свойства, которые никогда не могут быть исследованы в рамках линейной теории. Среди нелинейных элементов автоматических систем особую роль играют так называемые безынерционные нелинейности, не обладающих заметным запаздыванием. Элементарным безынерционным звеном будем называть любую систему, выходная переменная которой в каждый данный момент времени зависит только от значения входной переменной в тот же момент времени и не зависит от того, как изменяется входная переменная до данного момента. Таким образом, оператором элементарного безынерционного звена является обычная функциональная зависимость между входной и выходной переменными. Эта функциональная зависимость называется характеристикой элементарного безынерционного звена. Характеристики элементарных нелинейных звеньев можно разделить на слабые и существенные нелинейности. К первой группе относятся такие нелинейные характеристики, которые при малом диапазоне изменения входного сигнала или при малом его отклонении от изменяющегося среднего значения могут быть заменены линейными. Ко второй группе относятся нелинейные характеристики, которые являются существенно нелинейными функциями, например, разрывными или близкими к разрывным. Зависимость между входной и выходной переменными для таких элементов чаще всего может быть приближенно представлена в виде кусочно-линейных функций.
На рисунке 4.1 представлены характеристики нелинейных элементов, применяемых в работе.

|
Рисунок 4.1- Характеристики НЭ

Для исследования режима автоколебаний составляют и набирают схему модели, соответствующую структурной схеме системы (рисунок 4.2). Амплитуда и частота автоколебаний на входе нелинейного элемента, т.е. на выходе САУ, определяются по осциллографу. Параметры блоков приведены в таблице 4.1.
 Uз Uвых
Uз Uвых

|
Рисунок 4.2- Структурная схема
4.3 Задание для домашней подготовки
4.3.1 По заданным параметрам рассчитать и построить зависимость амплитуды и частоты автоколебаний на выходе САУ от коэффициента усиления линейной части системы.
4.3.2 Проверить выполнение условий применимости гармонической линеаризации для заданных нелинейностей.
4.3.3 Подготовить схемы для моделирования в Matlab Simulink для трех представленных на рисунке 4.2 нелинейностей.
Программа работы
. 4.4.1 Набрать схемы подготовленные при домашней подготовке.
4.4.2 Снять зависимость амплитуды и частоты автоколебаний на выходе САУ от коэффициента усиления линейной части системы. Убедиться в том, что линейная часть является фильтром низких частот.
4.3.3 Сравнить экспериментальные зависимости с расчетными, оценить их совпадение и проанализировать причины их расхождения.
Т а б л и ц а 4.1
| № варианта | Т1, с | Т2, с | Т3, с | Вид нелинейности | U1 U2 | t1 t2 |
| 0.1 | 0.1 | Блок 2,а | - | |||
| 0.1 | Блок 2,а | - | ||||
| 0.2 | 0.1 | 0.1 | Блок 2,а | - | ||
| 0.1 | 0.1 | Блок 2,б | ||||
| 0.1 | Блок 2,б | |||||
| 0.5 | 0.1 | Блок 2,в | - |
Содержание отчета
4.5.1 Цель и программа работы
4.5.2 Структурные схемы САР. Схема модели.
4.5.3 Результаты экспериментов в виде осциллограмм.
4.5.3 Анализ результатов экспериментов. Выводы.
Приложение А
В настоящее время разработано большое число в основном приближенных методов синтеза корректирующих устройств. Наибольшее распространение в инженерной практике получили графо-аналитические методы синтеза, основанные на построении инверсных и логарифмических частотных характеристик разомкнутой системы. При этом широко используются косвенные оценки качества переходного процесса не требующие решения системы дифференциальных уравнений, такие как запас по фазе, запас по модулю, колебательность, частота среза, которые можно непосредственно определить по частотным характеристикам.
К другой группе относятся аналитические методы синтеза. Для них находятся выражения, аналитически связывающие показатели качества системы с параметрами корректирующего устройства, и определяются значения параметров, соответствующих экстремальному значению функции.
К этим методам относится синтез системы по интегральным критериям качества переходного процесса и критерию среднеквадратичной ошибки.
Применение современных средств вычислительной техники снимает трудности, связанные с непосредственным решением дифференциальных уравнений и построением переходных процессов. В связи с этим наблюдается тенденция решать задачу не приближенными методами, а путем направленного перебора решений исходной системы дифференциальных уравнений при вариации интересующих исследователя параметров корректирующего устройства.
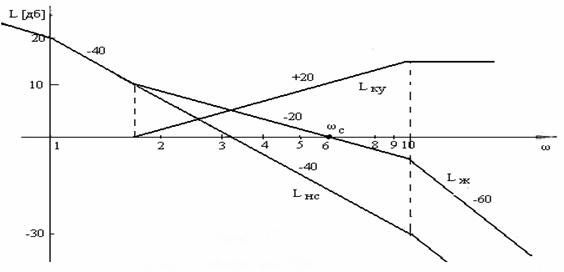
Рассмотрим подробнее удобный из графо-аналитических методов синтеза -метод логарифмических амплитудных характеристик. Он применяется для синтеза минимально-фазовых САР, у которых имеется однозначная связь между амплитудной и фазовой частотной характеристиками.
Процесс синтеза включает в себя следующие этапы:
- строится ЛАЧХ исходной нескорректированной системы LНС(ω) с учетом требуемого коэффициента усиления системы КР в разомкнутом состоянии, который выбирается исходя из условия обеспечения заданной точности системы в установившемся режиме;
-по заданным показателям качества -перерегулированию σmax, времени регулирования строится желаемая ЛАЧХ системы LЖ(ω);
-вычитанием ординат желаемой ЛАЧХ ординат ЛАЧХ исходной нескорректированной системы определяют ЛАЧХ корректирующего устойства LК(ω);
- по полученной LК(ω) находится WK(p) и подбирается наиболее простой способ технической реализации.
Пусть передаточная функция нескорректированной следящей системы в разомкнутом состоянии

где Т1=1с; Т2=0,1с; КР=10.
Соответствующая ей структурная схема

Рисунок 1-Структурная схема
Требуется обеспечить следующие показатели качества: перерегулирование  ;
; 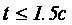 .
.
Проведем синтез последовательного корректирующего устройства.
Построим ЛАЧХ разомкнутой нескорректированной системы. Для этого находим  и сопрягающие частоты (см.рисунок 4):
и сопрягающие частоты (см.рисунок 4):  .
.
Для построения желаемой ЛАЧХ, LЖ, находим частоту среза  .
.
Находим ЛАЧХ корректирующего устройства, как  .
.
Определим передаточную функцию и блок схему реализации КУ
|
 .
.
Рисунок 2- Логарифмические частотные характеристики
Список литературы
1. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования.-М.: Наука, 1977.
2.Теория автоматического управления. Под ред. А.А.Воронова. - М.: Высшая школа, 1977.
3. Теория автоматического управления: учебник для вузов / под ред. Ю.М.Соломенцева. - М.: Высшая школа, 1999.
4. Топчеев Ю.И., Цыпляков А.П. Задачник по теории автоматического регулирования. -М.: Машиностроение, 1977.
5. Сборник задач по теории автоматического регулирования и управления. Под ред. Бесекерского В.А. -М.: Машиностроение, 1972.
6. Теория автоматического управления. Учебник для ВУЗов/Под ред. Нетушила А.В. М.: "Высшая школа", 1976.
Содержание
1 Лабораторная работа № 1……………………………………………… 3
2 Лабораторная работа № 2……………………………………………… 7
3 Лабораторная работа № 3……………………………………………….9
4 Лабораторная работа № 4……………………………………………… 11
Приложение А……………………………………………………………..14






