Завдання 1 (0,1 балів за кожну)
1. Що називають аналітичною механікою?
а) розділ механіки, в якому вивчаються загальні методи роз взування динамічних задач для довільної системи матеріальних точок;
б) розділ механіки, в якому вивчаються характер і причини руху для невільної системи матеріальних точок;
в) розділ механіки, в якому вивчаються загальні методи роз взування задач для невільної системи матеріальних точок.
2. Запишіть диференціальне рівняння голономного зв’язку.
а)  ; б)
; б) 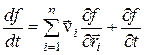 ; в)
; в)  .
.
3. Яку систему рівнянь називають рівняннями Лагранжа першого роду?
а) систему рівнянь, з яких одночасно визначаються координати точок і сили реакції зв’язків;
б) систему рівнянь, які дозволяють знайти закон руху невільної системи матеріальних точок;
в) систему рівнянь, яка встановлює умови рівноваги голономних систем із стаціонарними стримуючими зв’язками.
4. Яку систему рівнянь називають рівняннями Лагранжа другого роду?
а) систему рівнянь, з яких одночасно визначаються координати точок і сили реакції зв’язків;
б) систему рівнянь, які дозволяють знайти закон руху невільної системи матеріальних точок;
в) систему рівнянь, яка встановлює умови рівноваги голономних систем із стаціонарними стримуючими зв’язками.
5. Які переміщення точок системи називають можливими?
а) нескінчено малі переміщення точок системи, що пов’язані з обмеженнями збоку зв’язків; б) нескінчено малі переміщення точок системи, що пов’язані із обмеженнями з боку зв’язків та задовольняють диференціальному рівнянню руху такої системи; в) будь-які малі переміщення точок системи, що задовольняють накладеним на систему зв’язкам при фіксованому моменті часу.
6. Які переміщення називають дійсними?
а) нескінчено малі переміщення точок системи, що пов’язані з обмеженнями збоку зв’язків; б) нескінчено малі переміщення точок системи, що пов’язані із обмеженнями з боку зв’язків та задовольняють диференціальному рівнянню руху такої системи; в) будь-які малі переміщення точок системи, що задовольняють накладеним на систему зв’язкам при фіксованому моменті часу.
7. Які переміщення називають віртуальними?
а) нескінчено малі переміщення точок системи, що пов’язані з обмеженнями збоку зв’язків; б) нескінчено малі переміщення точок системи, що пов’язані із обмеженнями з боку зв’язків та задовольняють диференціальному рівнянню руху такої системи; в) будь-які малі переміщення точок системи, що задовольняють накладеним на систему зв’язкам при фіксованому моменті часу.
8. Записати правило розрахунку варіацій функції.
а)  ; б)
; б)  ; в)
; в)  .
.
9. Записати постулат ідеальності зв’язків.
а)  ; б)
; б)  ; в)
; в)  .
.
10. Сформулювати принцип віртуальних переміщень.
а) для рівноваги будь-якої механічної системи з голономними, стаціонарними, ідеальними та стримуючими зв’язками необхідно і достатньо, щоб сума віртуальних робіт всіх активних сил, діючих на систему, була б рівною нулю при будь-якому її віртуальному переміщенні;
б) для рівноваги будь-якої механічної системи з голономними, стаціонарними, ідеальними та стримуючими зв’язками необхідно і достатньо, щоб сума віртуальних робіт всіх активних і пасивних сил, діючих на систему, була б рівною нулю при будь-якому її віртуальному переміщенні;
в) для рівноваги будь-якої механічної системи з голономними, стаціонарними, ідеальними та стримуючими зв’язками необхідно і достатньо, щоб сума віртуальних робіт всіх сил реакції зв’язків, діючих на систему, була б рівною нулю при будь-якому її віртуальному переміщенні;
11. Які координати називають узагальненими?
а)  величин, які однозначно визначають положення системи
величин, які однозначно визначають положення системи  матеріальних точок, рух, якої обмежений
матеріальних точок, рух, якої обмежений  зв’язками;
зв’язками;
б)  величин, які однозначно визначають положення системи
величин, які однозначно визначають положення системи  матеріальних точок, рух, якої обмежений
матеріальних точок, рух, якої обмежений  зв’язками;
зв’язками;
в)  величин, які однозначно визначають положення системи
величин, які однозначно визначають положення системи  матеріальних точок, рух, якої обмежений
матеріальних точок, рух, якої обмежений  зв’язками
зв’язками
12. Як визначається узагальнена сила, що відповідає узагальненій координаті  ?
?
а)  ; б)
; б)  ; в)
; в)  .
.
13. Записати принцип віртуальних переміщень в узагальнених координатах.
а)  ; б)
; б)  ; в)
; в)  .
.
14. Записати умову рівноваги механічної системи у потенціальному силовому полі.
а)  ; б)
; б)  ; в)
; в)  .
.
15. Перелічити чотири існуючи типи рівноважних станів системи.
а) стійка, нестійка, байдужа, потенціальна; б) стійка, нестійка, рівноважна, нерівноважна; в) стійка, нестійка, байдужа, сідлоподібна.
16. Сформулювати принцип Д’аламбера.
а) геометрична сума д’аламберівських сил реакції зв’язків, що задають рівноважний стан системи, рівна нулю; б) якщо до заданих сил добавити сили, що рівні д’аламберівським силам інерції, то отримана система буде знаходитись у рівновазі; в) якщо до заданих сил та сил реакції добавити сили, що рівні силам інерції, то отримана система буде знаходитись у рівновазі.
17. Сформулювати принцип Д’аламбера-Лагранжа.
а) У будь-який момент часу руху механічної системи, алгебраїчна сума віртуальних робіт заданих сил та д’аламберівських сил інерції дорівнює нулю, якщо рух системи обмежених стримуючими, голономними та ідеальними зв’язками.
б) У будь-який момент часу руху механічної системи, якщо до заданих сил та сил реакції добавити сили, що рівні силам інерції, то отримана система буде знаходитись у рівновазі.
в) У будь-який момент часу руху механічної системи, геометрична сума віртуальних робіт заданих сил, сил реакції зв’язків та д’аламберівських сил інерції дорівнює нулю, якщо розглядувана система перебуватиме у рівноважному стані.
18. Що називають узагальненою швидкістю?
а) векторну величину, що визначається як  ;
;
б) векторну величину, що визначається як 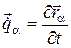 ;
;
в) скалярну величину, що визначається як  ;.
;.
19. Записати рівняння Лагранжа другого роду в узагальнених координатах у довільному зовнішньому полі.
а)  ; б)
; б)  ; в)
; в)  .
.
20. Записати рівняння Лагранжа другого роду в узагальнених координатах у потенціальному зовнішньому полі.
а)  ; б)
; б)  ; в)
; в)  .
.
21. Як задається функція Лагранжа?
а)  ; б)
; б)  ; в)
; в)  .
.
22. Як задається функція Гамільтона?
а)  ; б)
; б) 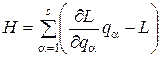 ; в)
; в) 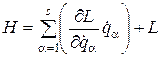 .
.
23. Сформулювати закон збереження узагальненої енергії.
а) якщо функція Лагранжа від часу явно не залежить, то узагальнена енергія з часом зберігається; б) повний диференціал від функції Гамільтона, що описує рух системи визначається частковою похідною від лагранжіана системи за часом і зберігається; в) якщо зв’язки, що обмежують рух системи стаціонарні та стаціонарні зовнішні силові поля, тоді функція Лагранжа явно від часу не залежить, а функція Гамільтона зберігається.
24. Сформулювати теорему про зміну узагальненої енергії.
а) якщо функція Лагранжа від часу явно не залежить, то узагальнена енергія з часом не змінюєься; б) повний диференціал від функції Гамільтона, що описує рух системи визначається частковою похідною від лагранжіана системи за часом, взятий із знаком „-„ в) якщо зв’язки, що обмежують рух системи стаціонарні та стаціонарні зовнішні силові поля, тоді функція Лагранжа явно від часу не залежить і не змінюється.
25. Що називають узагальненим імпульсом?
а)  ; б)
; б)  ; в)
; в)  .
.
26. Як функція Гамільтона повоза з кінетичною і потенціальною енергією системи?
а)  ; б)
; б) 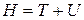 ; в)
; в)  .
.
27. Які координати називають циклічними?
а) узагальнені координати, що описують стан системи, але від яких лагранжіан системи явно не залежить; б) узагальнені координати, що описують стан системи, але від яких гамільтоніан системи явно не залежить; в) узагальнені координати, що описують стан системи, але від яких кінетична енергія системи явно не залежить.
28. Який математичний вигляд мають рівняння Гамільтона?
а)  ; б)
; б)  ; в)
; в)  .
.
29. Яке поле називають центрально-симетричним?
а) центрально-симетричне поле – це поле, в якому потенціальна енергія є функцією обернено пропорційною віддалі від нерухомого центра до рухомої матеріальної точки, т. т.  ;
;
б) центрально-симетричне поле – це поле, в якому потенціальна енергія є функцією, що задається радіус-вектором від нерухомого центра до рухомої матеріальної точки, т. т.  ;
;
в) центрально-симетричне поле – це поле, в якому потенціальна енергія є функцією лише від віддалі від нерухомого центра до рухомої матеріальної точки, т. т.  .
.
30. Що являє собою перший векторний інтеграл руху частинки у ЦСП?
а) 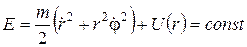 ; б)
; б)  ; в)
; в)  .
.
31. Що називають ефективним потенціалом?
а) 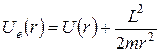 ; б)
; б)  ; в)
; в)  .
.
32. Як визначається секторна швидкість руху частинки у ЦСП?.
а)  ; б)
; б) 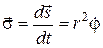 ; в)
; в)  .
.
33. Що являє собою задача про рух в полі сил тяжіння.
а) Задача про рух двох частинок, які взаємодіють за законом  ;
;
б) Задача про рух двох частинок, які взаємодіють за законом  ;
;
в) Задача про рух двох частинок, які взаємодіють за законом  .
.
34. Сформулювати перший закон Кеплера.
а) Всі планети рухаються навколо Сонця по еліпсах, в одному з фокусів якого знаходиться Сонце. б) Всі планети рухаються навколо Сонця по еліпсах, в одному з фокусів якого знаходиться центр мас системи ”планета-Сонце”. в) Земля рухається навколо Сонця по колу, в центрі якого знаходиться Сонце.
35. Сформулювати другий закон Кеплера.
а) Радіус-вектор планети за рівні проміжки часу описують рівні площі. б) Всі планети рухаються навколо Сонця по еліпсах, в одному з фокусів якого знаходиться центр мас системи ”планета-Сонце”. в) Квадрати періодів планет відносяться до кубів півосей для всіх планет майже однаково.
36. Сформулювати третій закон Кеплера.
а) Радіус-вектор планети за рівні проміжки часу описують рівні площі. б) Всі планети рухаються навколо Сонця по еліпсах, в одному з фокусів якого знаходиться центр мас системи ”планета-Сонце”. в) Квадрати періодів планет відносяться до кубів півосей для всіх планет майже однаково.
37. На графіку зображено залежність ефективного потенціалу руху тіла від віддалі до силового центру:

Якому значенню повної енергії частинки та її віддалі до силового центру відповідатиме інфінітний рух гіперболічної траєкторії?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
.
38. На графіку зображено залежність ефективного потенціалу руху тіла від віддалі до силового центру:

Якому значенню повної енергії частинки та її віддалі до силового центру відповідатиме інфінітний рух параболічної траєкторії?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
.
39. На графіку зображено залежність ефективного потенціалу руху тіла від віддалі до силового центру:

Якому значенню повної енергії частинки та її віддалі до силового центру відповідатиме фінітний рух еліптичної траєкторії?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
.
40. На графіку зображено залежність ефективного потенціалу руху тіла від віддалі до силового центру:

Якому значенню повної енергії частинки та її віддалі до силового центру відповідатиме фінітний рух по колу?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
.
41. Що являє собою задача двох тіл?
а) Задача про рух двох частинок, що взаємодіють між собою, зводиться до задачі одного тіла і розв’язується повністю, може бути зведена до двох задач (одночастинних): задачі про рух центру мас; рух точки зведеної маси відносно центру мас.
б) Задача про рух двох частинок, що взаємодіють між собою, зводиться до задачі одного тіла і розв’язується повністю, може бути зведена до одночастинної задачі про рух центру мас такої взаємодіючої системи.
в) Задача про рух двох частинок, що взаємодіють між собою, зводиться до задачі одного тіла і розв’язується повністю, може бути зведена до одночастинної задачі про рух точки зведеної маси відносно центру мас такої взаємодіючої системи.
42. Що називають зведеною масою?
а)  ; б)
; б)  ; в)
; в)  .
.
43. Що називають 2-ою космічною швидкістю?
а) 
 км/с; б)
км/с; б) 
 км/с; в)
км/с; в) 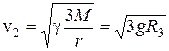
 км/с.
км/с.
44. Що називають 1-ою космічною швидкістю?
а) 
 км/с; б)
км/с; б) 
 км/с; в)
км/с; в) 
 км/с.
км/с.
45. Що називають 3-ою космічною швидкістю, яке її мінімальне значення?
а)  км/с; б)
км/с; б)  км/с; в)
км/с; в)  км/с.
км/с.
46. Записати рівняння траєкторії точки, що рухається під дією центральної сили.
а)  ; б)
; б)  ; в)
; в) 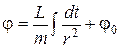 .
.
47. Що називають одновимірним гармонійним осцилятором?
а) одновимірний рух частинки масою  в полі сил, потенціал якої
в полі сил, потенціал якої  має мінімум у точці
має мінімум у точці 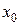 ; б) одновимірний рух частинки масою
; б) одновимірний рух частинки масою  в полі сил, потенціал якої
в полі сил, потенціал якої  має мінімум у точці
має мінімум у точці 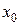 ; в) рух частинки масою
; в) рух частинки масою  в полі сил, потенціал якої
в полі сил, потенціал якої  має мінімум у точці
має мінімум у точці  .
.
48. Записати лінійне диференціальне рівняння руху осцилятора.
а)  ; б)
; б)  ; в)
; в)  .
.
49. Записати загальний розв’язок рівняння затухаючих коливань осцилятора.
а)  ; б)
; б)  ; в)
; в)  .
.
50. Записати загальний розв’язок рівняння гармонійних коливань осцилятора.
а)  ; б)
; б)  ; в)
; в)  .
.
51. Записати закон збереження енергії для механічного осцилятора.
а) 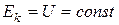 ; б)
; б)  ; в)
; в)  .
.
52. У якому випадку коливання механічної системи можна вважати малими?
а) коли кут відхилення коливальної системи від положення рівноваги малий; б) коли потенціальна енергія коливальної системи не змінюється; в) коли кінетична енергія коливальної системи у положенні рівноваги максимальна.
53. Як визначається період гармонійних коливань осцилятора?
а) 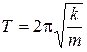 ; б)
; б)  ; в)
; в)  .
.
54. Як визначається логарифмічний декримент затухання коливального процесу?
а)  ; б)
; б)  ; в)
; в)  .
.
55. Чому дорівнюють амплітуда коливань осцилятора?
а)  ; б)
; б)  ; в)
; в)  .
.
56. Який рух частинки називають одновимірним?
а) той, що визначається лише однією координатою; б) той, що обумовлює її рух одновимірним потенціальним полем; в) той, що задається одновимірним диференціальним рівнянням її руху.
57. Яку силу називають вимушеною?
а) зовнішню періодичну силу, що діє на коливальну систему; б) внутрішню аперіодичну силу, що діє у коливальній системі; в) зовнішню силу, що виводить коливальну систему із її положення рівноваги.
58. Як визначається резонансна частота вільних коливань осцилятора?
а) 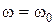 ; б)
; б)  ; в)
; в)  .
.
59. Як визначається резонансна частота коливань осцилятора за наявності сили в’язкого тертя?
а) 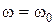 ; б)
; б)  ; в)
; в)  .
.
60. Яке явище називають резонансом?
а) Явище, яке полягає в тому, що при певному значенні частоти зовнішньої сили, амплітуда коливань набуває мінімального значення. б) Явище, яке полягає в тому, що при певному значенні частоти зовнішньої сили, амплітуда коливань набуває оптимального значення. в) Явище, яке полягає в тому, що при певному значенні частоти зовнішньої сили, амплітуда коливань набуває максимального значення.
61. Що називають шириною резонансної кривої?
а) ширину резонансу характеризують віддалю  вздовж вісі абсцис; б) ширину резонансу характеризують віддалю
вздовж вісі абсцис; б) ширину резонансу характеризують віддалю  вздовж вісі ординат; в)
вздовж вісі ординат; в) 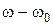 .
.
62. Що називають добротністю коливальної системи?
а)  ; б)
; б)  ; в)
; в) 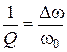 .
.
63. Що називають биттям?
а) періодична передача імпульсів коливань від одного коливального маятника до іншого зв’язаної коливальної системи; б) періодичне перекачування енергії від одного коливального маятника до іншого зв’язаної коливальної системи; в) періодична зміна періоду коливань маятників, від одного до іншого, зв’язаної коливальної системи.
Завдання 2 (0,5 балів за кожну)
1. Яку мінімальну швидкість необхідно надати космічному апарату на поверхні планети, що він віддалився від неї на нескінченість? Розрахунки виконати для Землі, Місяця, Марса, Венери й Юпітера. Використати таблицю.
| Планета | 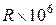 , м , м
|  , кг , кг
|  , км/с , км/с
|  , с , с
|
| Земля | 6,37 | 
| 7,91 | |
| Місяць | 1,737 | 
| 1,68 | |
| Венера | 6,05 | 0,815 
| 7,3 | |
| Марс | 2,44 | 0,055 
| 3,54 | |
| Юпітер | 69,9 | 318 
| 42,6 |
2. Яку мінімальну початкову швидкість необхідно надати космічному апарату біля поверхні Землі, що він міг покинути межі Сонячної системи?
Відповідь:16,7 км/с.
Завдання 3 (1 бал за кожну)
1. Тіло, що підвисили на двох вертикальних нитках довжиною  кожна, віддаль між якими
кожна, віддаль між якими  , закручується навколо вертикальної вісі, що лежить у площині ниток та рівновіддаленої від них (біфілярний підвіс). Радіус інерції тіла відносно вісі обертання
, закручується навколо вертикальної вісі, що лежить у площині ниток та рівновіддаленої від них (біфілярний підвіс). Радіус інерції тіла відносно вісі обертання  . Відшукати період малих коливань.
. Відшукати період малих коливань.
Відповідь:  .
.
2. Визначити період малих вільних коливань маятника масою  , Віль обертання якого утворює кут
, Віль обертання якого утворює кут  із горизонтальною площиною. Момент інерції маятника відносно вісі обертання
із горизонтальною площиною. Момент інерції маятника відносно вісі обертання  , віддаль центру мас від вісі обертання
, віддаль центру мас від вісі обертання  .
.
Відповідь:  .
.






