Розділ “Алгебричні структури”
I. Виконайте завдання.
1) Задано множину  цілих чисел, які при діленні на 3 дають остачу 2, і операцію звичайного віднімання (–). Дослідіть, чи утворюють множина
цілих чисел, які при діленні на 3 дають остачу 2, і операцію звичайного віднімання (–). Дослідіть, чи утворюють множина  і операція (–) алгебру. Якщо так, то класифікуйте алгебричну структуру
і операція (–) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
2) Нехай  — множина всіх квадратних невироджених матриць порядку n, елементами яких є дійсні числа,
— множина всіх квадратних невироджених матриць порядку n, елементами яких є дійсні числа,  — операція множення матриць. Дослідіть, чи утворюють множина
— операція множення матриць. Дослідіть, чи утворюють множина  і операція
і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
3) Задано множину комплексних чисел  і операцію звичайного множення (
і операцію звичайного множення ( ). Дослідіть, чи утворюють множина А і операція (
). Дослідіть, чи утворюють множина А і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
4) Задано множину раціональних чисел без нуля  і операцію звичайного множення (
і операцію звичайного множення ( ). Дослідіть, чи утворюють множина А і операція (
). Дослідіть, чи утворюють множина А і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру 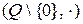 , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
5) Дослідіть, чи утворюють множина ірраціональних чисел  і операція звичайного додавання (
і операція звичайного додавання ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
6) Задано множину Z цілих чисел і операцію  , яка визначається так:
, яка визначається так:  . Дослідіть, чи утворюють множина Z і операція
. Дослідіть, чи утворюють множина Z і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
7) Задано множину N натуральних чисел і операцію  , яка визначається так:
, яка визначається так:  . Дослідіть, чи утворюють множина N і операція
. Дослідіть, чи утворюють множина N і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
8) Задано множину додатних раціональних чисел  , де
, де  — нескоротний дріб, і операцію звичайного множення (
— нескоротний дріб, і операцію звичайного множення ( ). Дослідіть, чи утворюють множина
). Дослідіть, чи утворюють множина  і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
9) Нехай  — множина n -вимірних векторів з дійсними координатами, (+) — операція покоординатного додавання векторів. Дослідіть, чи утворюють множина
— множина n -вимірних векторів з дійсними координатами, (+) — операція покоординатного додавання векторів. Дослідіть, чи утворюють множина  і операція (+) алгебру. Якщо так, то класифікуйте алгебричну структуру
і операція (+) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
10) Нехай  — множина раціональних чисел з проміжку
— множина раціональних чисел з проміжку  , у яких дробова частина містить n цифр (наприклад, при
, у яких дробова частина містить n цифр (наприклад, при  такими числами є:
такими числами є:  ,
,  ), (+) — операція звичайного додавання. Дослідіть, за якої умови алгебрична структура
), (+) — операція звичайного додавання. Дослідіть, за якої умови алгебрична структура  є абелевою (комутативною) групою.
є абелевою (комутативною) групою.
11) Нехай  — множина всіх парних цілих чисел, (
— множина всіх парних цілих чисел, ( ) — операція звичайного множення. Дослідіть, чи утворюють множина
) — операція звичайного множення. Дослідіть, чи утворюють множина  і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
12) Задано множину комплексних чисел  і операцію звичайного додавання (+). Дослідіть, чи утворюють множина А і операція (+) алгебру. Якщо так, то класифікуйте алгебричну структуру
і операцію звичайного додавання (+). Дослідіть, чи утворюють множина А і операція (+) алгебру. Якщо так, то класифікуйте алгебричну структуру 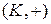 , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
13) Дослідіть, чи утворюють множина натуральних чисел N і операція звичайного додавання (+) алгебру. Якщо так, то класифікуйте алгебричну структуру 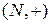 , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
14) Задано множину 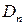 визначників квадратних матриць порядку n і операцію множення матриць (
визначників квадратних матриць порядку n і операцію множення матриць ( ). Дослідіть, чи утворюють множина
). Дослідіть, чи утворюють множина 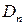 і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
15) Дослідіть, чи утворюють множина цілих чисел Z і операція звичайного віднімання (–) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
16) Дослідіть, чи утворюють множина раціональних чисел Q і операція звичайного ділення (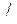 ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру 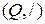 , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
17) Задано множину натуральних чисел N і для будь-яких елементів  визначено бінарну операцію
визначено бінарну операцію  як модуль різниці цих елементів
як модуль різниці цих елементів  . Дослідіть, чи утворюють множина N і операція
. Дослідіть, чи утворюють множина N і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
18) Дослідіть, чи утворюють множина натуральних чисел N і операція звичайного множення ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
19) Задано множину натуральних чисел N і для будь-яких елементів  визначено бінарну операцію
визначено бінарну операцію  як менший із цих елементів
як менший із цих елементів  . Дослідіть, чи утворюють множина N і операція
. Дослідіть, чи утворюють множина N і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
20) Задано множину комплексних чисел  (де Q — множина раціональних чисел) і операцію ділення (
(де Q — множина раціональних чисел) і операцію ділення (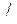 ). Класифікуйте алгебричну структуру
). Класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
21) Дослідіть, чи утворюють множина ірраціональних чисел  і операція звичайного множення (
і операція звичайного множення ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
22) Задано множину ненульових комплексних чисел  і операцію множення (
і операцію множення ( ). Дослідіть, чи утворюють множина А і операція (
). Дослідіть, чи утворюють множина А і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
23) Задано множину  визначників невироджених квадратних матриць порядку n і операцію множення матриць (
визначників невироджених квадратних матриць порядку n і операцію множення матриць ( ). Дослідіть, чи утворюють множина
). Дослідіть, чи утворюють множина  і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
24) Задано множину Z цілих чисел і операцію  , яка визначається так:
, яка визначається так:  . Дослідіть, чи утворюють множина Z і операція
. Дослідіть, чи утворюють множина Z і операція  алгебру. Якщо так, то класифікуйте алгебричну структуру
алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
25) Задано множину  натуральних чисел, які при діленні на 3 дають остачу 1, і операцію звичайного множення (
натуральних чисел, які при діленні на 3 дають остачу 1, і операцію звичайного множення ( ). Дослідіть, чи утворюють множина
). Дослідіть, чи утворюють множина  і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
26) Задано множину  і операцію додавання за модулем 4 (
і операцію додавання за модулем 4 ( ; при цьому операція додавання за модулем m
; при цьому операція додавання за модулем m 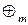 визначається так:
визначається так: 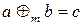 , де
, де  ,
,  ,
,  ,
,  ). Дослідіть, чи утворюють множина
). Дослідіть, чи утворюють множина  і операція (
і операція ( ) алгебру. Якщо так, то класифікуйте алгебричну структуру
) алгебру. Якщо так, то класифікуйте алгебричну структуру  , дослідивши її основні властивості й існування одиничного та оберненого елементів.
, дослідивши її основні властивості й існування одиничного та оберненого елементів.
Розділ “Алгебра логіки”
II. Використовуючи таблицю істинності, доведіть чи спростуйте тотожність.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 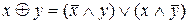 ;
;
7)  ; 8)
; 8) 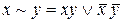 ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20)  ;
;
21)  ; 22)
; 22)  ;
;
23)  ; 24)
; 24) 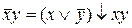 ;
;
25)  ; 26)
; 26)  .
.
III. Запишіть формулу функції, двоїстої до заданої функції  , використовуючи а) означення двоїстої функції; б) принцип двоїстості.
, використовуючи а) означення двоїстої функції; б) принцип двоїстості.
1) 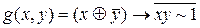 ; 2)
; 2) 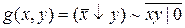 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9) 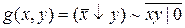 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ;
;
17) 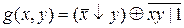 ; 18)
; 18)  ;
;
19)  ; 20)
; 20)  ;
;
21)  ; 22)
; 22)  ;
;
23)  ; 24)
; 24)  ;
;
25)  ; 26)
; 26)  .
.
IV. Для заданої функції  запишіть: а) ДДНФ; б) ДКНФ; в) поліном Жегалкіна; в) дослідіть, чи є функція самодвоїстою.
запишіть: а) ДДНФ; б) ДКНФ; в) поліном Жегалкіна; в) дослідіть, чи є функція самодвоїстою.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20)  ;
;
21)  ; 22)
; 22)  ;
;
23)  ; 24)
; 24)  ;
;
25)  ; 26)
; 26)  .
.
V. Обґрунтовуючи належність кожної функції поданої системи до певного класу Поста і використовуючи критерій Поста, дослідіть, чи є повною система функцій.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12) 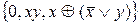 ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20)  ;
;
21)  ; 22)
; 22)  ;
;
23) 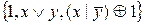 ; 24)
; 24) 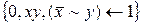 ;
;
25)  ; 26)
; 26)  .
.
VI. Для заданої функції  знайдіть скорочену ДНФ: а) методом Квайна; б) за допомогою діаграм Хассе.
знайдіть скорочену ДНФ: а) методом Квайна; б) за допомогою діаграм Хассе.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 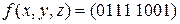 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13) 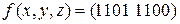 ; 14)
; 14) 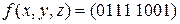 ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20) 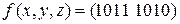 ;
;
21)  ; 22)
; 22)  ;
;
23)  ; 24)
; 24) 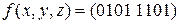 ;
;
25)  ; 26)
; 26)  ;
;
VII. Для функції  знайдіть мінімальну ДНФ за допомогою карт Карно.
знайдіть мінімальну ДНФ за допомогою карт Карно.
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11)  ;
;
12)  ;
;
13)  ;
;
14)  ;
;
15)  ;
;
16)  ;
;
17)  ;
;
18)  ;
;
19)  ;
;
20)  ;
;
21)  ;
;
22) 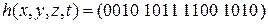 ;
;
23)  ;
;
24)  ;
;
25) 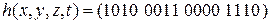 ;
;
26)  .
.
Розділ “Математична логіка”
VIII. У відповідність складному висловлюванню поставте формулу, виділивши перед цим прості висловлювання і заміняючи зв’язки логічними операціями. Перевірте, чи є одержана формула тавтологією.
1) “Якщо число ділиться на 6, то воно ділиться на 2 і на 3”;
2) “Буде чи не буде дощ, я піду на заняття або в бібліотеку”;
3) “Я роздрукую завдання тоді і тільки тоді, коли матиму папір і заправлю картридж”;
4) “Зображення буде чітким, якщо при скануванні задати велику роздільну здатність, а при збереженні використати алгоритм стискання без втрати якості”;
5) “Я добре засвою матеріал, якщо розберу теорію і виконаю практичні завдання”;
6) “Якщо дощ буде лити як з відра, то я не піду ні на заняття, ні в бібліотеку”;
7) “Сьогодні ми склали іспит, тому завтра будемо відпочивати і милуватися природою”;
8) “Якщо я проснуся і буде лити дощ, то я на заняття не піду”;
9) “Ноутбук буде працювати, якщо буде напруга в мережі або буде заряджений акумулятор”;
10) “Якщо буде бажання, то влітку ми поїдемо в гори або на море”;
11) “Я підготуюся до складного іспиту, якщо буде хороший конспект і багато книжок”;
12) “Я піду на прогулянку тоді і тільки тоді, коли закінчаться заняття і буде хороша погода”;
13) “Якщо в картриджі буде тонер, то я роздрукую реферат і розв’язки задач”;
14) “Коли настане літо і закінчиться сесія, студенти будуть мати великі канікули”;
15) “Ми зможемо скласти залік тоді і тільки тоді, коли виконаємо всі лабораторні роботи і успішно їх захистимо;
16) “Вночі студент писав програму і робив завдання з дискретної математики і тому вранці пізно прокинувся”;
17) “Якщо я буду мати час, то напишу програму, але не буду виконувати завдання з дискретної математики”;
18) “Я напишу хорошу програму тоді і тільки тоді, коли буде натхнення або матиму багато часу”;
19) “Якщо в комп’ютері малий обсяг оперативної пам’яті або слабка відеокарта, то комп’ютер буде працювати повільно”;
20) “Розклад занять буде оптимальний тоді і тільки тоді, коли в ньому не буде “вікон” і щодня буде однакова кількість пар”;
21) “Якщо процесор перегріється, то комп’ютер буде працювати некоректно або навіть зависне”;
22) “Подання інформації буде структурованим, якщо використати списки або таблиці”;
23) “Якщо число закінчується на 0, то воно ділиться на 2 і на 5”;
24) “Програмний код зрозумілий тоді і тільки тоді, коли він поданий структуровано і в ньому є коментарі”;
25) “Якщо в чотирикутнику всі кути рівні, то він є прямокутником або квадратом”;
26) “Студент правильно виконає домашнє завдання тоді і тільки тоді, коли він розбере теорію і зрозуміє подані на занятті приклади”.
IX. Визначте, за допомогою якого правила виведення системи природного виведення можна довести подану нижче теорему. Якщо при цьому є засновок, який не використовується для одержання висновку, то вкажіть його.
1) “Із А, В,  одержати
одержати  ”; (
”; ( )
)
2) “Із  ,
,  одержати
одержати  ”; (
”; (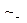 )
)
3) “Із  ,
, 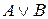 одержати
одержати 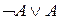 ”; (
”; ( )
)
4) “Із  ,
, 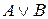 одержати
одержати  ”; (
”; (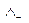 )
)
5) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
6) “Із  ,
,  ,
, 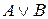 одержати
одержати  ”; (
”; ( )
)
7) “Із  ,
,  ,
,  одержати
одержати 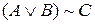 ”; (
”; ( )
)
8) “Із  ,
,  одержати
одержати  ”; (
”; ( )
)
9) “Із  , А одержати
, А одержати 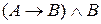 ”; (
”; (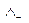 )
)
10) “Із 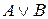 ,
, 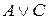 ,
,  одержати
одержати  ”; (
”; ( )
)
11) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
12) “Із  ,
,  , С одержати
, С одержати  ”; (
”; ( )
)
13) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
14) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
15) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
16) “Із  ,
,  одержати
одержати  ”; (
”; ( )
)
17) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
18) “Із  ,
,  ,
,  ,
, 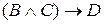 одержати
одержати  ”; (
”; ( )
)
19) “Із  ,
, 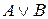 одержати
одержати  ”; (
”; (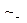 )
)
20) “Із 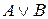 ,
,  ,
,  одержати
одержати 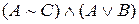 ”; (
”; ( )
)
21) “Із  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
22) “Із  ,
,  ,
,  ,
,  одержати
одержати  ”; (
”; ( )
)
23) “Із  ,
,  одержати
одержати 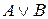 ”; (
”; ( )
)
24) “Із  ,
,  одержати
одержати  ”; (
”; (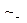 )
)
25) “Із  ,
,  одержати
одержати  ”; (
”; (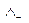 )
)
26) “Із  ,
,  ,
,  одержати
одержати  ”. (
”. ( )
)
X. Виконайте завдання.
1) Нехай  . Визначте множини істинності для кон’юнкцій поданих нижче предикатних формул: а) “
. Визначте множини істинності для кон’юнкцій поданих нижче предикатних формул: а) “  ” і “
” і “ 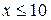 ”; б) “
”; б) “  ” і “
” і “  ”.
”.
2) Використовуючи символи кванторів, запишіть у вигляді формул подані нижче предикати: а) “Існує таке число  , що
, що  ”; б) “Для всіх
”; б) “Для всіх  , таких, що
, таких, що  , виконується нерівність
, виконується нерівність  ”.
”.
3) Дано предикати:  “ n — ціле число”,
“ n — ціле число”,  “ n — просте число”,
“ n — просте число”,  “ n — число, кратне 5”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)
“ n — число, кратне 5”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)  ; б)
; б)  ; в)
; в)  .
.
4) Предикат  задано на множині
задано на множині  матрицею виду:
матрицею виду:
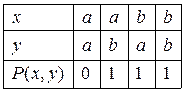
Яка з наведених нижче формул і чому визначає цей предикат: а)  ; б)
; б)  ; в)
; в)  ?
?
5) Запишіть подану нижче формулу у вигляді нормальної форми ВНФ:  .
.
6) Нехай  . Побудуйте множини істинності для кожного з поданих нижче предикатів: а)
. Побудуйте множини істинності для кожного з поданих нижче предикатів: а)  ; б)
; б) 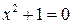 ; в)
; в)  ; г)
; г)  .
.
7) Нехай  , а також задано предикати
, а також задано предикати  “ х — просте число” і
“ х — просте число” і  “ х — раціональне число” Використовуючи квантори, запишіть у вигляді формул подані нижче твердження: а) “Будь-яке просте число є раціональним числом”; б) “Існує раціональне число, яке є простим числом”.
“ х — раціональне число” Використовуючи квантори, запишіть у вигляді формул подані нижче твердження: а) “Будь-яке просте число є раціональним числом”; б) “Існує раціональне число, яке є простим числом”.
8) У поданих нижче формулах визначте, які змінні і чому є зв’язаними, а які — вільними: а)  ; б)
; б) 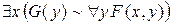 .
.
9) Нехай є комірки з номерами 1, 2, 3, 4. Використовуючи квантори, подайте у вигляді формули твердження: “Збільшити номер кожної комірки на 2”.
10) На множині парних натуральних чисел  задано два предикати
задано два предикати  “число n кратне 5”,
“число n кратне 5”,  “
“  ”. Побудуйте множини істинності для поданих нижче предикатів: а)
”. Побудуйте множини істинності для поданих нижче предикатів: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
11) Запишіть подану нижче формулу у вигляді нормальної форми ВНФ:  .
.
12) Нехай  . Побудуйте множини істинності для кожного з поданих нижче предикатів: а)
. Побудуйте множини істинності для кожного з поданих нижче предикатів: а)  ; б)
; б)  2; в)
2; в)  .
.
13) Нехай  , а також задано предикат
, а також задано предикат  “ y є функцією від х ”. Встановіть значення істинності наведених нижче формул і подайте їх звичайною мовою: а)
“ y є функцією від х ”. Встановіть значення істинності наведених нижче формул і подайте їх звичайною мовою: а)  ; б)
; б)  ; в)
; в)  .
.
14) За столом сидить шестеро осіб. Використовуючи квантори, подайте увигляді формули твердження: “Серед шести присутніх є один програміст”.
15) Предикат  задано на множині
задано на множині  матрицею виду:
матрицею виду:
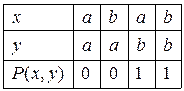
Яка з наведених нижче формул і чому визначає цей предикат: а)  ; б)
; б) 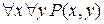 ; в)
; в)  ?
?
16) Дано предикати:  “ n — просте число”,
“ n — просте число”,  “ n — число, кратне 3”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)
“ n — число, кратне 3”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)  ; б)
; б)  ; в)
; в)  .
.
17) Вкажіть вільні й зв’язані змінні в поданих нижче формулах: а)  ; б)
; б)  .
.
18) Запишіть подану нижче формулу у вигляді нормальної форми ВНФ: 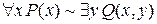 .
.
19) Нехай  . Визначте множини істинності для диз’юнкцій поданих нижче предикатів: а) “
. Визначте множини істинності для диз’юнкцій поданих нижче предикатів: а) “  ” і “
” і “  ”; б) “
”; б) “  ” і “
” і “  ”.
”.
20) На множині парних натуральних чисел  задано два предикати
задано два предикати  “число n кратне 3”,
“число n кратне 3”,  “
“  ”. Побудуйте множини істинності для поданих нижче предикатів: а)
”. Побудуйте множини істинності для поданих нижче предикатів: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
21) Визначте, чи еквівалентні подані нижче предикати: а) “  ” і “
” і “ 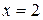 ”; б) “
”; б) “  ” і “
” і “  ”.
”.
22) Використовуючи квантори, запишіть у вигляді формули твердження: “Для того, щоб у точці  функція
функція  мала екстремум, необхідно, щоб похідна функції в цій точці дорівнювала нулю”, якщо: а)
мала екстремум, необхідно, щоб похідна функції в цій точці дорівнювала нулю”, якщо: а)  ,
,  ; б)
; б)  ,
,  .
.
23) Дано предикати:  “ n — натуральне число”,
“ n — натуральне число”,  “ n — ціле число”,
“ n — ціле число”,  “ n — просте число”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)
“ n — просте число”. Встановіть значення істинності наведених нижче формулі подайте їх звичайною мовою: а)  ; б)
; б)  ; в)
; в)  .
.
24) Дано предикати:  “ х — ціле число”,
“ х — ціле число”,  “ х — просте число”.
“ х — просте число”.  “ х — раціональне число”. Використовуючи квантори, запишіть формули для поданих нижче тверджень: а) “Будь-яке раціональне число є дробом виду
“ х — раціональне число”. Використовуючи квантори, запишіть формули для поданих нижче тверджень: а) “Будь-яке раціональне число є дробом виду  , де х — ціле число, у — натуральне число”; б) “Існують раціональні числа виду
, де х — ціле число, у — натуральне число”; б) “Існують раціональні числа виду  , де х і у — прості числа”.
, де х і у — прості числа”.
25) Нехай  ,
,  ,
,  , де І — істина, Х — хибність. При
, де І — істина, Х — хибність. При  знайдіть значення формул: а)
знайдіть значення формул: а) 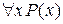 ; б)
; б)  .
.
26) На множині однозначних і двозначних парних натуральних чисел задано два предикати:  “Число х кратне 3”,
“Число х кратне 3”,  “
“  ”. Побудуйте множини істинності для поданих нижче предикатів: а)
”. Побудуйте множини істинності для поданих нижче предикатів: а)  ; б)
; б) 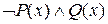 ; в)
; в)  ; г)
; г)  .
.






