Раздел 4.5 Длина волны де Бройля. Соотношение неопределённостей

 

4.5.1 Вычислить длину волны де Бройля для электрона, прошедшего ускоряющую разность потенциалов 22,5 В. (l = 258п м)

4.5.2 Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома. (D х = 124 нм)

4.5.3 Найти длину волны де Бройля для шарика массой 1 г, движущегося со скоростью 1 см/с. (l = 6,6∙10^-29 м)

4.5.4 Определить минимальную кинетическую энергию электронов в моноэнергетическом пучке, при помощи которого исследуется структура с размерами порядка 0,001 пм. (3,8∙10⁴ МэВ)

4.5.5 Найти длину де Бройля для атома водорода движущегося со средней квадратичной скоростью при температуре 300 К. (l = 145 пм)

4.5.6 Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электрон-вольтах) неопределенность энергии данного электрона. (Е = 16,7 эВ)

4.5.7 Найти длину волны де Бройля для атома водорода, движущегося при температуре 293 К с наиболее вероятной скоростью. (l = 180 пм)

4.5.8 Оценить относительную ширину спектральной линии, если известны время жизни атома в возбужденном состоянии 10^-8с и длина волны излучаемого фотона 500 нм. (D E/E = 2,65∙10^-8)

4.5.9 Найти длину де Бройля для электрона, движущегося со скоростью 10⁶ м/с. (l = 730 пм)

4.5.10 Оцените с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером 0,20 нм. (E = 1 эВ)

4.5.11 Электрон обладает кинетической энергией 0,511 МэВ. Определить длину волны де Бройля. (l = 1 пм)

4.5.12 Воспользовавшись соотношением неопределенностей, оцените размытость энергетического уровня в атоме водорода для возбужденного состояния (время его жизни 10⁸ с). (E = 414 нэВ)

4.5.13 Альфа-частица прошла ускоряющую разность потенциалов 10 кэВ. Определить для нее длину волны де Бройля. (l = 0,144 пм)

4.5.14 Покажите, используя соотношение неопределенностей, что электроны не могут входить в состав атомного ядра. Линейные размеры ядра считать равными 5∙10^{-15 м, а энергию связи нуклонов в ядре равной 10 МэВ.}

4.5.15 Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислить длину волны де Бройля для такого электрона. (l = 0,9 пм)

4.5.16 Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм. (15 МэВ)

4.5.17 Вычислить наиболее вероятную длину волны де Бройля молекул азота, содержащихся в воздухе при комнатной температуре. (l = 55,9 пм)

4.5.18 Какова должна быть минимальная кинетическая энергия электронов в моноэнергетическом пучке, используемом для исследования структуры с линейными размерами порядка 10^{-15 м. (} E = 3,8∙10⁴ МэВ)

4.5.19 Электрон обладает кинетической энергией 1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия электрона уменьшится вдвое? (увеличится в 1,12)

4.5.20 Определить относительную неопределенность D p / p импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля. (D p / p = 0,16)

4.5.21 Найти волну волны де Бройля для атома водорода, движущегося при температуре Т = 293 К с наиболее вероятной скоростью. (l = 180 пм)

4.5.22 Длина волны излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния 10^-8 с, определите отношение естественной ширины энергетического уровня, на которой был возбужден электрон, к энергии, излученного фотона. (D Е/Е = 2∙10^-7)

4.5.23 Протон обладает кинетической энергией 1 кэВ. Определить дополнительную энергию, которую необходимо ему сообщить для того, чтобы длина волны де Бройля уменьшилась в 3 раза. (D Е = 3,5 кэВ)

4.5.24 Свободно движущаяся нерелятивистская частица имеет относительную неопределенность кинетической энергии порядка 1,6∙10^-4Дж. Оцените, во сколько раз неопределенность координаты такой частицы больше ее дебройлевской длины волны. (D l/l = 12,59)

4.5.25 Вычислить длину волны де Бройля для протона, движущегося со скоростью 0,6 с, где с - скорость света в вакууме. (l = 1,76 фм)

4.5.26 Альфа-частица находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину ящика, если известно, что минимальная энергия альфа-частицы 8 МэВ. (D ℓ = 8,1∙10^-16 м)

4.5.27 Заряженная частица, ускоренная разностью потенциалов U = 200 B, имеет длину волны де Бройля 2,02 пм. Найти массу частицы, если ее заряд численно равен заряду электрона. (т = 1,67∙10^-27 кг)

4.5.28 Используя соотношение неопределенностей, оценить ширину одномерного потенциального ящика, в котором минимальная энергия электрона равна 10 эВ. (D ℓ = 6,14∙10^-11 м)

4.5.29 Альфа-частица движется по окружности радиусом 8,3 мм в однородном магнитном поле, напряженность которого 18,9 кА/м. Найти длину волны де Бройля для альфа-частицы. (l = 13,11 пм)

4.5.30 Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферической области диаметром 0,1 нм. (Е = 15 эВ)

 

Раздел 4.6 Частица в потенциальной яме

 

4.6.1 Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в средней трети ящика. (w = 0,61)

4.6.2 Частица находится в бесконечно глубокой, одномерной потенциальной яме шириной 5·10^{-10 м. Найти вид волновой функции частицы для третьего энергетического уровня и построить график зависимости плотности вероятности от координаты частицы.}

4.6.3 Частица находится в бесконечно глубокой потенциальной яме в основном состоянии. Ширина ямы L. Рассчитать вероятности нахождения частицы в интервале . Решение пояснить графически. (w = 0,48)

4.6.4 Частица находится в прямоугольной, бесконечно глубокой потенциальной яме шириной L. Вычислить отношение разности соседних энергетических уровней к энергии E_n для случаев n = 3 и n = 10. (D Е_п,3/Е₃ = 0,78; D Е_п,10/Е₁₀ = 0,21)

4.6.5 Частица находится в бесконечно глубокой, прямоугольной потенциальной яме шириной L. Построить график зависимости плотности вероятности частицы от ее координаты для возбужденного состояния (n = 3) и вычислить вероятность нахождения частицы в интервале . (w = 0,33)

4.6.6 Частица в бесконечно глубоком, прямоугольном потенциальном ящике находится на втором энергетическом уровне. Построить график зависимости плотности вероятности от координаты частицы; определить, в каких точках плотность вероятности принимает максимальные и минимальные значения. (x_max1 = L/4, x_max2 = 3L/4; x_min1 =0;x_min2= L/2; x_min3=L)

4.6.7 Частица находится в одномерной, прямоугольной, потенциальной яме шириной L. Определить, в каких точках интервала 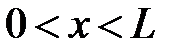плотность вероятности нахождения частицы имеет минимальное значение. Частица находится в возбужденном состоянии (n = 5). (х_min =0; L/5; 2L/5; 3L/5; 4L/5;L)

4.6.8 Электрон находится в прямоугольной потенциальной яме шириной L = 0,1 нм. Какую энергию необходимо передать электрону, чтобы перевести его из основного состояния на четвертый энергетический уровень. (Е = 560 эВ)

4.6.9 В прямоугольной, бесконечно глубокой потенциальной яме шириной L находится частица в возбужденном состоянии (n = 2). Определить вероятность нахождения частицы в интервале . (w = 0,09)

4.6.10 Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в крайней трети ящика. (w = 0,2)

4.6.11 Частица находится в бесконечно глубокой, потенциальной яме в основном состоянии. Ширина ямы L. Рассчитать вероятность нахождения частицы в интервале 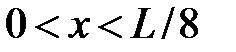. Решение пояснить графически. (w = 0,07)

4.6.12 Частица находится в бесконечно глубокой, одномерной, потенциальной яме шириной 5·10^{-10 м. Найти вид волновой функции частицы для четвёртого энергетического уровня и построить график зависимости плотности вероятности от координаты частицы.}

4.6.13 Частица находится в бесконечно глубокой, одномерной потенциальной яме шириной 1·10^{-10 м. Масса частицы m = 9,11·10-31 кг. Рассчитать энергию частицы на втором энергетическом уровне. (} E = 149,2 эВ)

4.6.14 Частица находится в прямоугольной, бесконечно глубокой, потенциальной яме на четвёртом энергетическом уровне. Ширина ямы L. Рассчитать вероятность нахождения частицы в интервале . (w = 0,25)

4.6.15 Частица массой m = 9,11·10^-31 кг находится в бесконечно глубокой, потенциальной яме шириной L = 0,1 нм. Какую энергию необходимо сообщить частице, чтобы перевести ее из основного состояния на пятый энергетический уровень. (Е = 895,2 эВ)

4.6.16 Частица находится в прямоугольной, бесконечно глубокой потенциальной яме в основном энергетическом состоянии. Ширина ямы L. Рассчитать вероятность нахождения частицы в интервале . (w = 0,7)

4.6.17 Частица находится в бесконечно глубокой, прямоугольной потенциальной яме шириной L в возбужденном состоянии (n = 4). Определить, в каких точках интервала 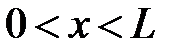плотность вероятности нахождения частицы имеет максимальное значение. (х₁ = L/8; х₂ = 3L/8; х₃ = 5L/8; х₄ = 7L/8)

4.6.18 Частица массой m = 6,64·10^-27 кг находится в прямоугольной, бесконечно глубокой потенциальной яме шириной L = 0,5 нм. Вычислить значения энергий первых трех энергетических уровней для этой частицы. (Е₁ = 1,46 эВ; Е₂ = 5,83 эВ; Е₃ = 13,14 эВ)

4.6.19 Частица находится в бесконечно глубокой, прямоугольной, потенциальной яме шириной L. Найти вид волновой функции этой частицы для основного состояния и построить график зависимости плотности вероятности от координаты частицы

4.6.20 Электрон находится в прямоугольном потенциальном ящике шириной L = 0,2 нм. Энергия электрона E = 37,8 эВ. Определить номер энергетического уровня. (п = 2)

4.6.21 Частица находится в бесконечно глубокой, одномерной потенциальной яме шириной 5·10^{-10 м. Масса частицы m = 9,11·10-31 кг. Рассчитать разность энергий между третьим и четвертым энергетическими уровнями. (}D Е₃₄ = 10,5 эВ)

4.6.22 Частица находится в прямоугольной, бесконечно глубокой потенциальной яме шириной L. Вычислить отношение разности соседних энергетических уровней к энергии E_n для случаев n = 5 и n = 7. (D Е_п,5/Е₅ = 0,44; D Е_п,7/Е₇ = 0,31)

4.6.23 Частица находится в бесконечно глубокой, прямоугольной, потенциальной яме шириной L. Рассчитать вероятность нахождения частицы в интервале координат L /3 < x < 2 L /3. Частица находится на третьем энергетическом уровне. (w = 0,33)

4.6.24 Частица находится в одномерной, прямоугольной, потенциальной яме шириной L. Определить, в каких точках интервала 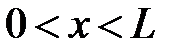плотность вероятности нахождения частицы имеет максимальное значение. Частица находится в возбужденном состоянии (n = 5). (х_max = L/10; 3L/10; 5L/10; 7L/10; 9L/10)

4.6.25 Рассчитать значения первых пяти энергетических уровней частицы массой m = 9,11·10^-31 кг, находящейся в прямоугольной, бесконечно глубокой, потенциальной яме шириной 1 нм. (Е₁ = 0,83 эВ; Е₂ = 1,51 эВ; Е₃ = 3,42 эВ; Е₄ = 6,08 эВ; Е₅ = 9,5 эВ)

4.6.26 Частица находится в одномерной, прямоугольной, потенциальной яме шириной L. Определить, в каких точках интервала 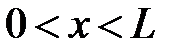плотность вероятности нахождения частицы имеет минимальное значение. Частица находится в возбужденном состоянии (n = 3). (х_min =0; L/3; 2L/3; L)

4.6.27 В одномерной прямоугольной, бесконечно глубокой, потенциальной яме шириной L находится частица. Рассчитать вероятность нахождения частицы в интервале координат . Частица находится в основном состоянии. (w = 0,82)

4.6.28 Частица находится в бесконечно глубокой, одномерной, потенциальной яме шириной 5·10^{-10 м. Найти вид волновой функции частицы для пятого энергетического уровня и построить график зависимости плотности вероятности от координаты частицы.}

4.6.29 Частица находится в бесконечно глубокой, одномерной, потенциальной яме шириной 1·10^{-10 м. Найти вид волновой функции частицы для второго энергетического уровня и построить график зависимости плотности вероятности от координаты частицы.}

4.6.30 Частица находится в бесконечно глубокой, прямоугольной потенциальной яме. Ширина ямы 10·10^{-10 м; масса частицы m = 9,11·10-31} кг. Рассчитать энергию частицы на первом и втором энергетическом уровнях. (Е₁ = 0,37 эВ; Е₂ = 1,48 эВ)

 

 

Раздел 4.7 Атом водорода

 

4.7.1 Найти наибольшую и наименьшую длину волны излучения, возникающего при переходе электрона в атоме водорода с пятого энергетического уровня в основное состояние (учесть возможность перехода через промежуточные уровни). (l_min = 94 нм; l_max = 121 нм)

4.7.2 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на пятый энергетический уровень. (Е = 0,544 эВ; l = 94 нм)

4.7.3 Спектр испускания водорода в видимом диапазоне содержит несколько спектральных линий. Какие переходы электрона в атоме водорода приводят к возникновению этих линий? Вычислить диапазон длин волн этих линий. ( нм)

4.7.4 На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны 486 нм? (D Е = 2,55 эВ)

4.7.5 Найти кинетическую энергию электрона, находящегося на k- й орбите атома водорода, для k = 1, 2, 3 и ∞. (Е₁ = 13,6 эВ; Е₂ = 3,4 эВ; Е₃ = 1,51 эВ; Е_µ = 0)

4.7.6 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на второй энергетический уровень. (Е = 10,3 эВ; l = 121 нм)

4.7.7 Найти наименьшую и наибольшую длины волн спектральных линий водорода в видимой области спектра. (l_min = 365 нм; l_max = 656 нм)

4.7.8 В каких пределах должны лежать длины волн монохроматического света, чтобы при возбуждении атома водорода квантами этого света наблюдалось три спектральных линии. (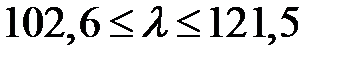 нм)

4.7.9 Какую наименьшую энергию (в электрон-вольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов спектр водорода имел три спектральных линии. Найти длину волны этих линий. (Е = 12,03 эВ; l₁ = 121 нм; l₂ = 102,6 нм; l₃ = 656,3 нм)

4.7.10 Найти наибольшую длину волны в ультрафиолетовой области спектра водорода. (l = 121 нм)

4.7.11 Вычислить энергию и длину волны фотона, испускаемого однократно ионизированным атомом гелия при переходе электрона с третьего энергетического уровня на первый. К какой области спектра относится это излучение? (Е = 12,2 эВ; l = 102 нм)

4.7.12 Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона. (Е = 2,55 эВ)

4.7.13 Определить длину волны излучения, возникающего при переходе электрона атома водорода с пятого энергетического уровня на третий. К какой области спектра относится это излучение. (l = 1278 нм)

4.7.14 Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной. (Е = 12,1 эВ)

4.7.15 Электрон в атоме водорода находится на пятом энергетическом уровне. Определить его энергию. (Ответ выразить в электрон-вольтах) Излучение с какой длиной волны возникает при переходе этого электрона в основное состояние. (Е = 0,544 эВ; l = 94 нм)

4.7.16 Фотон с энергией 15 эВ вызывает ионизацию атома водорода. Вычислить энергию образовавшегося свободного электрона и его скорость. (Е = 1,4 эВ; v = 0,7 Мм/с)

4.7.17 Вычислить длину волны фотона, если излучение обусловлено переходом с шестого энергетического уровня на основной. К какой области спектра относится это излучение? (l = 93,5 нм)

4.7.18 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода из основного состояния на четвертый энергетический уровень. (E = 12,82 эВ; l = 96 нм)

4.7.19 Вычислить длину волны фотона, если излучение обусловлено переходом электрона в атоме водорода с пятого энергетического уровня на третий. К какой области спектра относится это излучение? (l = 1278 нм)

4.7.20 Вычислить энергию электрона, находящегося на третьем энергетическом уровне в атоме водорода. Излучение, с какой длиной волны может возникнуть при переходе электронов с третьего энергетического уровня в основное состояние? (E₃ = 1,5 эВ; l = 102 нм)

4.7.21 Определить длину волны излучения, возникающего при переходе электрона в атоме водорода со второго на основной энергетический уровень. К какой области спектра относится это излучение? (l₂ = 121 нм)

4.7.22 Вычислить энергию электрона, находящегося в атоме водорода в основном состоянии и на втором энергетическом уровне. (E₀ = 13,6 эВ; E₂ = 3,4 эВ)

4.7.23 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с пятого на второй энергетический уровень. К какой области спектра относится это излучение? (l₅₂ = 432 нм)

4.7.24 Найти кинетическую энергию электрона, находящегося на k- й орбите атома водорода для k = 4,5,6 и ∞. (Е₄ = 0,85эВ; Е₅ = 0,54 эВ; Е₆ = 0,38 эВ; Е_µ = 0)

4.7.25 Найти наибольшую длину волны в инфракрасной области спектра водорода. (l =1,87мкм)

4.7.26 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с k -го на второй энергетический уровень для k = 3,4,5. К какой области спектра относится это излучение? (l₁ = 654 нм; l₂ = 484 нм; l₃ = 433 нм)

4.7.27 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с четвертого на второй энергетический уровень. К какой области спектра относится это излучение? (l₄₂ = 485 нм)

4.7.28 Рассчитать энергию и длину волны фотона, поглощение которого вызывает переход электрона в атоме водорода со второго энергетического уровня на четвёртый. (Е = 2,56эВ; l =485 нм)

4.7.29 Найти наибольшую и наименьшую длину волны излучения, возникающего при переходе электрона в атоме водорода с четвертого энергетического уровня в основное состояние (учесть возможность перехода через промежуточные уровни). (l_min =97нм; l_max = 121 нм)

4.7.30 Рассчитать длину волны фотона, испускаемого при переходе электрона в атоме водорода с третьего на второй энергетический уровень. К какой области спектра относится это излучение? (l₃₂ = 654 нм)

Раздел 4.8 Радиоактивный распад. Энергия ядерных реакций. Дефект масс

 

4.8.1 Барий-131 испытывает электронный бета-распад с периодом полураспада 11,8 суток. Ядро какого изотопа образуется в результате распада? Рассчитать активность радиоактивного источника, содержание бария-131 в котором составляет 10^-3 моль. (А = 4,09∙10¹⁴ Бк)

4.8.2 Найти энергию ядерной реакции: . (Е = 15,32 МэВ)

4.8.3 Найти массу полония ₈₄ Ро ²¹⁰, активность которого 3,7∙10¹⁰ Бк. (т = 0,22 мг)

4.8.4 Ядро тория-228 испытывает альфа-распад; постоянная распада l = 1,148·10^-4 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада тория-228 и его массу в радиоактивном источнике, если его активность 10 кБк. (Т_1/2 = 6∙10³ с; т = 3,3∙10^-17 кг)

4.8.5 Определить дефект масс и энергию связи ядра ₄ Be ⁷. (D т = 0,0382 а. е. м; Е = 35,54 МэВ)

4.8.6 Ядро актиния-228 испытывает электронный бета-распад; постоянная распада l = 31.41·10^-6 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада актиния-228 и активность радиоактивного источника, если в нем содержится 10^-6 моль актиния. (Т_1/2 = 2,21∙10⁴ с; А = 1,9∙10¹³ Бк)

4.8.7 Ядро свинца-210 испытывает электронный бета-распад; постоянная распада l = 1,077·10^-9 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада свинца-210 и его массу в радиоактивном источнике, если его активность 500 Бк. (Т_1/2 = 6,4∙10⁸ с; т = 1,6∙10^-13 кг)

4.8.8 Ядро тория-232 испытывает альфа-распад; постоянная распада l = 1,569·10^-18 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать активность радиоактивного источника, если в нем содержится 1 г радионуклида. (А = 4,1∙10³ Бк)

4.8.9 Ядро полония-210 испытывает альфа-распад; постоянная распада l = 5,797·10^-8 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада полония-210 и активность препарата, если в нем содержится 10 мг радионуклида. (Т_1/2 = 1,2∙10⁷ c; А = 1,7∙10¹² Бк)

4.8.10 Найти энергию ядерной реакции: 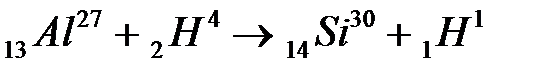. (Е = 2,4 МэВ)

4.8.11 Ядро свинца-212 испытывает электронный бета-распад; постоянная распада l = 1,906·10^-4 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада свинца-212 и его массу в радиоактивном источнике, если его активность 10 кБк. (Т_1/2 = 3,64∙10³ с; т = 1,9∙10^-17 кг)

4.8.12 Ядро радия-228 испытывает электронный бета-распад; постоянная распада l = 3.82·10^-9 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада радия-228 и его массу в радиоактивном источнике, если его активность 1000 Бк. (Т_1/2 = 1,81·10⁸ с; т = 9,92·10^-14 кг)

4.8.13 Железо-59 испытывает электронный бета-распад с периодом полураспада 45,1 суток. Ядро какого изотопа образуется в результате распада? Построить график зависимости числа дочерних ядер от времени распада железа-59 в пределах от 0 до 100 суток, если при t = 0 активность источника составляла 10 кБк.

4.8.14 Барий-131 испытывает электронный бета-распад с периодом полураспада 11,8 суток. Ядро какого изотопа образуется в результате распада? Рассчитать активность радиоактивного источника, содержание бария-131 в котором составляет 10^-3 моль. (А = 409 ТБк)

4.8.15 Натрий-22 испытывает позитронный бета-распад с периодом полураспада 2,6 года. Ядро какого изотопа образуется в результате распада? Построить график зависимости числа дочерних ядер от времени распада натрия-22 в пределах от 0 до 6 лет, если при t = 0 активность источника составляла 1 МБк.

4.8.16 Ядро урана-238 испытывает альфа-распад; постоянная распада l = 4,914·10^-18 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать массу урана-238 в радиоактивном источнике, если его активность 10⁶ Бк. (т = 81 г)

4.8.17 Вольфрам-185 испытывает электронный бета-распад с периодом полураспада 75 суток. Ядро какого изотопа образуется в результате распада? Рассчитать активность радиоактивного источника, содержание вольфрама-185 в котором составляет 10^-3 моль. (А = 6,44∙10¹³ Бк)

4.8.18 Ядро урана-234 испытывает альфа-распад; постоянная распада l = 9,002·10^-14 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать массу урана-234 в радиоактивном источнике, если его активность 10⁴ Бк. (т = 4,3∙10^-8 кг)

4.8.19 Ядро полония-214 испытывает альфа-распад; постоянная распада l = 4,226·10^-3 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада полония-214 и его массу в радиоактивном источнике, если его активность 10⁴ Бк. (Т_1/2 = 164 с; т = 8,4∙10^-19 кг)

4.8.20 Ядро тория-230 испытывает альфа-распад; постоянная распада l = 2,853·10^-13 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать массу тория-230 в радиоактивном источнике, если его активность 10³ Бк. (т = 10^-9 кг)

4.8.21 Ядро висмута-214 испытывает альфа-распад; постоянная распада l = 5,864·10^-4 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада висмута-214 и его массу в радиоактивном источнике, если его активность 400 Бк. (Т_1/2 = 1,2∙10³ с; т = 2,4∙10^-19 кг)

4.8.22 Ядро радия-226 испытывает альфа-распад; постоянная распада l = 1,371·10^-11 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать массу радия-226 в радиоактивном источнике, если его активность 10⁴ Бк. (т = 2,7∙10^-10 кг)

4.8.23 Ядро свинца-214 испытывает альфа-распад; постоянная распада l = 4,311·10^-4 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада свинца-214 и его массу в радиоактивном источнике, если его активность 500 Бк. (Т_1/2 = 1,6∙10³ с; т = 4,12∙10^-19 кг)

4.8.24 Определить дефект масс и энергию связи ядра ₄ Be ⁸. (D т = 0,0582 а. е. м; Е = 54,14 МэВ)

4.8.25 Ядро висмута-210 испытывает электронный бета-распад; постоянная распада l = 1,6·10^-6 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада висмута-210 и активность препарата, если в нем содержится 10^-4 моль радионуклида. (Т_1/2 = 4,33∙10⁵с; А = 2,02∙10^-17Бк)

4.8.26 Найти энергию ядерной реакции: 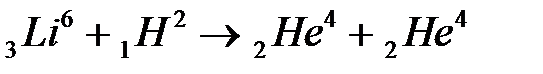. (Е = 22,4 МэВ)

4.8.27 Ядро свинца-210 испытывает электронный бета-распад; постоянная распада l = 1,077·10^-9 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада свинца-210 и его массу в радиоактивном источнике, если его активность 500 Бк. (Т_1/2 = 6,4∙10⁸ с; т = 1,6∙10^-13 кг)

4.8.28 Никель-63 испытывает электронный бета-распад с периодом полураспада 100,1 года. Изотоп какого элемента образуется в результате распада? Построить график зависимости активности радиоактивного препарата от времени распада в пределах от 0 до 300 лет, если при t = 0 активность источника составляла 1 кБк.

4.8.29 Определить дефект масс и энергию связи ядра ₅ B ¹¹. (D т = 0,082 а. е. м; Е = 76,22 МэВ)

4.8.30 Ядро радия-224 испытывает альфа-распад; постоянная распада l = 2,204·10^-6 с^-1. Ядро какого изотопа образуется в результате распада? Рассчитать период полураспада радия-224 и активность его источника, в котором содержится 10 мг радионуклида. (Т_1/2 = 3,2∙10⁵ с;А = 5,9∙10¹³ Бк)

 

 

Раздел 4.9 Задачи повышенной сложности (Волновая и квантовая оптика)

 

4.9.1 Плоскополяризованный свет, длина волны которого в вакууме l = 530 нм, падает на пластинку из кварца перпендикулярно ее оптической оси. Определите показатели преломления кварца для обыкновенного - n _о и необыкновенного - n _e лучей, если длины этих волн в кристалле соответственно равны l ₀ = 344 нм и l _е = 341 нм. (n_о = 1,54, n_e = 1,55)

4.9.2 Мыльная пленка, расположенная вертикально, образует клин. Интерференция наблюдается в отраженном свете через красное стекло (длина волны красного света 0,631 мкм). При этом расстояние между соседними красными полосами равно 3 мм. Затем эта же пленка наблюдается через синее стекло (длина волны синего света 0,470 мкм). Найти расстояние между соседними синими полосами. (ℓ₂ = 2,23 мм)

4.9.3 Плоская световая волна падает нормально на диафрагму с диаметром отверстия 6 мм. За диафрагмой на расстоянии 3 метра от нее находится экран. Какое число зон Френеля укладывается в отверстии диафрагмы? Темным или светлым будет центр дифракционной картины на экране? Длина световой волны 0,6 мкм. (N = 5)

4.9.4 В результате эффекта Комптона фотон при взаимодействии с электроном рассеялся на угол j = 90˚. Энергия рассеянного фотона равна 0,4 МэВ. Найти импульс и энергию электрона отдачи. (W = 1,94 МэВ; р_е = 9,5×10^-22 кг×м/с)

4.9.5 На стеклянный клин (n = 1,5) нормально падает монохроматический свет. Угол клина равен 4^/. Определите длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм. (l = 698 нм)

4.9.6 Найти радиусы первых четырех зон Френеля, если расстояние от источника света до волновой поверхности равно 1м, расстояние от волновой поверхности до точки наблюдения равно 1 м. Длина волны света 0,5 мкм. (r₁ = 0,71 мм; r₂ = 1 мм; r₃ = 1,22 мм; r₄ = 1,41 мм)

4.9.7 Фотон с длиной волны l = 6 пм рассеялся под прямым углом на свободном электроне. Рассчитать импульс и кинетическую энергию электрона отдачи. (W = 60 кэВ; р_е = 1,36×10^-22 кг×м/с)

4.9.8 Пучок плоскополяризованного света (l = 589 нм) падает на пластинку исландского шпата перпендикулярно к его оптической оси. Найти длины волн l _о и l _e обыкновенного и необыкновенного лучей в кристалле, если показатели преломления исландского шпата для обыкновенного и необыкновенного лучей равны n _о = 1,66 и n _e = 1,49. (l_о = 355 нм, l_e = 395 нм)

4.9.9 Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света (l = 0,6 мкм). На расстоянии а = 0,5 ℓ от источника помещена круглая непрозрачная преграда диаметром D = 1 см. Найти расстояние ℓ, если преграда закрывает только центральную зону Френеля. (ℓ = 167 м)

4.9.10 Фотон с длиной волны l = 5 пм испытал комптоновское рассеяние под углом 90^о на первоначально покоившемся свободном электроне. Найти долю энергии электрона отдачи от энергии фотона до рассеяния. (W/Е^/ = 0,33)

4.9.11 Угол между плоскостями пропускания двух одинаковых поляроидов равен 50^о. Естественный свет, проходя через такую систему, ослабляется в 8 раз. Пренебрегая потерей света на отражение, определить коэффициент поглощения света в каждом поляроиде. (k = 0,78)

4.9.12 Монохроматический свет падает на поверхность клина, пространство между поверхностями которого заполнено водой. При этом расстояние между интерференционными максимумами равно 0,3 мм. Определить расстояние между интерференционными полосами, если пространство между поверхностями будет заполнено воздухом. (d = 0,4 мм)

4.9.13 На щель шириной 0,1 мм падает нормально монохроматический свет с длиной волны l. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определите длину падающей волны, если расстояние от щели до экрана 1 м, а ширина центрального дифракционного максимума 1 см. (l = 0,5 мкм)

4.9.14 Пучок естественного света падает на систему из четырех николей, главная плоскость каждого из которых повернута на угол 60^о относительно главной плоскости предыдущего николя. Во сколько раз уменьшится интенсивность света, проходящего через систему. (в 256 раз)

4.9.15 Фотон с энергией E = 0,75 МэВ рассеялся на свободном электроне на угол j = 60˚. Определить энергию электрона отдачи. (W = 0,83 МэВ)

4.9.16 При прохождении света через трубку длиной 30 см, содержащую раствор сахара с концентрацией 10%, плоскость поляризации света повернулась на угол 13,3°. В другом растворе сахара, налитом в трубку длиной 15 см, плоскость поляризации повернулась на угол 5,2°. Определить концентрацию второго раствора. (С₂ = 7,8%)

4.9.17 Для измерения показателя преломления аммиака в одно из плеч интерферометра Майкельсона поместили откачанную трубку. При заполнении трубки аммиаком интерференционная картина для длины волны 550 нм сместилась на 300 полос. Показатель преломления аммиака n = 1,00038. Найти длину трубки. (ℓ = 22 см)

4.9.18 Определить число штрихов на 1 мм дифракционной решетки, если свет с длиной волны 600 нм нормально падает на решетку и дает первый дифракционный максимум на расстоянии 3,3 см от центрального. Расстояние от плоскости решетки до экрана, на котором наблюдается дифракционная картина, равно 110 см. (N = 50 мм^-1)

4.9.19 В результате эффекта Комптона фотон при соударении с электроном был рассеян на некоторый угол. Энергия фотона до рассеяния 1,85 МэВ, энергия рассеянного фотона 0,4 МэВ. Найти угол рассеяния фотона. (j = 90^о)

4.9.20 Интенсивность света, прошедшего через систему из нескольких призм ослабляется в 8 раз. Определить число призм в системе если известно, что главная плоскость каждой призмы повернута на угол 45^о относительно главной плоскости пропускания предыдущей призмы. (N = 3)

4.9.21 В опыте с интерферометром Майкельсона для смещения интерференционной картины потребовалось переместить зеркало на 40 мкм. Зная, что длина волны падающего излучения равна 0,470 мкм, найти на какое число полос сместилась интерференционная картина. (k = 170)

4.9.22 Кварцевую пластинку поместили между скрещенными поляроидами. Минимальная толщина пластинки вещества, при которой поле зрения анализатора максимально просветлено, равна 12 мм. Определить постоянную вращения вещества. (a = 7,5 град/мм)

4.9.23 Определить угол, на который был рассеян фотон с энергией 1,5 МэВ, при эффекте Комптона, если кинетическая энергия отдачи электрона 0,1 МэВ. (j = 12,4^о)

4.9.24 В просветленной оптике для устранения отражения света на поверхность линзы наносится тонкая пленка вещества с коэффициентом преломления 1,26 (меньшим, чем у стекла). При какой наименьшей толщине пленки отражения света от линзы не будет? Длина волны падающего света 0,55 мкм, угол падения 30°. (d_min = 0,12 мкм)

4.9.25 Во сколько раз отличаются радиусы третьей зоны Френеля для длины волны l ₁ = 400 нм и восьмой зоны для длины волны l ₂ = 600 нм. Расстояние от волновой поверхности до точки наблюдения одинаково для данных длин волн. (в 2 раза)

4.9.26 Два николя ослабляют проходящий через них пучок света в 12 раз. Определить угол между плоскостями пропускания призм, если известно, что коэффициент поглощения равен 0,8. Потерей света при отражении пренебречь. (a = 30⁰)

4.9.27 Врезультате эффекта Комптона фотон с энергией 1,02 МэВ был рассеян на свободном электроне на угол j = 150^о. Определить энергию и импульс электрона отдачи. (W =1 32, МэВ; р = 6,5×10^-22 кг×м/с)

4.9.28 Кристаллическая пластинка из исландского шпата с наименьшей толщиной d = 0,86 мкм служит пластинкой в четверть волны для l = 0,59 мкм. Определите разность ∆ n показателей преломления обыкновенного и необыкновенного лучей. (∆ n = 0,171)

4.9.29 Угол рассеяния рентгеновских лучей с длиной волны 2 пм равен 60^о, а электроны отдачи движутся под углом 30^о к направлению падающих лучей. Найти импульс квантов рассеянных лучей и импульс электронов отдачи. (р₂ = 1,66×10^-22 кг×м/с, р_е = 2×86^-22 кг×м/с)

4.9.30 На стеклянную пластинку (показатель преломления 1,5) нанесена прозрачная пленка с показателем преломления 1,4. На пленку под углом 30° падает монохроматический свет с длиной волны 0,6 мкм. Какова наименьшая толщина пленки, если в результате интерференции отраженный свет максимально ослаблен? (d_min = 115 нм)

 

 

Раздел 4.10 Физика элементарных частиц

 

4.10.1 Энергия быстрых мезонов в космических лучах равна приблизительно 3 ГэВ; энергия покоя мезона 100 МэВ. Какое расстояние в атмосфере сможет пройти мезон за время его жизни по лабораторным часам. Собственное время жизни мезона 2·10^-6с. (ℓ = 18 км)

4.10.2 Заряженная частица влетает в однородное магнитное поле, индукция которого равна 0,5 Тл, и движется по окружности радиусом 10 см. Скорость частицы равна 2,4·10⁶м/с. Найти для этой частицы отношение ее заряда к массе. (е/т = 4,8·10⁷Кл/кг)

4.10.3 Найти пороговую энергию антинейтрино в реакции . (Е = 1,8 МэВ)

4.10.4 Покоившаяся нейтральная частица распалась на протон с кинетической энергией 5,3 МэВ и p ^--мезон. Найти массу этой частицы. Как она называется. (т = 12 нг;)

4.10.5 Неподвижный нейтральный p -мезон, распадаясь, превращается в два одинаковых фотона. Найти энергию каждого фотона. Масса покоя p -мезона m = 264,2 m ₀, где m ₀ – масса покоя электрона. (Е = 67,5 МэВ)

4.10.6 Найти пороговою энергию g -кванта, необходимую для образования пары мезонов p ^-- p ⁺ в поле покоящегося протона. (Е = 320 МэВ)

4.10.7 Протоны с кинетической энергией налетают на неподвижную водородную мишень. Найти пороговое значение энергии для реакции 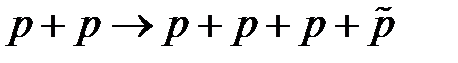. (Е = 5,6 ГэВ)

4.10.8 Выполняется ли закон сохранения лептонного заряда в реакции распада ? (выполняется)

4.10.9 Позитрон и электрон соединяются, образуя два фотона. Найти энергию каждого из возникших фотонов, если считать, что кинетическая энергия электрона и позитрона до их столкновения была ничтожно мала. (Е = 0,51 МэВ)

4.10.10 Выполняется ли закон сохранения лептонного заряда в реакции 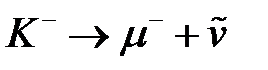? (выполняется)

4.10.11 Протоны с кинетической энергией налетают на неподвижную водородную мишень. Найти пороговое значение энергии в реакции . (Е = 0,28 ГэВ)

4.10.12 Найти пороговою энергию g -кванта, необходимую для образования пары электрон-позитрон в поле покоящегося электрона. (Е = 2,04 МэВ)

4.10.13 Найти в лабораторной системе отчета среднее время жизни мюонов, образующихся при распаде остановившихся К-мезонов по схеме 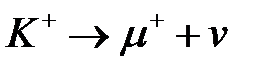. (t = 5,4 мкс)

4.10.14 Найти средний путь, проходимый p -мезоном с кинетической энергией, которая в h = 1,2 раза превышает их энергию покоя. Среднее время жизни очень медленных p -мезонов ф ₀ = 25,5 нс. (ℓ = 15 м)

4.10.15 Протоны с кинетической энергией 4 ГэВ возбуждают реакцию . Считая мишень неподвижной, найти, какое наибольшее число N p -мезонов может возникнуть в результате реакции. (N = 10)

4.10.16 Остановившийся p ⁺-мезон распался на мюон и нейтрино. Найти кинетическую энергию мюона и энергию нейтрино. (Е_m = 4,1 МэВ; Е = 29,8 МэВ)

4.10.17 Позитрон и электрон соединяются, образуя два фотона. Найти длину волны этих фотонов. (l = 2,4 пм)

4.10.18 Отрицательные p -мезоны с кинетической энергией 100 МэВ пролетают от места рождения до распада в среднем расстояние 11 м. Найти собственное время жизни этих мезонов. (t₀ = 26 нс)

4.10.19 Вычислить кинетические энергии протонов, импульсы которых равны 0,1; 1 и 10 ГэВ/с, где с – скорость света. (Е₁ = 0,05 ГэВ; Е₂ = 0,4 ГэВ, Е₃ = 9 ГэВ)

4.10.20 Остановившийся положительный мюон распался на два позитрона и два нейтрино. Найти максимально возможную кинетическую энергию позитрона. (Е = 52,5 МэВ)

4.10.21 Выполняется ли закон сохранения лептонного заряда в реакции 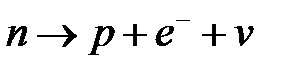?(не выполняется)

4.10.22 Известно, что распад нейтрального короткоживущего каона происходит по схеме . Принимая, что до момента распада каон покоился и его масса покоя составляет 974 m_e, определить массу покоя образовавшихся заряженных π – мезонов, если известно, что масса каждого образовавшегося пиона в 1,783 раза больше его массы покоя. (273,1 m_e)

4.10.23 Электрон и позитрон образуются фотоном с энергией 2,62 МэВ. Какова была в момент возникновения полная кинетическая энергия позитрона и электрона? (1,6 МэВ)

4.10.24 Электрон и позитрон, образованные фотоном с энергией 5,7 МэВ, дают в камере Вильсона, помещенной в магнитное поле, траектории с радиусом кривизны 3 см. Найти магнитную индукцию поля. (0,31 Тл)

4.10.25 Выполняется ли закон сохранения лептонного заряда в реакции ? (не выполняется)

4.10.26 π ⁰ – мезон распадается в состоянии покоя на два γ – кванта. Принимая массу покоя пиона равной 264,1 m_e, определите энергию каждого из возникших γ – квантов. (67,7 МэВ)

4.10.27 Позитрон и электрон соединяются, образуя два фотона. Найти энергию каждого из фотонов, считая, что начальная энергия частиц ничтожно мала. Какова длина волны этих фотонов? (0,51МэВ, 2,42×10^-12 м)

4.10.28 Выполняется ли закон сохранения лептонного заряда в реакции 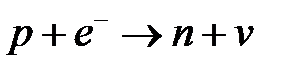? (выполняется)

4.10.29 Мезон космических лучей имеет энергию 3ГэВ. Энергия покоя мезона 100МэВ. Какое расстояние в атмосфере сможет пройти мезон за время его жизни по лабораторным часам? Собственное время жизни мезона 2 мкс. (18 км)

4.10.30 Выполняется ли закон сохранения лептонного заряда в реакции ? (не выполняется)

 

Список рекомендуемой литературы

 

1. Трофимова, Т.И. Курс физики: учеб. пособие для вузов. - 11-е изд., стер. / Т.И. Трофимова. – М.: Изд. центр «Академия», 2006. – 558 с.

2. Детлаф, А.А. Курс физики: учеб. пособие для студ. втузов. - 6-е изд., стер. / А.А. Детлаф, Б.М. Яворский. - М.: Изд. центр «Академия», 2007. – 719 с.

3. Яворский, Б.М. Справочник по физике / Б. М. Яворский, А. А. Детлаф. – 3-е изд., испр. – М.: Наука, 1990. – 624 с.

4. Волькенштейн, В.С. Сборник задач по общему курсу физики: для втузов / В. С. Волькенштейн. – 3-е изд., испр. и доп. – СПб.: Кн. мир, 2007. – 327 с.

5. Трофимова, Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов / Т. И. Трофимова, З. Г. Павлова. – 7-е изд., стер. – М.: Высш. шк., 2006. – 591 с.

 

 

Матанцева Вера Анатольевна

Плескачёва Ольга Юрьевна

Симохин Сергей Петрович

 

 

ФИЗИКА

 

Задания к расчетно-графическим работам №3 и №4