ФИЗИКА
Задания к расчетно-графическим работам №3 и №4
Для студентов инженерно-технических направлений
бакалавриата очной формы обучения,
выполняющих 4 расчетно-графические работы
БРЯНСК 2011
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Кафедра «Физика»
Утверждены научно-методическим
советом БГИТА
протокол №___ от ___________ 2011 года
ФИЗИКА
Задания к расчетно-графическим работам №3 и №4
Для студентов инженерно-технических направлений
бакалавриата очной формы обучения,
выполняющих 4 расчетно-графические работы
БРЯНСК 2011
УДК 53
Физика. Задания к расчетно-графическим работам №3 и №4 для студентов инженерно-технических направлений бакалавриата очной формы обучения, выполняющих 4 расчетно-графические работы / Брянская гос. инж.-технол. акад. Сост. В.А. Матанцева, О.Ю. Плескачева, С.П. Симохин. – Брянск: БГИТА, 2011. – 59 с.
В сборнике приведены задания к расчетно-графическим работам №3 «Электромагнетизм. Колебания и волны» и №4 «Оптика. Элементы квантовой механики. Атомная и ядерная физика». Все задания РГР разбиты на разделы, соответствующие программе по дисциплине «Физика» для студентов инженерно-технических направлений бакалавриата. Даны общие указания по выполнению расчетно-графических работ и список рекомендуемой литературы.
Для студентов очной формы обучения, выполняющих 4 расчетно-графические работы.
Рецензент
Алексеева Г.Д., доцент, канд. физ.-мат. наук
Рекомендованы редакционно-издательской и методической комиссиями
строительного факультета БГИТА
Протокол № ___ от _____________2011 года
УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
1. За время изучения курса общей физики студент должен выполнить четыре расчётно-графические работы (РГР). Количество РГР в каждом семестре определены учебным планом, сроки их выполнения устанавливаются преподавателем.
2. Номер варианта РГР задаётся преподавателем. Номера задач варианта определяются по таблице.
3. Каждая расчетно-графическая работа выполняется в отдельной тетради или на листах формата А4 (по согласованию с преподавателем). На титульном листе должны быть указаны:
1) наименование дисциплины;
2) номер и тема расчётно-графической работы;
3) номер варианта;
4) наименование факультета, специальности и номер группы;
5) фамилия, имя и отчество студента.
4. Перед выполнением задания необходимо переписать его условие (полностью, без сокращений), а затем приступать к решению. Все основные положения, приводимые при решении задач, должны сопровождаться краткими, но ёмкими пояснениями. В тех случаях, когда это возможно, следует сделать чертёж, выполненный с помощью чертёжных принадлежностей.
5. Решать задачи следует в общем виде (выразить искомую величину в буквенных обозначениях в виде рабочей формулы).
6. После получения рабочей формулы для её проверки необходимо воспользоваться правилом размерностей. Суть этого правила заключается в том, что любая формула имеет физический смысл тогда и только тогда, когда единицы измерения величин (а также отдельных слагаемых) в формуле по обе стороны от знака равенства одинаковы.
7. Числовые значения величин, выраженные в единицах СИ, подставляются в рабочую формулу и производятся вычисления.
8. Результат вычислений (ответ) записывается с использованием кратных и дольных приставок.
9. Выполненные задания РГР зачитываются в ходе устного собеседования с преподавателем.
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3
ЭЛЕКТРОМАГНЕТИЗМ. КОЛЕБАНИЯ И ВОЛНЫ
Таблица вариантов к ргр №3
| № варианта | Номер задачи | |||||||
| 3.1.1 | 3.2.1 | 3.3.1 | 3.4.1 | 3.5.1 | 3.6.1 | 3.7.1 | 3.8.1 | |
| 3.1.2 | 3.2.2 | 3.3.2 | 3.4.2 | 3.5.2 | 3.6.2 | 3.7.2 | 3.8.2 | |
| 3.1.3 | 3.2.3 | 3.3.3 | 3.4.3 | 3.5.3 | 3.6.3 | 3.7.3 | 3.8.3 | |
| 3.1.4 | 3.2.4 | 3.3.4 | 3.4.4 | 3.5.4 | 3.6.4 | 3.7.4 | 3.8.4 | |
| 3.1.5 | 3.2.5 | 3.3.5 | 3.4.5 | 3.5.5 | 3.6.5 | 3.7.5 | 3.8.5 | |
| 3.1.5 | 3.2.6 | 3.3.6 | 3.4.6 | 3.5.6 | 3.6.6 | 3.7.6 | 3.8.6 | |
| 3.1.7 | 3.2.7 | 3.3.7 | 3.4.7 | 3.5.7 | 3.6.7 | 3.7.7 | 3.8.7 | |
| 3.1.8 | 3.2.8 | 3.3.8 | 3.4.8 | 3.5.8 | 3.6.8 | 3.7.8 | 3.8.8 | |
| 3.1.9 | 3.2.9 | 3.3.9 | 3.4.9 | 3.5.9 | 3.6.9 | 3.7.9 | 3.8.9 | |
| 3.1.10 | 3.2.10 | 3.3.10 | 3.4.10 | 3.5.10 | 3.6.10 | 3.7.10 | 3.8.10 | |
| 3.1.11 | 3.2.11 | 3.3.11 | 3.4.11 | 3.5.11 | 3.6.11 | 3.7.11 | 3.8.11 | |
| 3.1.12 | 3.2.12 | 3.3.12 | 3.4.12 | 3.5.12 | 3.6.12 | 3.7.12 | 3.8.12 | |
| 3.1.13 | 3.2.13 | 3.3.13 | 3.4.13 | 3.5.13 | 3.6.13 | 3.7.13 | 3.8.13 | |
| 3.1.14 | 3.2.14 | 3.3.14 | 3.4.14 | 3.5.14 | 3.6.14 | 3.7.14 | 3.8.14 | |
| 3.1.15 | 3.2.15 | 3.3.15 | 3.4.15 | 3.5.15 | 3.6.15 | 3.7.15 | 3.8.15 | |
| 3.1.16 | 3.2.16 | 3.3.16 | 3.4.16 | 3.5.16 | 3.6.16 | 3.7.16 | 3.8.16 | |
| 3.1.17 | 3.2.17 | 3.3.17 | 3.4.17 | 3.5.17 | 3.6.17 | 3.7.17 | 3.8.17 | |
| 3.1.18 | 3.2.18 | 3.3.18 | 3.4.18 | 3.5.18 | 3.6.18 | 3.7.18 | 3.8.18 | |
| 3.1.19 | 3.2.19 | 3.3.19 | 3.4.19 | 3.5.19 | 3.6.19 | 3.7.19 | 3.8.19 | |
| 3.1.20 | 3.2.20 | 3.3.20 | 3.4.20 | 3.5.20 | 3.6.20 | 3.7.20 | 3.8.20 | |
| 3.1.21 | 3.2.21 | 3.3.21 | 3.4.21 | 3.5.21 | 3.6.21 | 3.7.21 | 3.8.21 | |
| 3.1.22 | 3.2.22 | 3.3.22 | 3.4.22 | 3.5.22 | 3.6.22 | 3.7.22 | 3.8.22 | |
| 3.1.23 | 3.2.23 | 3.3.23 | 3.4.23 | 3.5.23 | 3.6.23 | 3.7.23 | 3.8.23 | |
| 3.1.24 | 3.2.24 | 3.3.24 | 3.4.24 | 3.5.24 | 3.6.24 | 3.7.24 | 3.8.24 | |
| 3.1.25 | 3.2.25 | 3.3.25 | 3.4.25 | 3.5.25 | 3.6.25 | 3.7.25 | 3.8.25 | |
| 3.1.26 | 3.2.26 | 3.3.26 | 3.4.26 | 3.5.26 | 3.6.26 | 3.7.26 | 3.8.26 | |
| 3.1.27 | 3.2.27 | 3.3.27 | 3.4.27 | 3.5.27 | 3.6.27 | 3.7.27 | 3.8.27 | |
| 3.1.28 | 3.2.28 | 3.3.28 | 3.4.28 | 3.5.28 | 3.6.28 | 3.7.28 | 3.8.28 | |
| 3.1.29 | 3.2.29 | 3.3.29 | 3.4.29 | 3.5.29 | 3.6.29 | 3.7.29 | 3.8.29 | |
| 3.1.30 | 3.2.30 | 3.3.30 | 3.4.30 | 3.5.30 | 3.6.30 | 3.7.30 | 3.8.30 |
Раздел 3.1 Магнитное поле проводников с током.
Принцип суперпозиции полей. Закон полного тока.
3.1.1 По двум бесконечно длинным прямым проводникам, параллельным друг другу, текут токи I 1 = 10 А и I 2 = 20 А в одинаковом направлении. Кратчайшее расстояние между проводниками r = 0,1 м. Определить напряженность и индукцию магнитного поля в точке, находящейся посередине между проводниками. (НА = 31,85 А/м, ВА = 40 мкТл)
3.1.2 Токи I 1 = 0,3 A и I 2 = 0,4 А протекают по круговым виткам с радиусами R 1 = 0,1 м и R 2 = 0,1 м. Витки расположены перпендикулярно друг другу и имеют общий центр. Определить напряженность и индукцию магнитного поля в общем центре витков. (Н = 2,5 А/м, В = 3,14 мкТл)
3.1.3 По соленоиду, изготовленному из проводника диаметром d = 3 мм, протекает ток, создающий магнитное поле индукцией B = 6,3 мТл Определить силу тока, протекающего по плотно уложенным виткам соленоида. (I = 15A).
3.1.4 Токи силой I 1 = 10 A и I 2 = 2 I 1 текут по бесконечно длинным прямым параллельным проводникам в противоположных направлениях. Расстояние между проводниками r = 10 см. Найти напряженность и индукцию магнитного поля в точке, находящейся на расстоянии r 1 = r 2 = r от токов I 1 и I 2. (Н = 27,6 А/м, В = 34,6 мкТл)
3.1.5 Два проволочных круговых витка радиусами r 1 = 2 см и r 2 = 20 см лежат в одной плоскости. По виткам протекают токи I 1 = I 2 в одном направлении. Напряженность магнитного поля в общем центре витков равна Н = 275 А/м. Определить силу тока в проводниках и индукцию магнитного поля. (I 1 = I 2 = 10 A, B = 345 мкТл)
3.1.6 Витки длинного соленоида, изготовленного из провода диаметром d = 5 мм, плотно прилегают друг к другу. Определить напряженность и индукцию магнитного поля внутри соленоида, если по соленоиду протекает ток I = 50 А. (Н = 10 кА/м, В = 12,56 мТл)
3.1.7 Прямой проводник с током I = 12 A образует квадратную рамку со стороной а = 4 см. Определить напряженность и индукцию магнитного поля в центре рамки. (Н = 269 А/м, В = 338 мкТл)
3.1.8 По контуру в виде равностороннего треугольника протекает ток I = 9 A. Длина стороны треугольника а = 3 см. Определить напряженность и индукцию магнитного поля контура в точке пересечения высот треугольника. (Н = 430 А/м, В = 540 мкТл)
3.1.9 Проводник с током I = 2 А согнут под углом a = 600. Точка М лежит на биссектрисе угла на расстоянии d = 10 см от его вершины. Определить напряженность и индукцию магнитного поля в точке М. (Н = 11,9 А/м, В = 14,9 мкТл)
3.1.10 Два круговых проводящих контура имеют радиусы r 1 = 2 см и r 2 = 3 см. По контурам текут токи I 1 = 4 А и I 2 = 6 A. Найти напряженность и индукцию магнитного поля в общем центре контуров, если они расположены во взаимно перпендикулярных плоскостях. (Н = 141 А/м, В = 177 мкТл)
3.1.11 Токи I 1 = 20 A и I 2 = 30 A текут в противоположных направлениях по двум длинным прямым параллельным проводникам, расположенных на расстоянии r = 0,1 м друг от друга. Определить напряженность и индукцию магнитного поля в точке, находящейся между проводниками на расстоянии r 1 = r /2 от I 1 и r 2 = r /2 от I 2 (Н = 159 А/м, В = 200 мкТл).
3.1.12 Два скрещенных под прямым углом бесконечно длинных прямых проводника находятся на расстоянии r = 0,8 м друг от друга. По проводникам текут токи I 1 = 3 А и I 2 = 4 А. Определить напряженность и индукцию магнитного поля в середине прямой, соединяющей проводники. (Н = 2 А/м, В = 2,5 мкТл)
3.1.13 Токи I 1 = 5 A и I 2 = 3 А протекают в противоположных направлениях по круговым проводящим виткам, лежащим в одной плоскости. Радиусы витков соответственно равны: r 1 = 5 см, r 2 = 3 см. Определить напряженность и индукцию магнитного поля в общем центре этих витков. (Н = 0 А/м, В = 0 Тл)
3.1.14 Два прямых, бесконечно длинных проводника расположены параллельно друг другу на расстоянии r = 10 см друг от друга. По проводникам текут токи одинаковой величины в противоположных направлениях. Индукция магнитного поля, созданного этими проводниками в точке, удаленной на расстояния а = 6 см от первого и на b = 8 см от второго проводников, равна 10 мкТл. Определить силу тока в проводниках. (I1 = I2 = 2,4 A)
3.1.15 По тороиду, состоящему из 600 витков, протекает ток I = 10 A. Определить напряжённость и индукцию магнитного поля внутри тороида. Радиус средней линии тороида r = 6 см. (H = 16 кА/м, B = 20 мТл)
3.1.16 Напряженность магнитного поля, созданного двумя прямыми длинными проводниками, пересекающимися под прямым углом, в точке, удаленной на r 1 = 4 см от тока I 1 = 0,04 А и на r 2 = 3 см от тока I 2, равна нулю. Определить величину и направление тока I 2. (I2 = 0,03 А)
3.1.17 По двум, лежащим в одной плоскости, бесконечно длинным прямым проводникам, пересекающимся под прямым углом, текут токи I 1 = 0,04 А и I 2 = 0,03 А. Определить напряжённость и индукцию магнитного поля в точке М, удалённой на r 1 = 4 см от I 1 и на r 2 = 3 см от I 2. (H = 0 А/м, B = 0 Тл).
3.1.18 По двум проволочным виткам, лежащим в одной плоскости, протекают токи I 1 = I 2 = 10 A в одном направлении. Напряженность магнитного поля в общем центре витков H = 275 А/м. Определить радиус второго витка r 2, если радиус первого витка r 1 = 2 см. (r 2 = 20 см).
3.1.19 Прямой бесконечно длинный проводник с током I согнут под прямым углом. В точке, лежащей на биссектрисе угла и удаленной на расстоянии r = 15 см от его вершины, магнитное поле имеет индукцию В = 32,3 мкТл. Определить силу тока в проводнике. (I = 10 А)
3.1.20 Индукция магнитного поля в центре квадратного проводящего контура со стороной а = 10 см равна 56,5 мкТл. Определить силу тока в контуре. (I = 5 А)
3.1.21 Длина каждой стороны треугольника проводящего контура равна 9 см По контуру протекает ток I. В точке пересечения медиан треугольного контура индукция магнитного поля равна 120 мкТл. Определить силу тока в контуре. (I = 6 А)
3.1.22 Бесконечно длинный прямой проводник с током I = 30 А образует круговую петлю радиусом R = 15 см, касательную к проводу. Определить напряженность и индукцию магнитного поля в центре петли. (Н = 132 А/м, В = 166 мкТл)
3.1.23 По двум прямым проводникам, скрещенным под прямым углом, текут токи I 1 = 20 A, I 2 = 30 А. Расстояние между проводниками r = 20 см. Определить напряженность и индукцию магнитного поля в точке, находящейся между проводниками на расстоянии r 1 = 5 см от I 1. (Н = 71 А/м, В = 89 мкТл)
3.1.24 В точке, лежащей на середине прямой, соединяющей два прямых длинных скрещенных под прямым углом проводника с токами I 1 = I 2 напряженность магнитного поля равна 9 А/м. Определить силу тока в проводниках, если расстояние между ними r = 0,1 м. (I1 = I2 = 2 A)
3.1.25 Магнитное поле соленоида, изготовленного из проводника диаметром d = 5 мм, имеет инду к цию В = 6,28 мТл. Определить силу тока, протекающего по плотно уложенным виткам соленоида. (I = 25 А)
3.1.26 Сила тока, протекающего по соленоиду, I = 2,5 A. Индукция магнитного поля этого соленоида B = 1,26 мТл. Определить диаметр провода, из которого изготовлен соленоид. (d = 2,5 мм)
3.1.27 Индукция магнитного поля в точке М, созданного двумя параллельными бесконечно длинными проводниками с токами I 1 = I 2, равна 80 мкТл. Токи в проводниках текут в противоположных направлениях, расстояние между ними r = 0,1 м. Определить силу тока в проводниках, если точка М находится посередине между проводниками. (I1 = I2 = 10 А)
3.1.28 Магнитное поле в центре кругового витка радиусом r 1 = 6 см имеет такие же значения напряженности и индукции как и в центре другого витка радиусом r 2 = 2 см, по которому протекает ток 2 А. Определить силу тока в первом витке. (I1 = 6 A)
3.1.29 Два длинных прямолинейных проводника пересекаются под прямым углом и лежат в одной плоскости. По проводникам текут токи I 1 = 5 A, I 2 = 10 A. Определить напряженность и индукцию магнитного поля в точке, удаленной на расстояние а = 2 см от I 1 и b = 4 см от I 2 и лежащей в той же плоскости. (Н = 79,6 А/м, В = 0,1 мТл)
3.1.30 Одинаковые токи I 1 = I 2 = 20 A текут по двум бесконечным прямым параллельным проводникам в противоположных направлениях. Расстояние между проводниками r = 0,1 м. Определить напряженность и индукцию магнитного поля в точке, удаленной на r 1 = 0,08 м от I 1 и на r 2 = 0,06 м от I 2. (Н = 66,5 А/м, В = 83,5 мкТл)
Раздел 3.2 Действие магнитного поля на проводник с током
и движущийся заряд
3.2.1 В однородном магнитном поле с индукцией B = 20 Тл вращается протон. Определить частоту вращения протона. (n = 3 2МГц)
3.2.2 Два параллельных проводника длиной ℓ = 5 м каждый расположены на расстоянии d = 10 см друг от друга. По проводникам пропускают одинаковые токи I 1 = I 2 = 30 А. Определить силу взаимодействия F проводников. (F = 9 мН)
3.2.3 Нормальное ускорение a -частицы, движущейся в однородном магнитном поле равно ап = 2×1010 м/с2. Определить индукцию магнитного поля В, если скорость a -частицы v = 1,4 км/с. (В = 0,3 Тл)
3.2.4 Прямолинейный проводник, по которому идет ток I = 10 А, помещен в однородное магнитное поле с индукцией В = 0,3 Тл. Угол между направлением тока и вектором 
равен a = 300. С какой силой F действует магнитное поле на участок проводника длиной ℓ = 40 см? (F = 0,6 Н)
3.2.5 На заряженную частицу массой т = 9,1×10-31 кг, движущуюся по окружности радиусом R = 1 см в магнитном поле с индукцией В = 0,2 Тл действует сила F = 12,3 пН. Определить заряд частицы. (q = 1,67×10-19 Кл)
3.2.6 Два бесконечно длинных прямых проводника с токами I 1 = 5 A и I 2 = 3 A скрещены под прямым углом. Найти силу взаимодействия этих токов в точке, лежащей посередине между проводниками, если расстоянии между ними d = 5 см. (F = 0).
3.2.7 Найти угловую скорость вращения электрона по окружности в магнитном поле с индукцией В = 0,02 Тл. (w = 3,7×109 рад/с)
3.2.8 Момент импульса электрона, вращающегося в магнитном поле с индукцией B = 30 мТл, равен L = 1,25×10-25 кг×м2/с. Определить радиус окружности и угловую скорость электрона. (R = 0,5 см; w = 5,27×109 с-1).
3.2.9 Два параллельных проводника длиной ℓ = 1 м каждый находятся на расстоянии d = 1 см друг от друга и взаимодействуют с силой F = 1 мН. Определить силу тока в проводах, если I 1 = I 2. (I = 7 А)
3.2.10 Ион, несущий один элементарный заряд, влетает в однородное магнитное поле с индукцией В = 0,2 мТл перпендикулярно линиям поля и движется по окружности радиусом R = 10 см. Определить момент импульса L иона. (L = 3,2×10-25 кг×м2/с)
3.2.11 Шины генератора представляют собой две параллельных металлических полосы длиной ℓ = 2 м каждая, отстоящие друг от друга на расстоянии d = 20 см. Определить силу F взаимного отталкивания шин в случае короткого замыкания, когда по ним протекает ток I = 10 кА. (F = 0,2 кН)
3.2.12 Частица с зарядом q = 1,6×10-19 Кл движется в магнитном поле с индукцией В = 0,3 Тл по окружности радиусом R = 10 см со скоростью v = 2 ×106 м/с. Найти энергию частицы. (W = 4,8×10-14 Дж)
3.2.13 Два параллельных бесконечно длинных проводника с токами I 1 = I 2 находятся на расстоянии 2 см друг от друга и взаимодействуют с силой F = 1 мН на каждый метр их длины. Определить силу тока в проводниках. (I = 10 А)
3.2.14 Во сколько раз заряд частицы, движущейся со скоростью v = 106 м/с в магнитном поле с индукцией В = 0,3 Тл по окружности радиусом R = 4 см, больше элементарного электрического заряда? Энергия частицы W = 12 кэВ. (q/e = 2)
3.2.15 Во сколько раз изменится сила взаимодействия двух бесконечно длинных параллельных проводников с одинаковыми токами, если расстояние между ними и силу тока соответственно увеличить в два раза? (F2/F1 = 2)
3.2.16 Электрон движется в однородном магнитном поле с магнитной индукцией В = 0,5 Тл по окружности. Сколько оборотов N сделает электрон за время t = 1 c? (N = 14×109 об)
3.2.17 Протон и a -частица влетают в однородное магнитное поле перпендикулярно линиям магнитной индукции. Сравнить радиусы окружностей, которые описывают частицы, если у них одинаковые скорости. (Ra/Rp = 2)
3.2.18 По горизонтально расположенному проводнику длиной ℓ = 20 см и массой т = 4 г течет ток 10 А. Проводник находится во внешнем магнитном поле такой величины и направления, что сила тяжести уравновешивается силой Ампера. Определить индукцию и направление внешнего магнитного поля. (В = 20 мТл)
3.2.19 На проводник длиной ℓ = 10 см с током I = 12 А со стороны внешнего магнитного поля действует сила F = 1,6 мН. Определить индукцию магнитного поля, если угол между направлением тока и силовыми линиями поля a = 300. (В = 2,67 мТл)
3.2.20 Электрон движется в вакууме со скоростью v = 3×106 м/с в однородном магнитном поле с индукцией В = 0,1 Тл. Какова сила, действующая на электрон, если угол между направлением скорости и линиями магнитной индукции равен 900? (F = 0,05 пН)
3.2.21 Какова сила взаимодействия двух прямых проводников с токами I 1 = 1 A, I 2 = 10 А, скрещенных под прямым углом и отстоящих друг от друга на расстоянии d = 10 см? (F = 0)
3.2.22 Электрон, обладая скоростью v = 5×103 м/с влетает в однородное магнитное поле с индукцией В = 1 мТл перпендикулярно линиям магнитной индукции. Определить нормальное ап и тангенциальное аt ускорения электрона. (ап = 8,8×1011 м/с2, аt = 0)
3.2.23 Прямой проводник с током I = 25 A расположен во внешнем однородном магнитном поле перпендикулярно силовым линиям. Какова индукция магнитного поля, если на каждый метр проводника со стороны поля действует сила 10 мН? (В = 0,4 мТл)
3.2.24 Заряд частицы, движущейся по окружности радиусом 5 см в магнитном поле со скоростью 2×105 м/с, в два раза больше элементарного заряда. Энергия этой частицы 10 кэВ. Определить индукцию магнитного поля. (В = 1 Тл)
3.2.25 Два прямых, одинаковой длины ℓ проводника с токами I 1 = I 2 = 10 A расположены параллельно друг другу на расстоянии d = 5 см. Сила взаимодействия между ними F = 2 мН. Определить длину проводников. (ℓ = 5 м)
3.2.26 Определить полное ускорение электрона, влетевшего в магнитное поле с индукцией B = 10-6 Тл со скоростью v = 6 × 103 м/с перпендикулярно силовым линиям. (а = 1,05×109м/с2 )
3.2.27 Радиус кривизны траектории, по которой движется электрон в магнитном поле с индукцией В = 0,1 Тл, равен R = 0,5 см. Определить силу, действующую на электрон со стороны магнитного поля. (F = 1,4 пН)
3.2.28 Определить силу, действующую со стороны магнитного поля бесконечно длинного прямого проводника с током I = 3 A на протон, движущийся перпендикулярно проводнику в точке, отстоящей от проводника на расстоянии 30 см. (F = 0)
3.2.29 Протон, движущийся в однородном магнитном поле по окружности за 1 с делает N = 25×107 оборотов. Определить индукцию магнитного поля. (В = 16,4 Тл)
3.2.30 Определить силу взаимодействия между прямыми параллельными проводниками длиной 1 м, по которым в одном направлении текут токи I 1 = 1 A, I 2 = 10 A, если расстояние между проводниками d = 10см. Указать характер взаимодействия. (F = 20мкН.)
Раздел 3.3 Явление электромагнитной индукции. Самоиндукция
3.3.1 Круговой проволочный виток радиусом 4см находится в однородном магнитном поле, при этом плоскость витка составляет угол 300 с силовыми линиями поля. Сопротивление проводника 10 мОм. При выключении поля по витку протекает заряд Q = 1 мкКл. Определить индукцию поля В. (В = 40 мТл)
3.3.2 Максимальное значение ЭДС самоиндукции, возникающей в катушке, по которой протекает переменный по величине ток, равно ℰ max = 200 B. Определить индуктивность катушки, если сила тока в ней меняется по закону I = I 0sin wt, где амплитуда тока I 0 = 8 А, а циклическая частота w = 500 с-1. (L = 50 мГн)
3.3.3 В проволочном круговом витке, помещенном в неоднородное магнитное поле перпендикулярно силовым линиям, в момент времени 4 с возникает ЭДС индукции ℰu = 6,5 мВ. Определить радиус витка, если индукция магнитного поля меняется по закону 
, где В 0 = 5 мТл, а w = 5 с-1. (r = 0,3м)
3.3.4 В однородном магнитном поле с индукцией В = 0,6 Тл движется прямой проводник длиной 0,4 м под углом 300к линиям индукции, при этом на его концах возникает разность потенциалов U = 0,6B. Определить скорость движения проводника. (v = 5м/с)
3.3.5 Среднее значение ЭДС самоиндукции |< ℰ сu>|, возникающее в соленоиде длиной 0,8 м, состоящего из 800 витков диаметром 2 см, равно 12,6 мВ. Определить скорость изменения силы тока в этом соленоиде. ( D I /D t = 40 А/с)
3.3.6 Круговой проводящий виток помещен в магнитное поле перпендикулярно его силовым линиям. Индукция магнитного поля меняется по закону 
, Тл. В момент времени 9 с в витке возникает ЭДС индукции величиной 7 мВ. Определить радиус витка. (r = 0,32 м)
3.3.7 В прямоугольном проводнике длиной 15 см, движущемся со скоростью 13 м/с перпендикулярно силовым линиям однородного магнитного поля возникает ЭДС индукции величиной 0,5 В. Определить индукцию магнитного поля. (В = 0,26 Тл)
3.3.8 По соленоиду без сердечника протекает ток, равномерное возрастание которого вызывает возникновение в соленоиде ЭДС самоиндукции величиной 3,1 мВ. Определить скорость изменения тока, если длина соленоида 0,8 м, количество витков – 800, а их диаметр 2 см. (D I /D t = 10 А/с)
3.3.9 Прямоугольная рамка площадью 50 см2 в однородном магнитном поле индукцией 0,05 Тл расположена перпендикулярно силовым линиям поля. Под действием внешней силы рамка за 0,16 с делает четверть оборота вокруг оси, совпадающей с одной из сторон рамки. Определить среднее значение ЭДС индукции, возникающей в рамке. (ℰu = 1,6 мВ)
3.3.10 Вертикальный проводник длиной 1,5 м движется со скоростью 10 м/с в магнитном поле Земли перпендикулярно его горизонтальной составляющей с напряженностью Н г = 16 А/м в горизонтальном направлении. Определить напряжение U, возникающее между концами проводника. (U = 0,3 мВ)
3.3.11 Проволочная рамка площадью 50 см2 расположена в магнитном поле перпендикулярно его силовым линиям. Определить максимальное значение ЭДС индукции в рамке, если индукция магнитного поля меняется со временем по закону 
, где В 0 = 0,6 Тл. (ℰmax = 1,5 В)
3.3.12 Два круговых контура радиусами R = 20 см и r = 2 мм расположены в одной плоскости так, что центры совпадают. Определить ЭДС индукции, возникающую в малом контуре, если в большом за 2 мс увеличивают ток от 0 до 10 А. (|ℰи| = 0,2 мкВ)
3.3.13 Сила тока, протекающего по катушке с индуктивностью L = 0,05 Гн изменяется по закону 
, А. Найти максимальное значение ЭДС самоиндукции, возникающей в катушке. (|ℰси| = 200 В)
3.3.14 Прямоугольная рамка изготовлена из провода сопротивлением 0,2 Ом и имеет площадь 100 см2. Под углом 300 рамку пронизывают силовые линии магнитного поля, напряженность которого линейно возрастает с течение времени по закону 
, где k = 4,4 А/м×с. Найти силу индукционного тока, возникающего в рамке. (I = 0,14 мкА)
3.3.15 В магнитном поле напряженностью 20 А/м со скоростью 15 м/с движется прямой проводник длиной 2 м. Направление движения перпендикулярно силовым линиям поля. Найти разность потенциалов на концах проводника. (D j = ℰи| = 0,75 мВ)
3.3.16 Сила переменного тока, протекающего в цепи с индуктивностью 10 мГн зависит от времени по закону 
, где I 0 = 4 А – амплитуда силы тока. Найти значение ЭДС самоиндукции в этой цепи в момент времени t = 7 мс. (|ℰси| = 10,4 В)
3.3.17 В магнитном поле, напряженность которого линейно возрастает со временем по закону 
, А/м, находится контур площадью 200 см2, плоскость которого составляет угол 300 с направлением силовых линий поля. Определить ЭДС индукции, возникающую в контуре. (ℰи = 0,13 мкВ)
3.3.18 Соленоид без сердечника длиной 0,8 м и диаметром 2 см содержит 800 витков. По соленоиду протекает ток, величина которого за 0,1 с равномерно возрастает от 1 А до 5 А. Определить среднее значение ЭДС самоиндукции (|<ℰси>| = 12,6 мВ)
3.3.19 В магнитное поле, индукция которого изменяется по закону , где амплитуда В 0 = 5 мТл, а циклическая частота w = 5 с-1, помещен круговой проволочный виток радиусом r = 30 см так, что плоскость витка полностью пронизывается силовыми линиями поля. Определить ЭДС индукции, возникающей в витке в момент времени 4 с. (ℰи = 6,5 мВ)
3.3.20 Перпендикулярно линиям индукции однородного магнитного поля с индукцией 0,3 Тл движется проводник длиной 15 см со скоростью 10 м/с. Определить ЭДС, индуцируемую в проводнике. (|ℰи| = 0,45 В)
3.3.21 По катушке с индуктивностью 10 мГн протекает ток, изменяющийся по закону 
, где I 0 = 8 А – амплитуда силы тока, а w = 100 p - частота переменного тока. Определить максимальное значение ЭДС самоиндукции, возникающей в катушке. (ℰси max = 25 В)
3.3.22 Квадратную проволочную рамку со стороной 10 см, расположенную перпендикулярно линиям индукции магнитного поля с напряженностью 20 А/м, взяли за два расположенных по диагонали угла и растянули за 1 с так, что площадь рамки стала равна нулю. Определить ЭДС индукции, возникающую в рамке во время ее деформации.(ℰи = 25 нВ)
3.3.23 В катушке с индуктивностью 10,5 Гн за 1 с сила тока уменьшается от 25 А до 20 А. Определить ЭДС самоиндукции, возникшей в катушке. (|ℰсu| = 52,5 В)
3.3.24 Прямой проводник длиной 40 см движется в однородном магнитном поле со скоростью 5 м/с под углом 300 к линиям индукции. Разность потенциалов на концах проводника 0,6 В. Определить индукцию магнитного поля. (В = 0,6 Тл)
3.3.25 Проволочный виток радиусом 4 см и сопротивлением 0,01 Ом находится в однородном магнитном поле с индукцией 0,04 Тл. Плоскость рамки составляет угол 300 с направлением поля. Какой заряд протечет по витку, если поле выключить? (Q = 10 мКл)
3.3.26 Проводящий контур площадью 200 см2 расположен перпендикулярно силовым линиям магнитного поля, индукция которого меняется по закону 
Тл. Найти значение ЭДС индукции в контуре в конце четвертой секунды? (ℰи = 2,5 мВ)
3.3.27 При изменении силы тока в соленоиде на 50 А/с на его концах возникает ЭДС самоиндукции ℰси = 0,5 В. Какова индуктивность соленоида? (L = 10 мГн)
3.3.28 Поток магнитной индукции в проводящем контуре, содержащем 1000 витков, меняется по закону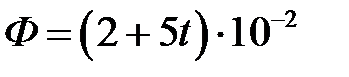 
Вб. Как зависит ЭДС индукции в контуре от времени? Какова сила тока в контуре, если сопротивление проводника 2,5 Ом? (ℰи = const, I = 20 мА)
3.3.29 Однослойный соленоид без сердечника длиной 20 см и диаметром 4 см имеет плотную намотку медным проводом диаметром 0,1 мм. За 0,1 с сила тока в соленоиде убывает от 5 А до 0. Определить ЭДС самоиндукции в соленоиде. (ℰси = 1,6 В)
3.3.30 Сила тока в соленоиде равномерно возрастает от 0 до 10 А за одну минуту, при этом соленоид накапливает энергию 20 Дж. Какая ЭДС индуцируется в соленоиде? (|ℰсu| = 67 мВ)
Раздел 3.4 Колебательные системы
(маятники, электромагнитный контур)
3.4.1 Амплитуда колебаний пружинного маятника А = 5 см, а период колебаний Т = 16 мс. Определить массу груза пружинного маятника, если максимальная энергия колебаний равна Wmax = 10 Дж. (m = 52г)
3.4.2 Период малых колебаний в вертикальной плоскости тонкого однородного стержня относительно горизонтальной оси, проходящей через конец стержня, равен T = 1,5 с. Определить длину стержня. (ℓ = 84 см)
3.4.3 Частота собственных колебаний электромагнитного контура n = 112 кГц. Определить ёмкость конденсатора, включённого в контур, если индуктивность катушки L = 4 мГн. (С = 505 пФ)
3.4.4 Диск диаметром 1м совершает малые колебания относительно оси, перпендикулярно плоскости диска и проходящей через его край. Определить время, за которое диск совершает 50 полных колебаний. (t = 50 c)
3.4.5 Период вертикальных колебаний груза массой m = 10кг равен T = 0,8 с. Определить величину деформации пружины D ℓ, возникающей под действием силы F = 9,8 Н. (Dℓ = 1,6 см)
3.4.6 На какой диапазон длин волн можно настроить колебательный контур с индуктивностью 1 мГн, если изменять емкость конденсатора от 50 до 500 пФ? (l = 421 - 1332 м)
3.4.7 Амплитуда колебаний груза на пружине 4 см, период колебаний 0,2 с, максимальная энергия 4 Дж. Определить массу груза и жесткость пружины. (т =5,1 кг, k = 5 кН/м)
3.4.8 Колебательный контур содержит конденсатор емкостью С = 80 пФ и катушку с индуктивностью L = 10-7 Гн. Найти частоту электромагнитных колебаний в этом контуре. (v = 56 МГц)
3.4.9 Входной контур радиоприемника состоит из катушки с индуктивностью L = 2 мГн и плоского конденсатора, площадь пластин которого S = 15 см2, расстояние между ними d = 2 мм, а диэлектрическая проницаемость среды e = 7,5. На какую частоту v настроен приемник? (v = 505 кГц)
3.4.10 Электрическая емкость конденсатора в электромагнитном контуре С = 2 мкФ. Период колебаний Т = 1 мс. Определить индуктивность L катушки этого контура (L = 13 мГн)
3.4.11 Во сколько раз изменится период электромагнитных колебаний в контуре, если к конденсатору контура параллельно подсоединить еще один конденсатор, емкость которого в 8 раз больше? (Т2/Т1 = 3)
3.4.12 В колебательном контуре без активного сопротивления индуктивность катушки увеличили в 8 раз, емкость конденсатора уменьшили в 2 раза. Как изменилась частота электромагнитных колебаний контура? (уменьшилась в 2 раза)
3.4.13 За какое время t в колебательном контуре с индуктивностью L = 1 мГн и емкостью С = 9 мкФ совершается N = 7×104 колебаний? (t = 42 с)
3.4.14 Стеклянный и деревянный шары, подвешенные на одинаковых пружинах, совершают свободные колебания в вертикальной плоскости. Определить отношение периодов колебаний этих шаров (Тст/Тд), если радиус первого в 4 раза меньше второго. Плотность стекла rст = 2,4 г/см3, дерева - rд = 0,6 г/см3. (Тст/Тд = 0,25)
3.4.15 Период колебаний пружинного маятника массой 10 кг Т = 0,8 с. Определить максимальную кинетическую энергию маятника, если максимальная деформация пружины равна 4 см. (Wкин = 0,5 Дж)
3.4.16 Тонкий однородный стержень длиной 80 см совершает малые колебания около горизонтальной оси, проходящей перпендикулярно стержню на расстоянии ℓ /4 от верхнего конца. Определить период и частоту свободных колебаний стержня. (Т = 1,4 с, v = 730 мГц)
3.4.17 Однородный диск радиусом R = 6,5 см колеблется вокруг горизонтальной оси, проходящей через край плоскости. Определить частоту свободных колебаний диска. (v = 1,6 Гц)
3.4.18 Колебательный контур состоит из катушки с индуктивностью L = 200 мкГн и двух соединенных последовательно одинаковых конденсаторов с емкостью С = 4 мкФ каждый. Определить частоту свободных колебаний в контуре. (v = 8 кГц)
3.4.19 Два математических маятника, длины которых отличаются на D ℓ = 16 см, за одно и тоже время совершают N 1 = 10 и N 2 = 6 колебаний. Найти длины маятников ℓ 1 и ℓ 2. (ℓ1 = 9 см, ℓ2 = 25 см)
3.4.20 Максимальная кинетическая энергия пружинного маятника Wкин = 2 Дж. Амплитуда колебаний А = 0,04 м. Найти коэффициент жесткости пружины. (k = 2,5 кН/м)
3.4.21 Период колебаний математического маятника длиной ℓ = 0,4 м в два раза больше периода колебаний пружинного маятника массой т = 0,6 кг. Определить жесткость k пружины. (k = 59 Н/м)
3.4.22 Частоты колебаний двух математических маятников отличаются в три раза. Во сколько раз отличаются длины этих маятников? (в 9 раз)
3.4.23 К спиральной пружине подвесили грузик, в результате чего пружина растянулась на 9 см. Каков будет период колебаний грузика, если его немного оттянуть вниз и затем отпустить? (Т = 0,6 с)
3.4.24 Однородный тонкий стержень длиной ℓ = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через верхний конец стержня. Найти частоту колебаний стержня. (v = 862 мГц)
3.4.25 Грузик массой т = 1000 г, подвешенный на пружине, колеблется в вертикальном направлении с периодом Т = 2 с. Определить жесткость пружины. (k = 9,87 Н/м)
3.4.26 Колебательный контур состоит из конденсатора емкостью С = 505 пФ и катушки с индуктивностью L = 4 мГн. На какую длину волны настроен этот контур? (l = 2664 м)
3.4.27 Обруч диаметром 100 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти число полных колебаний обруча N за 1 мин. (N = 42)
3.4.28 Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине вместо медного шарика подвесить алюминиевый такого же радиуса? (Т1/Т2 = 1,8)
3.4.29 К пружине подвешен груз массой т = 10 кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на ℓ = 1,5 см, найти период Т вертикальных колебаний груза. (Т = 0,78 с)
3.4.30 Однородный диск радиусом R = 0,5 м совершает малые колебания относительно оси, перпендикулярной плоскости диска и отстоящей от центра диска на 2/3 R. Найти частоту колебаний диска (v = 0,8 Гц)
Раздел 3.5 Метод векторных диаграмм
3.5.1 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.2 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.3 Методом векторных диаграмм сложить два колебания одного направления: 
и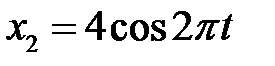 
. Записать уравнение результирующего колебания. (
)
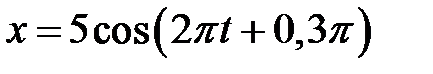3.5.4 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.5 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.6 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.7 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.8 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.9 Методом векторных диаграмм сложить два колебания одного направления: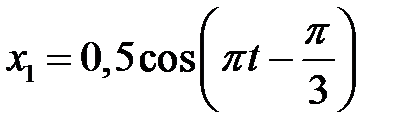 
и 
. Записать уравнение результирующего колебания. (
)
3.5.10 Методом векторных диаграмм сложить два колебания одного направления: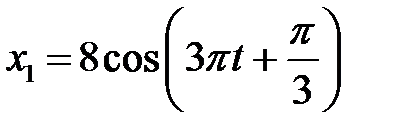 
и 
. Записать уравнение результирующего колебания. (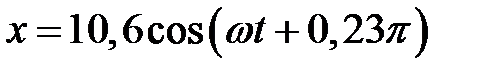
)
3.5.11 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.12 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.13 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.14 Методом векторных диаграмм сложить два колебания одного направления: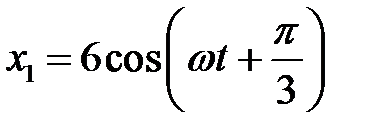 
и 
. Записать уравнение результирующего колебания. (
)
3.5.15 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.16 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.17 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (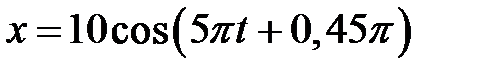
)
3.5.18 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.19 Методом векторных диаграмм сложить два колебания одного направления: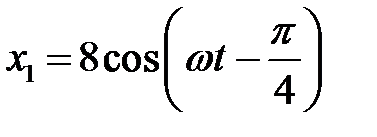 
и 
. Записать уравнение результирующего колебания. (
)
3.5.20 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.21 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.22 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.23 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.24 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.25 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (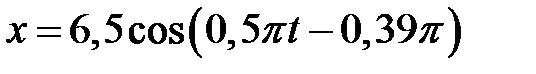
)
3.5.26 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (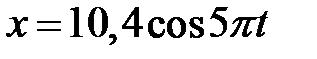
)
3.5.27 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.28 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
3.5.29 Методом векторных диаграмм сложить два колебания одного направления: 
и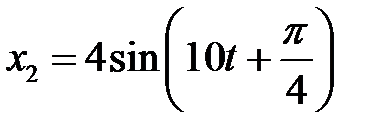 
. Записать уравнение результирующего колебания. (
)
3.5.30 Методом векторных диаграмм сложить два колебания одного направления: 
и 
. Записать уравнение результирующего колебания. (
)
Раздел 3.6 Гармонические колебания и волны
3.6.1 Точка М совершает гармонические колебания по закону 
, см и является источником плоской волны, распространяющейся по прямой. Построить график колебаний точки М. Определить амплитуду, период колебаний и смещение точки С, участвующей в волновом процессе и отстоящей на расстоянии 5 м от источника, через 10 с после начала колебаний, если скорость их распространения 2,5 м/с. (А = 3 см, Т = 2 с, хС = 0 см)
3.6.2 Идеальный колебательный контур содержит конденсатор емкостью 1 мкФ и катушку с индуктивностью 0,1 Гн. Максимальное значение силы тока в цепи контура 0,314 А. Определить частоту колебаний в контуре, максимальный заряд и максимальное напряжение на конденсаторе, если сила тока меняется по закону 
. (v = 0,5 кГц, Qmax = 0,1 мКл, Umax = 100 В)
3.6.3 Плоская волна, распространяющаяся вдоль прямой со скоростью 20 м/с. Точки М и N находятся соответственно на расстояниях 6 м и 9 м от источника и колеблются с разностью фаз D j = 3 p /4. Амплитуда колебаний 1 см. Определить длину волны, период колебаний, записать уравнения колебаний источника, точек М и N, если начальная фаза равна нулю. (l = 8 м, Т = 0,4 с)
3.6.4 Уравнение плоской электромагнитной волны, распространяющейся в вакууме, имеет вид: 
. Определить длину волны и амплитуду напряженности Н 0 магнитного поля этой волны. (l = 3 м, Н0 = 26,5 мА/м)
3.6.5 Амплитуда плоской волны, распространяющейся в упругой среде 0,003 м, частота колебаний 200 Гц, скорость распространения – 340 м/с. Записать уравнения колебаний точек, отстоящих от источника на 20 см и 60 см соответственно и определить их максимальные скорости. Найти длину волны. Начальная фаза колебаний равна нулю. (v max = 3,77 м/с, l = 1,7 м).
3.6.6 Напряжение на обкладках конденсатора в идеальном электромагнитном контуре изменяется по закону: 
, В. Емкость конденсатора 1 мкФ. Определить период колебаний в контуре. Записать закон изменения силы тока в цепи, построить график колебаний напряжения и силы тока в контуре. (Т = 2 мс, 
, А)
3.6.7 Скорость материальной точки, совершающей гармонические колебания изменяется по закону 
. Определить, в какой момент времени скорость точки максимальна. Записать уравнение колебаний точки и определить величину смещения точки в этот момент времени. Построить график колебаний точки. (t = 3 с, х(3) = 0)
3.6.8 В вакууме распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля которой 20 В/м. Найти амплитудное значение напряженности магнитного поля волны. Определить частоту электромагнитных колебаний в волне, если ее длина 440 нм. (Н0 = 53 мА/м, v = 6,8×1014 Гц)
3.6.9 Материальная точка массой 10 г совершает гармонические колебания по закону 
, м. Найти возвращающую силу в момент времени 0,1 с и полную энергию точки. Построить график колебаний этой точки в интервале времени (0 ¸ 2 Т) (Fв = -0,74 Н, Wmax = 126 мДж)
3.6.10 Электрический заряд на обкладках конденсатора в идеальном колебательном контуре изменяется по закону 
, мКл. Определить амплитуду колебаний, частоту и период колебаний, а также максимальное значение силы тока в контуре. Построить график колебаний заряда в конденсаторе и тока в цепи контура. (qmax = 0,2 мКл, v = 2 Гц, Т = 0,5 с, |Imax| = 2,5 мА)
3.6.11 Точки упругой среды, в которой распространяется волна со скоростью 1,5 м/с, колеблются с частотой 0,5 Гц по закону 
. Определить длину волны, момент времени, когда смещение
