Урок №1. Решение задач на нахождение вероятностей событий по классическому определению вероятности.

Определение 1. Равновозможными элементарными событиями будем считать такие события, любое из которых по отношению к другим событиям не обладает никаким преимуществом, т.е. не появляется чаще другого при многократных испытаниях, производимых в одинаковых условиях.

Определение 2. Вероятностью случайного события называется отношение числа равновозможных элементарных исходов, благоприятствующих этому событию, к общему числу всех равновозможных элементарных исходов, определяемого данным испытанием.

Вероятность события А равна Р(А) = .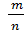

В этой формуле - число исходов испытаний, благоприятствующих событию А;

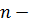число всех равновозможных несовместных исходов испытаний, образующих полную группу событий.

При вычислении вероятностей используют теорию соединений. Основными из них являются формулы для определения: 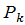- числа перестановок из k элементов:

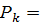k!, где k!= 1·2·3…(k-1)·k. Принято, что 0!=1.

- числа размещений из n элементов по k:

= n·(n-1)·(n-2)…(n-k+1).

Число сочетаний из n элементов по k равно

= .

Решая задачи на опыты с равновозможными элементарными исходами, нужно придерживаться общей схемы.

1.Определить, в чем состоит случайный эксперимент и, какие у него исходы. Убедиться, что они равновозможные.

2.Найти число всех возможных исходов - n.

3. Определить число исходов благоприятствующих данному событию А - m.

4. Найти вероятность события А по формуле Р(А) = .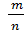

Рассмотрим задачи по теории вероятностей ЕГЭ с использованием открытого банка.

1.За­да­ние № 285922. На­уч­ная кон­фе­рен­ция про­во­дит­ся в 5 дней. Всего за­пла­ни­ро­ва­но 75 до­кла­дов — пер­вые три дня по 17 до­кла­дов, осталь­ные рас­пре­де­ле­ны по­ров­ну между чет­вер­тым и пятым днями. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции?

Ре­ше­ние. Элементарный исход- прочитан доклад профессора М.

Событие А- доклад прочитан профессором М. в последний день конференции.

За пер­вые три дня будет про­чи­тан 51 до­клад, на по­след­ние два дня пла­ни­ру­ет­ся 24 до­кла­да, всего n=51+24=75.

Благоприятных исходов – это количество докладов запланировано на по­след­ний день, т.е. m=24:2=12 до­кла­дов.

Зна­чит, ве­ро­ят­ность того, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции, равна

Р(А) =

 

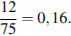
Ответ: 0,16.

2.За­да­ние № 285923. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 5 дней. Всего за­яв­ле­но 80 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны. В пер­вый день 8 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

Ре­ше­ние. Элементарный исход-порядок выступления российской команды.

Событие А-представители России выступят в третий день.

Всего выступлений n=80.

На тре­тий день за­пла­ни­ро­ва­но 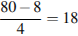вы­ступ­ле­ний-это благоприятных исходов, т.е. m= 18.

Зна­чит, ве­ро­ят­ность того, что вы­ступ­ле­ние пред­ста­ви­те­ля из Рос­сии ока­жет­ся за­пла­ни­ро­ван­ным на тре­тий день кон­кур­са, равна

 

 

Р(А) =

 

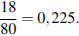
Ответ: 0,225.

3.За­да­ние № 285925. Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по бад­мин­то­ну участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 26 бад­мин­то­ни­стов, среди ко­то­рых 10 участ­ни­ков из Рос­сии, в том числе Рус­лан Орлов. Най­ди­те ве­ро­ят­ность того, что в пер­вом туре Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии?

Ре­ше­ние. Элементарный исход-Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом.

Событие А - Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из России.

В пер­вом туре Рус­лан Орлов может сыг­рать с 26 − 1 = 25 бад­мин­то­ни­ста­ми, значит всего исходов, n=25.

Благоприятные исходы - это оставшиеся участники из России m= 10 − 1 = 9. Зна­чит, ве­ро­ят­ность того, что в пер­вом туре Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии, равна

 

Р(А) =

Ответ: 0,36.

4.За­да­ние № 320170. В чем­пи­о­на­те мира участ­ву­ют 16 ко­манд. С по­мо­щью жре­бия их нужно раз­де­лить на че­ты­ре груп­пы по че­ты­ре ко­ман­ды в каж­дой. В ящике впе­ре­меш­ку лежат кар­точ­ки с но­ме­ра­ми групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Ка­пи­та­ны ко­манд тянут по одной кар­точ­ке. Ка­ко­ва ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе?

Ре­ше­ние. Элементарный исход-карточка, выбранная капитаном российской команды.

Событие А-команда России во второй группе.

Об­ще­е число кар­то­чек n =16.

Ко­ли­че­ства кар­то­чек с но­ме­ром 2 четыре, т.е. m =4.

Тем самым, вероятность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе, равна

 

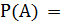
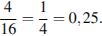
Задачу можно решить короче, если элементарным событием будет номер на карточке,тогда n =4, а m =1.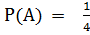

Ответ: 0,25.

5.За­да­ние № 320183. Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Физик» иг­ра­ет три матча с раз­ны­ми ко­ман­да­ми. Най­ди­те ве­ро­ят­ность того, что в этих играх «Физик» вы­иг­ра­ет жре­бий ровно два раза.

Ре­ше­ние. Событие А-в играх «Физик» вы­иг­ра­ет жре­бий ровно два раза.

Обо­зна­чим «1» ту сто­ро­ну мо­не­ты, ко­то­рая от­ве­ча­ет за вы­иг­рыш жре­бия «Фи­зи­ком», дру­гую сто­ро­ну мо­не­ты обо­зна­чим «0».

Всего исходов n= 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111.

Тогда бла­го­при­ят­ных исходов –m= 3: 110, 101, 011.

Тем самым, ис­ко­мая ве­ро­ят­ность равна:

 

Р(А) =

 

Ответ: 0,375.

6.За­да­ние № 320186. На рок-фе­сти­ва­ле вы­сту­па­ют груп­пы — по одной от каж­дой из за­яв­лен­ных стран. По­ря­док вы­ступ­ле­ния опре­де­ля­ет­ся жре­би­ем. Ка­ко­ва ве­ро­ят­ность того, что груп­па из Дании будет вы­сту­пать после груп­пы из Шве­ции и после груп­пы из Нор­ве­гии? Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние. Событие А-груп­па из Дании будет вы­сту­пать после груп­пы из Шве­ции и после груп­пы из Нор­ве­гии.

Общее ко­ли­че­ство вы­сту­па­ю­щих на фе­сти­ва­ле групп для от­ве­та на во­прос не­важ­но. Сколь­ко бы их ни было, выпишем все элементарные исходы для ука­зан­ных стран есть 6 спо­со­бов вза­им­но­го рас­по­ло­же­ния среди вы­сту­па­ю­щих (Д — Дания, Ш — Шве­ция, Н — Нор­ве­гия):

 

...Д...Ш...Н...,...Д...Н...Ш...,...Ш...Н...Д...,...Ш...Д...Н...,...Н...Д...Ш...,...Н...Ш...Д...

Всего исходов - 6, т.е. n=6.

Дания на­хо­дит­ся после Шве­ции и Нор­ве­гии в двух слу­ча­ях, m =2.

По­это­му ве­ро­ят­ность того, что груп­пы слу­чай­ным об­ра­зом будут рас­пре­де­ле­ны имен­но так, равна

 

Р(А) =

 

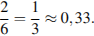
Ответ: 0,33.

За­ме­ча­ние.

Пусть тре­бу­ет­ся найти ве­ро­ят­ность того, что дат­ские му­зы­кан­ты ока­жут­ся по­след­ни­ми среди вы­сту­па­ю­щих от раз­ных го­су­дарств групп. По­ста­вим ко­ман­ду Дании на по­след­нее место и най­дем ко­ли­че­ство пе­ре­ста­но­вок без по­вто­ре­ний из преды­ду­щих групп: оно равно . Общее ко­ли­че­ство пе­ре­ста­но­вок из всех групп равно . По­это­му ис­ко­мая ве­ро­ят­ность равна

 

Р(А) =

 

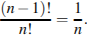
7.За­да­ние № 320190. На борту самолёта 12 мест рядом с за­пас­ны­ми вы­хо­да­ми и 18 мест за пе­ре­го­род­ка­ми, раз­де­ля­ю­щи­ми са­ло­ны. Осталь­ные места не­удоб­ны для пас­са­жи­ра вы­со­ко­го роста. Пас­са­жир В. вы­со­ко­го роста. Най­ди­те ве­ро­ят­ность того, что на ре­ги­стра­ции при слу­чай­ном вы­бо­ре места пас­са­жи­ру В. до­ста­нет­ся удоб­ное место, если всего в самолёте 300 мест.

Ре­ше­ние. Событие А- на ре­ги­стра­ции при слу­чай­ном вы­бо­ре места пас­са­жи­ру В. до­ста­нет­ся удоб­ное место.

Всего в са­мо­ле­те 300 мест, т.е. n=300.

В са­мо­ле­те 12 + 18 = 30 мест удоб­ны пас­са­жи­ру В., значит, m=30.

По­это­му ве­ро­ят­ность того, что пас­са­жи­ру В. до­ста­нет­ся удоб­ное место равна Р(А) = 30: 300 = 0,1.

 

Ответ: 0,1.

8.За­да­ние № 320191. На олим­пиа­де в вузе участ­ни­ков рас­са­жи­ва­ют по трём ауди­то­ри­ям. В пер­вых двух по 120 че­ло­век, остав­ших­ся про­во­дят в за­пас­ную ауди­то­рию в дру­гом кор­пу­се. При подсчёте вы­яс­ни­лось, что всего было 250 участ­ни­ков. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии.

Ре­ше­ние. Событие А - слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии.

Всего было 250 участников, т.е. n=250.

В за­пас­ную ауди­то­рию на­пра­ви­ли m= 250 − 120 − 120 = 10 че­ло­век.

По­это­му ве­ро­ят­ность того, что слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии, равна Р(А) = 10: 250 = 0,04.

 

Ответ: 0,04.

9.За­да­ние № 320192. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе.

Ре­ше­ние. Событие А- Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе.

Пусть один из близ­не­цов на­хо­дит­ся в не­ко­то­рой груп­пе.

Вме­сте с ним в груп­пе ока­жут­ся 12 че­ло­век из 25 остав­ших­ся од­но­класс­ни­ков,

значит n=25, а m= 12.

Ве­ро­ят­ность того, что вто­рой близ­нец ока­жет­ся среди этих 12 че­ло­век, равна Р(А) = 2: 25 = 0,48.

 

Ответ: 0,48.

Ответ: 0,48

За­да­ние № 320194. В груп­пе ту­ри­стов 30 че­ло­век. Их вер­толётом в не­сколь­ко приёмов за­бра­сы­ва­ют в труд­но­до­ступ­ный район по 6 че­ло­век за рейс. По­ря­док, в ко­то­ром вер­толёт пе­ре­во­зит ту­ри­стов, слу­ча­ен. Най­ди­те ве­ро­ят­ность того, что ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта.

Ре­ше­ние. Событие А- ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта.

Всего мест 30, n=30.

На пер­вом рейсе 6 мест, m=6.

Тогда ве­ро­ят­ность того, что ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта, равна:

 

Р(А) =

 

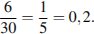
Ответ: 0,2.

11. За­да­ние № 320195. Ве­ро­ят­ность того, что новый DVD-про­иг­ры­ва­тель в те­че­ние года по­сту­пит в га­ран­тий­ный ре­монт, равна 0,045. В не­ко­то­ром го­ро­де из 1000 про­дан­ных DVD-про­иг­ры­ва­те­лей в те­че­ние года в га­ран­тий­ную ма­стер­скую по­сту­пи­ла 51 штука. На сколь­ко от­ли­ча­ет­ся ча­сто­та со­бы­тия «га­ран­тий­ный ре­монт» от его ве­ро­ят­но­сти в этом го­ро­де?

Ре­ше­ние. Событие А-ча­сто­та (от­но­си­тель­ная ча­сто­та) со­бы­тия «га­ран­тий­ный ре­монт».

Всего было продано 1000 DVD-про­иг­ры­ва­те­лей в те­че­ние года, n=1000.

В га­ран­тий­ную ма­стер­скую по­сту­пи­ла 51 штука, m=51.

Ча­сто­та (от­но­си­тель­ная ча­сто­та) со­бы­тия «га­ран­тий­ный ре­монт» равна

Р(А)= 51: 1000 = 0,051.

Она от­ли­ча­ет­ся от пред­ска­зан­ной ве­ро­ят­но­сти на 0,006, т.к. 0,051-0,045=0,006.

 

Ответ: 0,006.

12. За­да­ние № 504533. Из мно­же­ства на­ту­раль­ных чисел от 25 до 39 на­уда­чу вы­би­ра­ют одно число. Ка­ко­ва ве­ро­ят­ность того, что оно де­лит­ся на 5?

Ре­ше­ние. Событие А – число делится на 5 из множества на­ту­раль­ных чисел от 25 до 39.

Всего чисел n= 39-25+1=15.

Из 15 чисел от 25 до 39 на 5 де­лят­ся 3 числа: 25, 30 и 35, m=3.

По­это­му ис­ко­мая ве­ро­ят­ность равна Р(А)= 3: 15 = 0,2.

Ответ: 0,2.

13. За­да­ние № 504534. В случайном эксперименте бросают два игральных кубика. Найти вероятность того, что сумма выпавших очков меньше, чем 4.

Решение. Элементарный исход- упорядоченная пара чисел.

Событие А -сумма выпавших очков меньше, чем 4.

Первое число выпадает на первом кубике, а второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результатам первого броска, столбцы- второго броска. Всего исходов n=6·6=36.

 

 

Напишем в каждой клетке таблицы сумму выпавших очков и выделим клетки, где сумма выпавших очков меньше 4.Таких ячеек три. Значит, m=3. Поэтому Р(А)=3:36= .

Ответ: .

14. За­да­ние № 282854. В случайном эксперименте симметричную монету бросают дважды. Найти вероятность того, что орел выпадет ровно один раз.

Решение. Событие А- выпал ровно один орел.

Орел обозначим буквой О. Решку – буквой Р. Могут быть следующие элементарные исходы: ОО, ОР, РО, РР. Значит, n=4.

Благоприятствуют элементарные события ОР и РО, т.е. m=2.

Поэтому Р(А)=2:4=0,5.

Ответ: 0,5.

15. За­да­ние № 282856. В среднем из 1000садовых насосов, поступивших в продажу, 5 подтекают. Найти вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение. Событие А- случайно выбранный для контроля насос не подтекает. Обратим внимание на условие- из 1000 насосов 5 подтекают.

Значит, всего исходов n=1000.

А число насосов, которые не подтекают m=1000-5=995.

Поэтому Р(А)=995:1000=0,995.

Ответ: 0,995.

16. За­да­ние № 282857. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь со скрытыми дефектами. Найти вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Решение. Событие А-купленная сумка окажется качественной.

Обратим внимание на условие- на 100 качественных сумок приходится 8 со скрытыми дефектами.

Значит, всего исходов n=100+8=108.

Благоприятных исходов для данного события m=100.

Поэтому Р(А)=100:108 0,93.

Ответ: 0,93.

17. За­да­ние № 320209. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найти вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.

Решение. Событие А-часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.

В задаче идет речь о часовой стрелке, значит всего часовых делений 12, т.е. n=12.

От 10ч до 1 часа три часовых деления, значит m=3.

Поэтому Р(А)= 3:12=0,25.

Ответ: 0,25.

Задача. На 11 карточках написаны буквы я, о,р,т,е,ь,н,с,в,т,о. Каждая карточка берется в случайном порядке и прикладывается одна к другой. Найти вероятность того, что получится слово «вероятность»?

Решение. Событие А- получилось слово «вероятность».

Число всех возможных исходов- это перестановка букв с повторением

n=P (2, 2)= 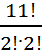=9979200

Число благоприятных исходов -m=1.

P(А)= 1\ 9979200.

Следующий тип задач с «фиксированными элементами».

Задача 2. Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1,5,9, он набрал первые четыре цифры, которые знал, и наугад комбинацию из цифр 1,5,9. Какова вероятность того, что абонент набрал верный номер?

Решение. В условии говорится, что первые 4 числа занимают вполне определенное место, т.е. «зафиксированные», а меняются местами последние три цифры.

Число всех возможных исходов – перестановки из трех элементов

Р(1,5,9) = n=3!=6

Событие А- «абонент набрал верный номер»; число благоприятных исходов m=1.

P(А)=1/6.

Ответ: 1/6.

Следующий тип-задача о выборке.

18.За­да­ние № 500998. В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах.

Ре­ше­ние.

Событие А- пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах.

6

П 4д

3

П 2д

 

Число благоприятных исходов найдем по правилу произведения исходов:

Р(А)=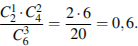

Ответ:0,6

19.За­да­ние № 325904. За круглый стол на 9стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть не рядом.

Решение. Событие А- девочки будут сидеть не рядом. Зафиксировав одну девочку, всего вариантов для второй девочки 8. Тогда 2 варианта сесть рядом с первой, тогда 8-2=6 –вариантов сесть не рядом. Вероятность того, что девочки будут сидеть не рядом Р(А)=6/8=0,75.

Ответ: 0,75.

Попробуй не реши!

Задачи с 1 по 13,16,17,25,26, 28,29,30,31,32,35,36,37,39-41,50, 53,54,58 из прототипов №5 2015г.