Дан ряд  ,
,  ,
,  . Запишите общий член ряда.
. Запишите общий член ряда.
Дан ряд с общим членом  . Un =
. Un =  . Запишите
. Запишите 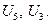 .
.
Частичная сумма ряда Sn =  .
.  , Sn =
, Sn =  ,. Определите, сходится этот ряд или расходится.
,. Определите, сходится этот ряд или расходится.
Проверьте, выполняется ли для ряда  ,
, 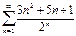 ,
,  необходимый признак сходимости?
необходимый признак сходимости?
Дан ряд 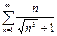 .
.  ,
,  . Чему должно быть равно
. Чему должно быть равно  , чтобы сравнить его с рядом
, чтобы сравнить его с рядом  по предельному признаку сравнения? Сходится или расходится этот ряд?
по предельному признаку сравнения? Сходится или расходится этот ряд?
Исследуйте сходимость ряда  по признаку Даламбера. (
по признаку Даламбера. ( по интегральному признаку),
по интегральному признаку),
( по радикальному признаку Коши).
по радикальному признаку Коши).
Дан знакочередующийся ряд  ,
,  ,
,  . Записать условия Лейбница для данного ряда. Составить для этого ряда соответствующий положительный ряд (*) и исследовать сходимость ряда (*).Установить характер сходимости этого ряда (абсолютная, условная или ряд расходится).
. Записать условия Лейбница для данного ряда. Составить для этого ряда соответствующий положительный ряд (*) и исследовать сходимость ряда (*).Установить характер сходимости этого ряда (абсолютная, условная или ряд расходится).
Разложите в степенной ряд функцию  ,
,  ,
, 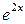 ,
,  ,
,  ,
, 
Дан ряд  .
. 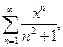

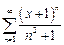 Найдите его радиус сходимости и интервал сходимости.
Найдите его радиус сходимости и интервал сходимости.
Дан ряд  . Сходится ли этот ряд при
. Сходится ли этот ряд при  ? Дан ряд
? Дан ряд  . Сходится ли этот ряд при
. Сходится ли этот ряд при  ?
?
Найдите второй член разложения функции  в ряд Тейлора в окрестностях точки
в ряд Тейлора в окрестностях точки  .
.
Найдите второй (третий) член разложения функции  ,
,  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 
( ).
).
Дана функция  . Найдите коэффициент
. Найдите коэффициент 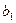 разложения её в ряд Фурье.
разложения её в ряд Фурье.
Дана функция 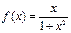 . Найдите коэффициент
. Найдите коэффициент  (запишите
(запишите  ) разложения этой функции в ряд Фурье в
) разложения этой функции в ряд Фурье в  .
.
Дана функция  . Найдите коэффициент
. Найдите коэффициент 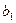 (запишите
(запишите  ) разложения этой функции в ряд Фурье в интервале
) разложения этой функции в ряд Фурье в интервале  ,
,  .
.
Экзаменационные вопросы
.«Дифференциальные уравнения (ДУ) первого порядка». Задача Коши.
Основные классы ДУ первого порядка: уравнения с раздляющ.перем., линейные однородные и неоднородные уравн.в полных дифф., уравн. Бернулли
ДУ высших порядков. Задача Коши.
ДУ, допускающие понижение порядка.
Линейные ДУ высших порядков. Линейные однородные (ЛОДУ) с постоянными коэффициентами.
Линейные неоднородные ДУ (ЛНДУ) с постоянными коэффициентами. Метод неопределенных коэффициентов
ЛНДУ. Метод вариации произвольных постоянных.
Системы ДУ. Задача Коши для норм. системы ДУ.
Решение систем ДУ методом исключения. Структура общего решения.
Кратные интегралы.
Двойной интеграл. Сведение двойного интеграла к повторному
Тройной интеграл. Вычисление тройного интеграла
Замена переменных в кратных интегралах. Переход от декартовых координат к полярным, цилиндрическим и сферическим координатам.
Приложения двойных и тройных интегралов
Числовые ряды. Осн. понятия.
Знакопол. ряды. Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Абс. и усл.сх.
Функциональные ряды, степенные ряды. Теорема Абеля. Радиус сходимости. Интервал сходимости, область сходимости. Ряды Тейлора и Маклорена. Разложение некоторых функций в ряд Маклорена
Тригонометрическая система функций. Ряд Фурье. Разложение функций в ряд Фурье.
Разложение функции в ряд Фурье на 
Ряд Фурье в произвольном промежутке.
Теорема Дирихле. Разложение функции в ряд Фурье на  .
.






