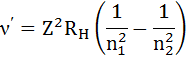Бор теориясы бойынша сутегі атомының құрылысы

Сутегі атомы жайындағы Н.Бор теориясы атомның ядролық моделіне негізделген. Бор теориясы бойынша сутегі атомы бір элементар оң зарядтан және оны айнала қозғалған бір электроннан тұрады. Сутегі атомының ядросының массасы электрон массасынан 1836 есе артық, яғни ядроны шексіз ауыр деп санауға болады.

Сонымен электрон ядроны айнала қозғалады, ал ядро айналмайды деп жорып, электрон қозғалысын қарастырайық.

Егер ядроның заряды 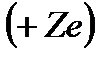, электрон заряды (-е), олардың арақашықтығы – r болса, онда Кулон заңы бойынша олардың өзара тартылыс күші:

 

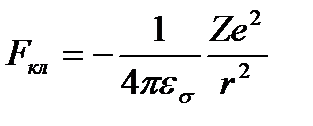(1.7.1)

 

мұндағы 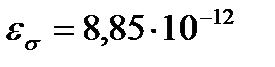Ф/м – вакуумдағы электрлік тұрақты.

Электрон ядроны айнала қозғалса, онда оған центрге тепкіш күш әсер етеді.

 

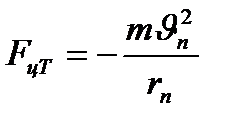(1.7.2)

 

мұндағы 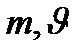және r электронның массасы, жылдамдығы және электрон қозғалған дөңгелек орбитаның радиусы, (-) минус таңбасы күштің центрге бағытталғанын көрсетеді.

Динамиканың тепе-теңдік шарты бойынша, атом орнықты болу үшін, осы екі күш бір-біріне тең болуға тиіс:

 

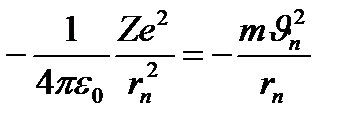бұдан 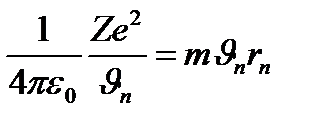(1.7.3)

 

немесе Бор постулатындағы (1.6.1) теңдік бойынша тұрақты мәнге теңестірсек

 

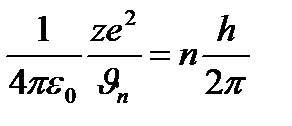(1.7.4)

бұдан

(1.7.5)

 

Бұл формула n-орбитадағы электрондардың жылдамдығын көрсетеді.

Электронның импульс моментіне жылдамдықтың мәнін қойсақ, онда n-ші орбитаның радиусын табуға болады.

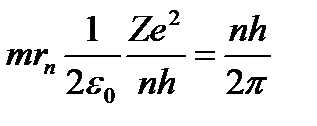бұдан 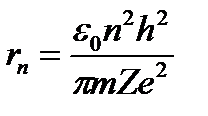(1.7.6)

 

Соңғы (1.7.5) және (1.7.6) формулалардан электрон жылдамдығы орбитаның реттік нөміріне кері пропорционал, ал радиусы орбитаның реттік нөмірінің квадратына тура пропорционал екендігін көреміз.

Сутегі атомы үшін Z=1, n=1, онда

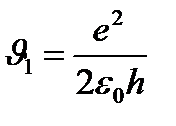(1.7.7)

ал

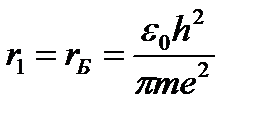(1.7.8)

 

мұндағы, 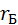-Бор орбитасының радиусы деп аталады. Соңғы (1.7.7) және (1.7.8) екі теңдікке сан мәндерін қойсақ, онда 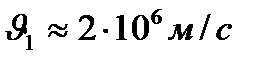, ал 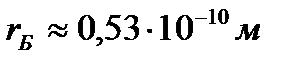болып шығады. Енді электронның стационар орбитадағы толық энергиясын анықтайық:

 

Е=Е_к+Е_р (1.7.9)

 

- жылдамдық мәнін қойсақ онда,

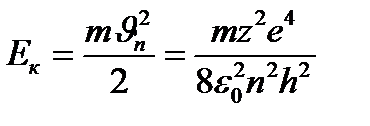(1.7.10)

 

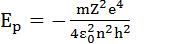(1.7.11)

 

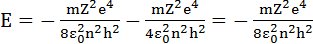(1.7.12)

 

Бұл энергияны r – радиусы арқылы өрнектесек:

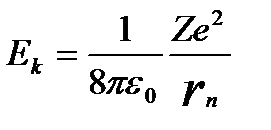(1.7.13)

 

ал 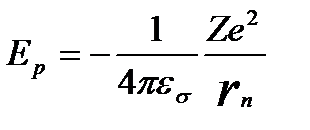(1.7.14)

 

онда, 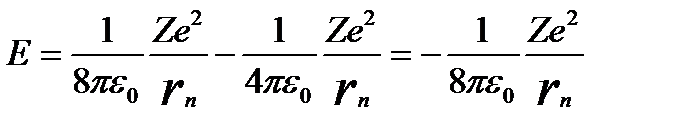(1.7.15)

 

(1.7.15) формула атом ядросы қозғалмайды деп қарастырғанға сәйкес келеді.

(1.7.12) формуланы сутегі үшін қолданып, (n=1; Z=1) сан мәндерін қойсақ, онда толық энергия

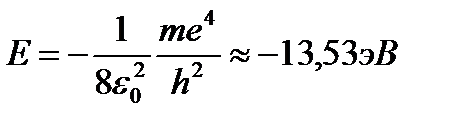
Еn3

Еn2

Еn1

Еm

 

 

Сурет

Олай болса, стационар орбитадағы электронның толық энергиясы, атомның энергетикалық деңгейі деп аталады (1.8-сурет).

Біз жоғарыда есепті жеңілдету үшін ядро қозғалмайды, оны айнала шеңбер бойымен электрон қозғалады деп есептедік. Шын мәнінде ядрода, электронда ортақ масса центрін айнала қозғалады. Дәлірек айтсақ ядроның қозғалысы да есепке алынуы керек. Бұл жағдайда жоғарыда келтірілген формулалардағы электрон массасының орнына келтірілген масса деп аталатын 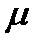шамасы алынады, ол былай анықталады:

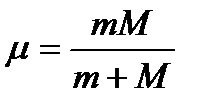(1.7.16)

 

мұндағы М – ядроның, ал m – электрон массасы. Сонда (1.7.12) теңдік бойынша стационар күйдегі электрон энергиясы былай өрнектеледі:

 

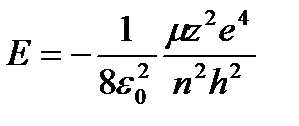(1.7.17)

 

Бұл (1.7.17) формула (1.7.12) мен (1.7.15) формулаларға қарағанда энергияны дәлірек анықтайды.

Стационар күйдегі электрон энергиясы теріс шама, сондықтан да диаграммамен кескіндегенде электрон энергиясы төменнен жоғары қарай артады. Егер негізгі күйдегі сутегі атомына сырттан 13,53эв немесе бұдан артық энергия берілсе, онда электрон атомнан бөлініп кетеді, сутегі атомы иондалады. Сонымен сутегі атомының иондалу энергиясы 13,53эв-қа тең, ал иондалу потенциалы 13,53эв болады. Егер негізгі күйдегі сутегі атомына 13,53эв-тан кем энергия берілсе, онда электрон жоғарғы энергия деңгейлерінің біріне көшеді, мысалы 10,2эв берілсе, ол бас кванттық саны n=2 деңгейіне көшеді, ал 10,2эв энергия, осы деңгейді қоздыру энергиясы болып табылады.

Егер сутегі атомының жоғарғы стационар күйдегі энергиясы Е₂, төменгі стационар күйдегі энергиясы Е₁ болса, онда атом бастапқы күйден соңғы күйге көшкенде монохраматты жарық квантын шығарады, оның тербеліс жиілігі:

 

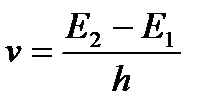(1.7.18)

(1.7.17) формуладағы энергия мәндерін (1.7.18) формулаға қойсақ, онда

 

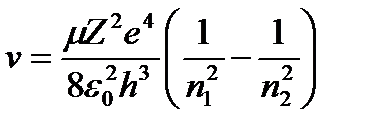(1.7.19)

 

ал толқындық сан

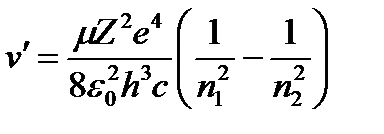(1.7.20)

 

немесе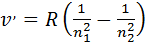

бұл формуладағы 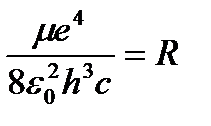, R =109678 см^-1 Ридберг тұрақтысына тең болады, сонда (1.7.20) формуласы кез келген химиялық элемент үшін мынадай түрге келеді:

 

; ;

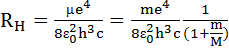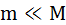онда