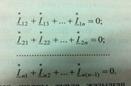Егер де R,L,С элементтер параллельді қосылған тізбекке синусойдалды кернеу
) ынта салынса, онда бұл тізбектен өткен ток параллельді тармақтардан өтетін токтардың алгебралық қосындысына тең (Кирхофтың I заңы б\ша): 
;I=Ir+Il+Ic;U=Ur+Ul+Uc;u=u*e(jᵠ)
Ом заңы бойынша тармактагы токтар Ir=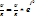 
:
Индуктивті ток: Il= 
Сыйымд. Ic= 
= 
R кедергідегі 
ток U кернеумен фаза бойынша біртектес, L индуктивтігі 
ток 
бұрышқа қалады, ал С cыйымдылықтағы 
ток π/2 бұрышқа u кернеуден озады. 
24.Синусоидалы ток тізбектеріндегі қуаттары. Тізбектің кернеуі u=UmSINwt,ал тогы i=ImSIN(wt-u).
Лезді қуат: P=ui=UmImsinwtsin(wt-u)=UI[cosu-cos(2wt-u]
Яғни екі бөліктен құралады:тұрақты шама UIcosu және кернеумен токтын жиіліктерінен екі есе үлкен сонусоидалы шамадан T уақыт ішінде екінші қосындының орташа мәні нөлге теңСондықтан тізбектегі активтік қуат
P= 
=UTcosu
Cosu-қуат коэфициент д.a Активтік қуат баска турде көрсетуге болады P=R 
=g 
= 
=U 
Кедергі және индуктивтігі бар тізбекті карап шыгайыкБұл жаіғдайда 0<u< және 0<cosu<1
u және i таңбалары бірдей кездегі уакыт аралыкта лезді куат болымды;энергия көзден қабылдағыш қа түседі де кедергіге жұтылады және индуктивтің магнит өрісінде қолданады. u және i таңбалары кері кездегі уакыт аралыкта лезді куат теріс; энергияның бір бөлігі көзге қайтадыАктивтік сыйымдылық тізбекте көрініс ұқсас болады(0>u>- ). Активті қуат.Активті қуат деп лездік қуаттың бір периодтағы орташа мағынасы: 
. Синусоидалы ток үшін активті қуат: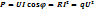 
тең. Мұндағы U,I – қолданылған кернеу мен токтың мәні, 
-кернеу мен токтың фазалар айырымы.Активті қуаттың өлшем бірлігі-Ватт (Вт).
Реактивті қуат. Реактивті қуат тепе-теңдігі: 
.Мұндағы x,b –реактивті кедергі мен өткішгіштік.Өлшем бірлігі-ВАр түрінде жазылады.
Толық қуат.Толық қуат теңдеуі:S=UI.Өлшем бірлігін-ВА(вольт-ампер).Синусоидалы ток үшін активті,реактивті және толық қуат былай байланыстырылады: 
.
Кешенді қуат.Кешенді қуат теңдеуі: 
.Мұндағы 
мына токпен түйістірілген токтың кешені.
26.Топографиялық сызба - бұл кешенді потенциялдар сызбасы. Сұлбаның әрбір нүктесі топографиялық сызбаның нүктелеріне сәйкес келеді. Потенциялы 0-ге тен нүкте, топографиялық сызбаның бас кординатасына сәйкес келеді. Топографиялық сызба қолдану арқылы нүктелер арасындағы кернеуді азайтуға болады. Топографиялық сызбадағы кернеу векторы нүктеге қатысты сәйкесінше нүктелерге оң бағытталған кернеуге қарама-қарсы бағытталған. Топографиялық сызбаны тұрғызу үшін нүктелердің кешенді потенциялдарын анықтап алып, анықталған мәндерді кешенді жазықтықта тұрғызамыз.Топографиялық сызбаны салуға мысал келтірілген:
28.Комплексті кедергілердің параллель жалғанған кездегі тізбекті есептеу: Екі параллелді тармақтары бар: біреуі кедергімен және индуктивтілікпен, екіншісі кедергімен және сыйымдылықпен тізбекті қосылған сұлбаны қарап шығайық. Мұндай тізбекті параллель тербелмелі контур деп атайды. Яғни Z1,Z2 кедерг3лер3 параллель жалғанған. Бұл кезде әрбір кедергінің кернеулері кіріс кернеуіне тең болады U=U1+U2, ал ток күші әрбір ток күштерінің қосындысы кірістегі токка тең болады. Толық ток күші I=U/Z; I1=U1/Z1; Z1= R1+jXL1; Z2=R2+jXC2; I2=U2/Z2; I=I1+I2; Z=Z1*Z2/(Z1+Z2); Векторлық диаграммада кескіндейтін болсақ кірістегі ток әрбір елементтердің токтарының қосындысына тең болып шығуы қажет.
29.Комплексті кедергілердің аралас жалғанған кездегі тізбекті есептеу: Аралас жалғану ол бірізді және паралель жалғанған кедергілердін тіркестері: Комплексті кедергілері z1,z2,z3 сәйкесінше аралас жалғанған. Жалпы кедергі z=z1+ 
.Сонда тоқ күштерін есептейміз I1=U/z; I2=I1*z3/(z2+z3); I3=I1*z2(z2+z3); Векторлық диаграммада I1=I2+I3 болып шығуы керек.
Кернеулері 
U2=I2*Z2; U3=I3*Z3; Барлық тармақтардағы кернеулердін қосындысы кірістегі кернеудін шамасына тен болады. Векторлық диаграммада U1=U2+U3 болып шығуы керек. Векторлық диаграммада токтардың бағыты сәйкесінше кернеуледің бағытымен бағыттас болып шығуы тиіс. Диаграмманы өзің сызып ал.
30.Тармақталған синусоидалы ток тізбектері үшін Кирхгоф заңдары. Дифференциалдық түр- дегі Кирхгофтың заңдары айнымалы токтар мен кернеулердің лездік мәнін жазуға көмектеседі. Кирхгофтың 1 заңы: сұлбадағы токтың лездік мәндерінің қосындысы нольге тең бт: 
=0
Кирхгофтың 2 заңы: ЭҚКнің лездік мәнінің барлық тұйықталған контурдағы кернеудің алгебралық қосындысы, сол контурдағы элементтердің кернеулерінің алгебралық қосындысына тең: 
Кешенді түрдегі Кирхгофтың заңдары кешенді амплитуда және токтың, кернеудің, ЭҚКнің кешенді мәндері үшін жазылады Кирхгофтың 1 заңы: сұлбадағы түйіндердің комплекстік токтың мәндерінің алгебралық қосындысы нөлге тең болып табылады: 
=0 I с точкой напиши и на индекс к впиши.
Кирхгофтың 2 заңы: кешенді ЭҚКнің барлық тұйықталған контурдағы кернеудің алгебралық қосындысы, сол котурдағы элементтердің кернеулерінің алгебралық қосындысына тең:
(RkIk+LKIKjw - 
Кирхгофтың заңдарын кешенді түрде анықтайтын теңдеулер
Синусоидалды ток үшін: =0 
= 
Сол сияқты тұрақты ток үшін: =0 
=
31. Контурлық тоқтар әдісімен синусоидалы ток тізбектерін есептеу. Берілген тізбекте контурлардың бойымен өтетін кешендік контурлық тоқтарды енгіземіз. олардың бағытын өз еркімізбен таңдаймыз. сол КТ қатысты теңдеу жүйесін құрып, белгісіз кешенді токтарды анықтаймыз.
(
+ 
- 
+ 
+ 
)- 
( + )= 
- ( + )+ ( + + 
- 
)= 
= + 
-
= +
= -
( + )- 
=
- 
+ ( + )=
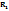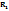Сонда тармақтағы кешенді тоқтар келесі түрде анықталады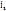 
= 
= - 
=
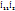32.ТПӘ мен синусоидалы тоқ тізбек-н есеп-у. Бұл әдіс Кирх 1-заңына ж/е Омның з-н қолд-ға нег-н.Күрделі тізбек-ң қайсысы болған түйін-ң потенц-н нһлгетең деп алуға б-ы.Басқа түйіндермен базистік түйін-ң ара-ғы кернеу сол түйіндер-ң потенциалы б-ы.Бұл потенц-ды тармақ-ң өткізгіш-не көбейткенде сол тармақтағы ток табыл-ы.Егерде электр тізбек-гі түйінді потенц-рды тапсақ,онда тармақ-ң ток-н таб-з. К 1-заңы б/ша 1 ж/е 2 түйін-р үшін 
Y11 
-Y21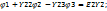 
Y=1/z;
Y11=Y1+Y3+Y4;Y12=Y21=Y3;Y13=Y4;Y23=Y5;Y22=Y2+Y3+Y5;
33.Екі түйін әдісі ТПӘ-нің жеке жағдайы болып табылады. Яғни бұндай тізбекте тек 2 түйін болуы керек. Түйіндер арасындағы кернеу комплексін есептейміз: 
Мұндағы, 
, 
Тармақтардағы тоқтар комплекстерін Ом заңы бойынша есептейміз:
40 Өзара индуктивті байланысқан элементтердің параллель жалғануы
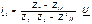
41.Синусоидалы ток тізбектері үшін қуаттар тепе-теңдігі. Энергияның сақталу заңынан шығатыны-ол кез келген тізбекте лездік және активті қуаттарының да тепе-теңдіктері сақталады.Энергия көздерінен беріліп тұрған барлық қуаттарының қосындысы,барлық қабылдағыштардағы қабылданған қуаттардың қосындысына тең.Комплекстік үшін де тепе-теңдіктің сақталатынын көрсетеді.
Сұлбаның жалпы түйіндер саны n болсын делік.Мұндағы түйін дегеніміз-ол сұлбаның кез-келген екі немесе одан да көп элементтерінің қосылған жері.Тармақ дегеніміз-сұлба элементтерінің біреуінен тұратын әрбір сұлба телімі.
Әрбір n түйін үшін Кирхгофтың бірінші заңы бойынша комплекстер үшін оған түйіндес жиынтық токтарға теңдеулер құрамыз:
