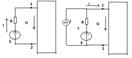
1,18а – суретте ЭҚК-тің көзінен ток көзіне ауысу сұлбалары
1,18а – суретте ЭҚК-тің көзі R ішкі кедергісімен 1 және 2 қысқыштарға жалғанған, ал қысқыштар арасындағы кернеу U.
Ток I тең
= 
- 
=J-Ii (1,42)
J= - ток көзінің тогы Ii= - ішкі кедергідегі токІ- ЭҚК-тің көзінің тогы(1.42) тендеуге 1.18,б – суреттегі эквивалентті сүлбе сәйкес келеді.Токкөзі тогы ЭҚК-тің бағытымен бір бағыттас.
E (кернеу) көзі идеалды ток көзі Rішк=0
Айқын ток көзі, Rішкі кедергі мен ток көзімен параллель жалғанған эквивалентті схемамен ғана ауыстырылады.
 |
12 Электр тізбектерінің өзаралық қасиеті Сызықты электр тізбектерінде қандай да бір m тармағындағы Em ЭҚК әрекет еткендегі к тармағындағы Ek ЭҚК әрекет еткендегі m тармағындағы токқа тең болады. Бұл кезде Ek=Em болуы керек.сонымен қатар ЭҚК ж/е токтардың бағыты бір біріне қатысты бірдей болуы керек.
14. Электр тізбегі тармақтарының кірістік және өзара өткізгіштіктері. Электр тізбегінің кез-келген тармағының кірістік өткізгіштігі сол тармақтағы токтың ЭҚК-іне қатынасымен анықталады. Кірістік өткізгіштіктің индекстері бірдей болады.(бұл кезде қалған ЭҚК-р 0-ге тең болуы керек.) 
= 
-кірістік өткігіштік Электр тізбектерінің кез-келген 2 тармағының өзара өткізгіштігі бір тармақтағы токтың екінші тармақтағы ЭҚК-іне қатынасымен анықталады. Қалған тармақтағы ЭҚК-р бұл кезде 0-ге тең болуы керек. 
-өзара өткізгіштік. = 
15. Активті екіұштық теоремасы.Теореманың математикалық өрнегі. Кез-келген активті екі полюсті ЭҚК көзінің ж/е кірістік кедергінің тізбектей жалғасуымен көрсетіле алады. Бұл ЭҚК-нің мәні активті екі полюстік қысқыштарына қатысты есептелетін бос жүріс кернеуіне тең болады. Кірістік кедергі активті екі полюстіктен ЭҚК-ді алып тастау жолымен алынған пассивті екі полюстіктің эквиваленттік кедергісіне тең болады. 
16 Компенсация теоремасы
Теңгеру теоремасын түсіндіру үшін а,б,в сұлбалар келтірілген. Кез келген кедергіні ЭҚК көзіне ауыстыруға болады. Оның бағыты ток бағытына қарама қарсы және сол кедергідегі кернеуіне тең. Бұл теңгеру теоремасы. Дәлелдеу үшін б суретінде д нүктесінен с нүктесіне өткенде әуелет(потенциалдар) E11=U1 шамасына көбейеді. Ал с нүктесінен в нүктесіне өткенде сол шамаға азаяды, осының салдарынан әлеует бір бірәне тең.сондықтан осы нүктелерді өткізгішпен тұйықтап қосуға болады,яғни ЭҚК көзі және кедергісі сұлбадан алып тасталынған бұдан басқа барлық тармақтағы ток өзгермейді. 
17.Синусоидалы ток тізбектері.Синусоидалы шамалар. Синусоидалы - деп sin заңы б/ша өзгеретін ж/е уақыт б/ша өзгер-н токты айт-з. Синусоидалық токтың лездік мәні мына өрнек-н анық-ды:i=Imsin(2πt/T+ψ)= Imsin(ωt+ψ), мұнд Im –ток амплитудасы, яғни токтың ең үлкен мәні; синус аргументі 2πt/T+ψ–фаза д.а. Бұрыш ψ-бастапқы уақыт мезгіліндегі (t=0) фазасына тең, сонд-н оны бастапқы фаза д.а.Синусоидалы ток тізб-ң элемент-і:1.активті кедергі R;Бұл токтың лездік кернеуі u=Umsinωt.Ом заңы б/ша u=iR=ImRsin ωt; Тұж-а: активті кедергіде ток пен кернеу фаза б/ша сәйкес келеді.активті кедергіге келіп түсетін қуат келесі өрнекпен анықт-ы: P=ui=UmsinωtImsinωt=UIsin2ωt=UmIm(1-cos2ωt)/2. Син-ы ток тізб-і индуктивтілік: ХL=ωL=2πfL; UL=LdI/dt кернеу-ң лездік мәні. Индуктивтіліктегі кернеу векторы ток векторынан 90̊ озып отырады. Сыйымдылық кедергі: Хс=1/ωС; u=1/c 0ʃπίdt. Сыйымд-қ кедергіде ток векторы кернеу вект-н 90̊-қа озады.
Синусоидалыэлектршамалар – электр тізбекте кернеудің және токтын лездік шамалары тең уакыт аралык саиын каиталанатын процесс периоды деп аталады.Периодты шаманын мәні кайталанатын ен аз уакыты период деп аталады.Синусоидалы шаманын озгеріп тұрган мәнін белгілейтін шама 
фаза депаталады.Уакытагымыбойынша фаза оседі. 2πшамага фаза оскенненкеинсинусойдалышаманынозгеру циклі каиталанады
18. Aктивті кедергідегі синусоидалы тоқ. Активті кедергідегі тоқ, кернеу, қуат(лездік және кешенді түрлері). Лездік мәндер графигі. Векторлық диаграммасы.
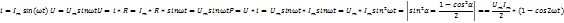
19.Индуктивтіктегі синусоидалы тоқ.
Кернеудің лездік мәні 
(индуктивтілік кешенді кедергі)
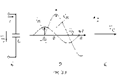
20.Сыйымдылықтағы синусоидалы тоқ.
Егер де С сыйымды лықтағы кернеу синусойдалы болса, 
онда тоқ:
көрініс көрініс көрсетіп тұр: тоқ 
ынта салынған кернеуден 
бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.Фазалық ығысу: 
–сыйымдылық кедергі, ал оған кері шама bC= 
– сыйымдылық өткізгіштік деп аталады. Сонымен, 
Сыйымдылықтағы лезді қуат:
Бұл қуат амплитудасы UI, ал бұрыштық жиілігі 2 
тең синусойдалы заң бойынша тербеленеді, яғни көрініс 
сияқты. Сыйымдылықтың электр өрісінің энергиясы:
0-ден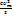 
– ге дейін шектерде бұрыштық жиілігі 
-мен периодикалы өзгеріп тұрады.
Көзбен сыйымдылықтың арасында энергияның тербеленуі өтеді, ал сыйымдылыққа түсетін активтік қуат нөлге тең. Сыйымдылық кедергіні былай табуға болады: 
21.Синусойдалы шамалардын лездик жане комплекс турлери:
Лездиктури: 
, 
, 
Комплекс тури: 
, 
, 
Кернеу мен Токтын арекет мани: 
, 
, 
, 
, 
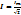
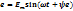Орташа мандери: 
, 
, 
22. R,L,C элементтерініің тізбектей жалғануы. Векторлық диаграммасы. 
; 
u=uR+uL+uC
u=i*R+L*di/dt+1/cʃidt
U=I*R+I*jXL+I*(-jXc)= I(R+j(Xl-Xc));
