Эпсилон - производительность непрерывного источника сообщений. Под конкретным непрерывным сообщением 
(t) подразумевают некоторую реализацию случайного процесса длительностью Т. Источник непрерывных сообщений характеризуется ансамблем его реализаций. Наиболее плодотворной оказалась модель непрерывного сообщения в виде эргодического случайного процесса.
Для определения производительности источника непрерывных сообщений воспользуемся подходом и результатами § 3.7, где определена ε-энтропия случайной величины.
Под ε-производительностью источника непрерывных сообщений Ηε(z) понимают минимальное количество информации, которое необходимо создать источнику в единицу времени, чтобы любую реализацию (t) можно было воспроизвести с заданной вероятностью ε.
Допустим, что (t) воспроизводится реализацией uT(t). Наблюдаемые реализации следует рассматривать, как сигналы, обладающие ограниченным, хотя возможно и достаточно широким спектром F [28, 8].
При достаточно большой длительности Т как (t), так и uT(t) могут быть представлены N-мерными (N = 2FT) векторами (
) и (
), координатами которых являются отсчеты. Ансамбли сообщений { (t)} и воспроизводящих сигналов {uT(t)} характеризуют при этом N-мерными случайными векторами Ζ и U, составляющими которых являются соответственно случайные величины Ζ1, Z2,.., ZN и U1, U2,.., UN. Статистическое описание каждого из ансамблей задается N-мерными плотностями распределения вероятностей ρ(Ζ) = ρ() и p(U) = p(). Связь между ансамблями отражают условные плотности распределений pu(Z)= = ρ( / ) и pz(U) = p( / ), а также совместная плотность распределения вероятностей p(Z,U) = p(; ).
Распространяя формулу (4.20) на N-мерные случайные векторы Ζ и U для количества информации одного из них относительно второго, получим
где интегралы являются N-мерными.
Используем, как и ранее, среднеквадратический критерий верности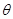 
(Z,U), который в рассматриваемом случае имеет вид
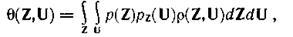
где p(Z,U)ZU представляет собой квадрат расстояния l(Z,U) в N-мерном евклидовом пространстве.
Количество информации, приходящееся в среднем на один отсчет дискретизованных сигналов ZT(t) и UT(t), определяется выражением
Тогда в соответствии с определением для ε-пропорциональности источника непрерывных сообщений Нε(Z) запишем
при выполнении условия
Величина ν характеризует скорость формирования источником отсчетов (ν = =2F).
Пример 4.5. Определить ε-производительность источника, формирующего со скоростью ν1 некоррелированные отсчеты стационарного нормального случайного сигнала с дисперсией σ2.
Воспользовавшись полученным в (3.65) значением ε-энтропии для нормально распределенной случайной величины, найдем
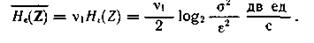
Возможности воспроизведения любого сообщения zT(t) с заданной верностью можно дать геометрическое толкование. Поскольку все реализации эргодического процесса достаточно большой длительности являются типичными и обладают практически одной и той же средней мощностью, концы соответствующих им векторов в N-мерном пространстве сообщений составляют непрерывное множество точек, равноудаленных от начала координат (гиперсферу).
Конечное подмножество воспроизводящих сигналов UT(t) размещается в центрах непересекающихся правильных сферических N-угольников (ε-областей), на которое гиперсфера разбивается без промежутков. Размеры ε-областей определены заданной верностью воспроизведения сообщений. Если источником реализуется сообщение z*T(t), конец вектора которого должен попасть в ε-область сигнала u*T(t), то воспроизводится сигнал u*T(t).
Следует отметить, что заданная верность воспроизведения будет достигнута с вероятностью, близкой к единице, только при достаточно большой длительности сообщений, когда погрешностью от замены непрерывных реализаций последовательностями отсчетов можно будет пренебречь. Для уменьшения указанной погрешности при ограниченной длительности сообщений Т необходимо увеличивать число отсчетов N. В пределе при N→∞ получим непрерывные реализации.
В вычислении ε - производительности источника и геометрическом толковании возможности воспроизведения сообщений с заданной верностью принципиально ничего не изменяется. Следует лишь учесть, что N-мерное евклидово пространство сообщений становится гильбертовым и мерой близости двух сигналов должно быть расстояние в этом пространстве.
