Розв’язання систем линійних алгебраічних рівнянь

Вступ

У сучасному світі персональних комп'ютерів електронні таблиці,подібні Excel, стали таким же звичайним явищем, як текстовіпроцесори і комп'ютерні ігри. Однак це не означає, що їх добре знаютьі ефективно використовують.

Як нам вже відомо, Excel є організатором будь-якого типуданих - числових, текстових і інших - і оскільки в даній програміє безліч обчислювальних можливостей, то часто користувачізвертаються до неї, коли необхідно створити таблиці для фінансових розрахунків.Не меншою популярністю користуються і можливості Excel, які служать для побудови діаграм, будь-яких видів, і графіків. Excel без праці перетворює нудні чорно -білі стоки та стовпці в яскраві і барвисті графіки та діаграми.

Крім усього вище сказаного, не слід випускати з уваги той факт, що Excel - чудовий хранитель баз даних і творець таблиць. Саме по цього дана програма як не можна краще підходить для відстеження інформації про що продаються товари, що обслуговуються клієнтів і т.п.

Як ми бачимо, можливості Excel дуже великі і для їх розгляду було б потрібно багато часу, але дана задача перед нами і не варто: у цій роботі ми звернемо свою увагу на майстра функцій, дізнаємося його призначення та порядок роботи з ним.

Масиви в Excel використовують для створення формул, які повертають деяке безліч результатів або оперують безліччю значень.

Робота з масивами даних

В Microsoft Excelможна обчислювати значення не лише для аргументів, які знаходяться в окремих комірках, але й одночасно для цілих діапазонів комірок, тобто масивів. Згадаємо з математики, що масив — це впорядкований набір елементів (тобто кожен елемент сукупності має свій порядковий номер — адресу).

Масиви бувають одномірні (вектори),двомірні (матриці), тримірні і т.д. В електронних таблицях Excelможна виконувати операції лише над одномірними та двомірними масивами (векторами та матрицями). Програма дозволяє виконувати обчислення з усіма даними виділеного діапазону. При цьому використовується формула масиву. Вона відрізняється від звичайної формули тим, що записана у фігурних дужках, які і виступають ознакою формули масиву.

Excel дозволяє будувати формули, результатом обчислення яких є не одне скалярне значення, а цілий масив (сукупність) значень. Наприклад, у множину вбудованих функцій входять функції для роботи з матрицями: обчислення добутку матриць, оберненої матриці. Можна записати і свої власні формули, що застосовуються до діапазонів комірок, результатом обчислення яких буде діапазон комірок. Наприклад, =F4:F9–G4:G9.

Для обчислення елементів масиву в Excelвикористовується єдина формула на всі елементи масиву. Результатом введення такої фомули масиву беде те, що в кожній комірці діапазону комірок буде знаходитись формула у фігурних дужках.

Коли фігурні дужки ввести вручну (з клавіатури), то бажаного результату користувач не отримає (введена формула буде сприйматись як звичайний текст).

Для введення формул масиву необхідно:

 

· Виділіти діапазон комірок, що повинні містити результати обчислення формули масиву. Розмірність виділеного діапазону повинна відповідати кількості значень, що повертаються формулою.

· Ввести потрібну формулу, вказуючи посилання на діапазони комірок, що повинні використовуватися в обчисленнях.

· Завершити уведення формули натисканням сполучення клавіш “Ctrl+Shift+Enter” (а не “Enter”як в звичайних формулах).

· Excel помістить формулу масиву у фігурні дужки, що є ознакою формули масиву. У комірках виділеного діапазону будуть представлені результати обчислення формули.

 

Excel завжди інтерпретує масив як єдине ціле та не дозволяє змінити окремі клітинки масиву. Проте можна задати для окремих клітинок різноманітні параметри форматування. Клітинки не можуть бути переміщені з масиву, а нові клітинки — добавлені у масив.

Масиви констант можна використовувати замість посилань, якщо небажано вводити кожне значення константи в окрему клітинку аркуша.

Деякі вбудовані функції є формулами масиву. Для отримання належних результатів їх слід вводити як масиви.

Формула масиву для обчислення окремого результату спрощує модель аркуша, замінює декілька окремих формул на одну формулу масиву.

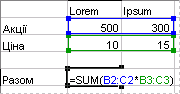
Наприклад, далі обчислюється підсумкове значення цін на акції, при цьому не використовується рядок комірок для обчислення та відображення окремих значень для кожної акції.

Мал. 1. 1.

Формула масиву для обчислення окремого результату. Якщо формулу ={SUM(B2:D2*B3:D3)} введено як формулу масиву, вона перемножує значення “Акції” та “Ціна” для кожної біржі, а потім підсумовує результати цих обчислень.

Формула масиву для обчислення декількох значень. Деякі функції повертають масиви значень або запитують масиви значень як аргумент. Щоб обчислити декілька значень за допомогою формули масиву, потрібно ввести масив у діапазон комірок, який має таку саму кількість рядків і стовпців, що й аргументи масиву.

Наприклад, за вказаним рядом із трьох значень продажу (стовпець В) і рядом із трьох місяців (стовпець А) функція TREND визначає продовження лінійного ряду обсягу продажу. Для відображення всіх обчислюваних значень формулу введено у три клітинки стовпця C (C1:C3).

Мал. 1. 2.

Формула масиву для обчислення декількох значень. Формула =TREND(B1:B3;A1:A3), введена як формула масиву, повертає три значення (22196, 17079 і 11962), обчислені за трьома обсягами продажу за три місяці.

Для виконання табличних обчислень потрібні формули. Оскільки деякі формули і їхні комбінації зустрічаються дуже часто, те програма Excel пропонує більш 400 заздалегідь вбудованих формул, що називаються функціями. Розглянемо деякі з них.

Функція ПРОСМОТР

Функція ПРОСМОТР повертає значення зі строки, стовбцю чи масива залежно від використовуваної синтаксичної форми: «вектор» чи «масив».

Вектор – це інтервал, що містить тільки один рядок або стовпец. Векторна форма функції ПРОСМОТР переглядає діапазон, до якого входять значення тільки одного рядка чи стовпця (так званий вектор), у пошуках певного значення та повертає значення з тієї ж позиції другого діапазону.

Векторна форма функції ПРОСМОТР використовується для перегляду значень у великому списку чи значень, що помінялися з часом.

Синтаксис для векторной форми. ПРОСМОТР(шукане_значення, переглядаїмий_вектор, вектор_результатів)

Таблиця 2.1. Аргументи векторної форми функції ПРОСМОТР

Найменування	Значення	Примітка
шукане_ значення	Значення, яке функція шукає у першому векторі	Аргумент може бути числом, текстом, логічним значенням, ім’ям чи силкою, що вказує на значення. Якщо функція не може знайти шукане значення, то підходить найбільше значення в аргументі переглядає мий_вектор, котре менше чи дорівнює шуканому_значенню Якщо шукане_значення менше, ніж найменше значення в аргументі переглядає мий_вектор, функція повертає значення помилки #Н/Д
переглядаємий_вектор	Інтервал, що містить лише один рядок чи стовпець.	Аргумент може бути числом, текстом, логічним значенням. Значення аргументу мають бути розміщені у порядку зростання
вектор_результатів	Інтервал, що містить лише один рядок чи стовпець.	Аргумент повинен мати той же розмір, що і переглядаємий_вектор

Рис 2.1 Діалогове вікно векторної форми функції ПРОСМОТР

 

Форма масив використовується для перегляду невеликого списку значень, котрі залишаються постійними з плином часу. Ця форма функції ПРОСМОТР призначена для забезпечення сумісності з іншими програмами електронних таблиць.

Форма «масив» переглядає перший рядок та стовпець масива, знаходить вказане значення та повертає значення з аналогічної позиції останнього рядка чи стовпця масива.

Синтаксис форми масив. ПРОСМОТР(шукане_значення; масив)

Таблиця 2.2 Аргументи форми «масив» функції ПРОСМОТР

Найменування	Значення	Примітка
шукане_ значення		Аргумент може бути числом, текстом, логічним значенням, ім’ям чи силкою, що вказує на значення. Якщо функція не може знайти шукане значення, то підходить найбільше значення в аргументі масив, котре менше чи дорівнює шуканому_значенню Якщо шукане_значення менше, ніж найменше значення у першому рядку чи стовпці, функція повертає значення помилки #Н/Д
масив	Інтервал, що містить текст, числа чи логічні значення, які потребують порівнянння.

 

Рис 2.1 Діалогове вікно форми «масив» функції ПРОСМОТР

Функція ВПР

Функція ВПР, мабуть, одна з найкрасивіших функцій в наборі Excel. Варіантів її застосування безліч. Основне застосування - пошук збігів у різних списках (порівняння баз даних). Синтаксис написання формули наступний:= ВПР (A1; База_данних; 2; БРЕХНЯ)

Розглянемо параметри функції ВПР:

A1 - це відносне посилання на клітинку аркуша Excel, в якій знаходиться шукане значення. Під відносною посиланням розуміється те, що при копіюванні формули по стовпцях / рядкам посилання буде змінюватися відповідно. Щоб при копіюванні формули в інші стовпці / рядки посилання на стовпець / рядок змінювалася її можна зробити абсолютної по одному / обома параметрами. Наприклад:

· $A$1 - абсолютна посилання по стовпці і по рядку;

· $A1 - абсолютна по стовпці, відносна по рядку;

· A$1 - відносна по стовпці, абсолютна по рядку;

· A1 - відносне посилання по стовпці і рядку.

Значок $ можна вставити у формулу вручну, або виділити в рядку формул посилання і послідовно натискаючи F4 домогтися потрібного результату.

База_данних - ім'я області даних в першому стовпці якої, проводиться пошук збігів значення з параметром A1. Стовпець за яким здійснюється пошук завжди має бути першим. Область даних можна також задати вказавши адресу лівої верхньої і правої нижньої комірки. наприклад: = ВПР (A1; Лист2! A1: H30; 2; БРЕХНЯ)

У наведеному прикладі посилання на область даних відносна, це означає що при копіюванні формули адреса області даних буде змінюватися, що призведе до помилок, тому посилання треба робити абсолютною. наприклад: = ВПР (A1; Лист2! $ A $ 1: $ H $ 30; 2; БРЕХНЯ)

Звичайно відносна посилання на область даних виходить автоматично, якщо область даних вказується виділенням і знаходиться в тій же книзі (файлі) де і прописується формула. Якщо область даних знаходиться в іншій книзі (файлі) то посилання на цю область автоматично проставляється абсолютної при виділенні області. Це корисно пам'ятати, щоб вчасно звернути увагу на вміст формули і якщо необхідно внести виправлення.

Параметр БРЕХНЯ означає що функція ВПР буде шукати точний збіг значення в комірці A1 зі значеннями в першому стовпці області даних. При знаходженні такого значення функція поверне значення із заданого стовпця (в даному прикладі - другий стовпець) області даних. Якщо значення A1 не знайдено, функція ВПР поверне # Н / Д - немає даних. Другим значенням цього параметра може бути ІСТИНА. У цьому випадку функція ВПР буде шукати найближче до шуканого значенням A1. Чесно кажучи механізм визначення цього найближчого значення до кінця не ясний, особливо коли шукане значення текст. Тому застосування функції ВПР з параметром "ІСТИНА" зустрічається досить рідко.

Приклад.

Мал. 3.1 Приклад функції ВПР

У прикладі області даних A1: D9 присвоєно ім'я База_данних. Функція ВПР () із зазначеної області повертає дані зі стовпців 1-4 спираючись на унікальний ідентифікатор (ключ) в стовпці A. Як видно з прикладу область даних можна задати як через ім'я, так і діапазоном, залежно від того, як зручніше в конкретному випадку. В останньому випадку діапазон зручніше задавати абсолютними посиланнями $ A $ 6: $ D $ 9, ніж відносними A6: A9, тоді при копіюванні формули по осередках адресу діапазону мінятися не буде.

 

Функція трансп

Бувають ситуації, коли вам необхідно транспонувати дані однакового діапазону, тобто однакової кількості значень. Наприклад, вам часто доводиться перетворювати дані з продажу по місяцях у вигляді горизонтальної таблиці у вертикальну як на малюнку.

Мал. 4.1

Звичайно, ви можете кожен раз використовувати спосіб розглянутий нами раніше, але в деяких випадках можна спростити завдання і зробити так, щоб дані транспоновану у вертикальну таблицю автоматично.

Це можна зробити за допомогою формули ТРАНСП. Синтаксис цієї функції дуже простий ТРАНСП(масив), де масив це діапазон даних, які необхідно перетворити у вертикальний або горизонтальний вигляд (транспонувати).

Для реалізації даного способу нам необхідно вибрати діапазон в якому автоматично будуть транспонуватися дані. У нашому випадку це C8: C13.

Мал. 4.2

Після цього на клавіатурі відразу набираєте формулу = ТРАНСП (С3: H3)

В результаті у вас має отримати наступне:

Мал. 4.3

Далі, набравши формулу необхідно натиснути одночасно (Ctrl + Shift + Enter) для застосування формули масиву. У результаті формула з двох сторін буде оточена фігурними дужками.

Важливо розуміти, що якщо ви просто вкажіть фігурні дужки, то функція ТРАНСП працювати не буде. Крім того масиви (діапазони) повинні бути однакової величини.

Тепер змінюючи дані в горизонтальній таблиці, вони автоматично будуть змінюватися у вертикальній таблиці.

 

Розв’язання систем линійних алгебраічних рівнянь

Табличні формули або формули масиву - дуже потужний обчислювальний засіб Excel, що дозволяє працювати з блоками робочого листа як з окремими осередками. Табличні формули в якості результату повертають масив значень. Тому перед введенням такої формули необхідно:

· виділити діапазон осередків, куди будуть поміщені результати;

· набрати формулу;

· після закінчення введення натиснути комбінацію клавіш Ctrl+Shift+Enter

Формула вводиться в усі осередки виділеного інтервалу. При активізації будь-якого осередку з інтервалу, що містить формулу масиву, в рядку формул відображається введена формула, поміщена у фігурні дужки. Саме фігурні дужки є ознакою табличної формули. Для виділення усього блоку, що містить табличну формулу, необхідно виділити один з його осередків, після чого натиснути комбінацію клавіш Ctrl+/. Неможливо редагувати вміст тільки одного осередку з інтервалу з табличною формулою. Змінити можна тільки увесь блок цілком, для чого він і має бути заздалегідь виділений.

До найпростіших операцій з матрицями прийнято відносити наступні:

· додавання і віднімання матриць,

· множення і ділення матриці на число,

· перемножування матриць,

· транспонування,

· обчислення оберненої матриці.

Множення (поділ) матриці на число, додавання (віднімання) матриць в Excel реалізуються досить просто: за допомогою звичайних формул (поелементне додавання чи віднімання, множення або ділення на число), або з використанням табличних формул, як це описано нижче.

Складання матриць. Наприклад, нехай необхідно скласти дві матриці розміру 3х3.

Елементи першої матриці(9 елементів) розмістимо в інтервалі A1: C3, другий, - в діапазоні E1: G3. Під результат виділимо інтервал A5: C7. Після чого, не знімаючи виділення, введемо формулу =A1: C3+E1: G3, натиснувши комбінацію клавіш Ctrl+Shift+Enter. У осередках інтервалу A5: C7 відобразиться результат - сума відповідних елементів матриць, а в рядку формул ми побачимо {=A1: C3+E1: G3}.

Множення матриці на число. Нехай замість складання нам потрібно помножити першу матрицю на число 2. Для цього переміщаємося всередину інтервалу A5: C7, виділяємо його, натиснувши комбінацію Ctrl+/, вносимо у формулу виправлення =A1: C3*2 і натискаємо Ctrl+Shift+Enter. У інтервалі A5: C7 побачимо результат множення, а в рядку формул - табличну формулу {=A1: C3*2}.

 

Для інших матричних операцій в Excel передбачені функції:

МОПРЕД(матриця)	обчислення визначника матриці
МОБР(матриця)	обчислення зворотної матриці
МУМНОЖ(матрица1;матрица2)	добуток матриць
ТРАНСП(матриця)	транспонування матриці

 

Приклад. Для вирішення системи:

представимо цю систему в матричному вигляді: AX = B, де А – матриця коэффіцієнтів системы рівнянь, Х – вектор невідомих та В – вектор правых частей.

У цьому випадку невідомі x₁,x₂, x₃ и x₄ рахуються за формулою:

,i=1, …, 4

Де ∆ - визначник матриці A, ∆_i - визначник матриці, що виходить з матриці А шляхом заміни i-го стовпця вектором b.

Решение СЛАУ можно найти по формулам Крамера:

Де det А = |А| - визначник матриці системи (гголовний визначник), det А_i = |A_i|

(i=1, 2,..., n) - визначники матриці, (допоміжні визначники), котрі виходять з А заміною i-го стовпця на стовпець вільних членів В. Лінійна алгебраічна система несумісна (не має розв’язків), якщо det А = 0.

Мал. 5.1

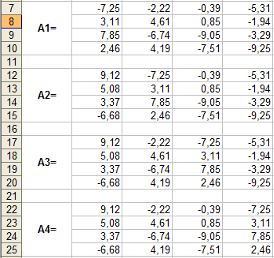
Для реалізації цього методу в MS Excel:

1. введемо матрицю А та вектор b на робочий лист.

2. Зформируємо чотири допоміжні матриці, замінюючи послідовно стовпці матриці A на стовпець вектора b (мал.. 5.1).

3. Щоб вичислити визначник матриці A. Встановимо курсор в ячейку H8 та зверннемося до майстра функцій. У категориї Математичні оберемо функцію МОПРЕД, що призначену для обчислення визначника матриці, та перейдемо до другого кроку майстра функцій. Діалогове вікно, що з’являється на другому кроці містить поле ввода Масив. В цьому полі указують диапазон матриці, визначник якої обчислюють. У нашому випадку це ячейки B2:E5. (Мал. 5.2)

 

Мал. 5.2

4. Для обчислення допоміжних визначників введем формулы:

H9=МОПРЕД(B7:E10),

H10=МОПРЕД(B12:E15),

H11=МОПРЕД(B17:E20),

H12=МОПРЕД(B22:E25).

У результаті в комірці H8 зберігається головний визначник, а в осередках H9: H12 - допоміжні.

5. Скористаймося формулами Крамера і розділимо послідовно допоміжні визначники на головний. У осередок J9 введемо формулу = H11 / $ H $ 8. Потім скопіюємо її вміст в осередку J10, J11 і J12.

6. Зробимо перевірку рішення, для цього підставимо в нашу систему отримані значення:

7. У осередок L9 вводимо формулу = B2 * $ J $ 9 + C2 * $ J $ 10 + D2 * $ J $ 11 + E2 * $ J $ 12. Потім копіюємо її вміст в осередку L10, L11 і L12, отримані в результаті обчислень відповіді співпали з відповідями у вихідному прикладі - Система вирішена вірно

Матричний спосіб вирішення СЛАР. Цей спосіб досить простий. Обидві частини матричного рівності АХ = В помножимо зліва на обернену матрицю А-1:

A^-1AX = A^-1B.

 

Так як A^-1A = Е, где Е - одинична матриця (діагональна матриця, у якої по головній діагоналі розташовані одиниці), то рішення системи

X = A^-1В.

Тобто для вирішення системи необхідно знайти для матриці А зворотний A-1 і помножити її праворуч на вектор-стовпець В вільних членів.

Розглянемо рішення системи матричним способом.

1. Введемо матрицю А у ячейки B28: E3.

2. Осередки діапазона G28: G31 запвнюємо значеннями правых частин рівнянь системы:

Мал. 5.3

3. В осередку B33 щоб обчислити визначник матриці А, викликаємо Майстер функцій і в категорії Математичні клацнемо на імені функції МОПРЕД, яка повертає величину визначника матриці. Відкриється діалогове вікно Аргументи функції для функції МОПРЕД. У полі Масив вказуємо діапазон комірок G28: G31..

4. Виділяємо діапазон осередків E33: E36, призначений для відображення знайденого рішення.

5. Помістимо курсор в рядок формул і викличемо Майстер функцій. Вибираємо функцію МУМНОЖ, яка повертає результат множення матриць і заповнюємо діалогове вікно Аргументи функції наступним чином:

Мал. 5.4

 

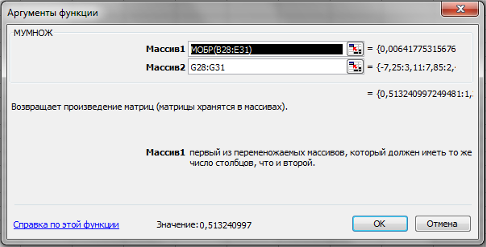
6. Завершіть введення формули не традиційним клацанням на кнопці OK, а комбінацією клавіш Ctrl Shift Enter. Натискати їх слід послідовно і не відпускати 1-2 секунди, поки не зафіксується одночасне натискання всіх трьох клавіш. Фрагмент електронної таблиці, що реалізує рішення, наведений на малюнку.

Мал. 5.5

 

Висновки

Табличний процесор Excel фірми Microsoft призначений для введення, зберігання, обчислення і виведення великих обсягів даних у вигляді, зручному для аналізу і сприйняття інформації. Усі дані зберігаються й обробляються у вигляді окремих або зв'язаних таблиць.

Сучасні табличні процесори, зокрема Microsoft Excel, являють собою надзвичайно потужний засіб за рішенням широкого діапазону завдань: від проведення найпростіших розрахунків до створення засобів автоматизації обчислень.

Вивчення можливостей таких програм може принести студентам безсумнівну користь при самостійному опрацюванні навчального матеріалу.

 

Список літератури

1. Вєдєнєєва Е.А. Функції та формули Excel 2007. Бібліотека користувача. -СПб.: Питер, 2008. -384 С.: Ил.

2. М. Додж, К. Кіната, К. Стінсон "Ефективна робота м Microsoft Exsel 97 ", видавництво" Пітер "; Санкт-Петербург, 1998р.

3. Є.К. Овчаренко, О.П. Ільїна, Є.В. Балибердін "Фінансово - економічні розрахунки в Exsel", Москва, 1999 р.

4. Шеррі Кінкоф; пров. з англ. А. Г. Парфьонов., Microsoft Excel 2000. - М.: АСТ: Астрель, 2006.