ЛЕКЦИЯ 3.
Решение задач по теме «Векторная алгебра»
Найти орт и направляющие косинусы вектора a{-4; 3; 12}.
Решение. Длина вектора 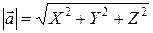 ;
;  .
.
Орт вектора  :
:  ;
;
Направляющие косинусы: 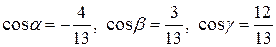 .
.

Проверить, являются ли векторы и А) коллинеарными; Б) ортогональными.
Решение. А) 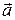 úç
úç  Û
Û 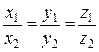 . Имеем:
. Имеем:  Þ
Þ 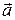
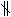
 .
.
Б) 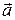 ^
^  Û
Û  . Считаем:
. Считаем: 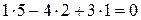 Þ
Þ 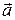 ^
^  .
.
Вычислить скалярное произведение векторов и, если,,,, угол между векторами и равен 60°.
Решение. Как решить задачу?
Формула 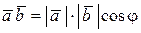 (определение скалярного произведения) не применима, поскольку неизвестны длины векторов
(определение скалярного произведения) не применима, поскольку неизвестны длины векторов 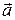 и
и  и угол между ними.
и угол между ними.
Формула  (скалярное произведение в координатах) также не подходит, т.к. неизвестны координаты векторов.
(скалярное произведение в координатах) также не подходит, т.к. неизвестны координаты векторов.
Воспользуемся свойствами линейности и коммутативности скалярного произведения:
 =
=
(далее используем определение скалярного произведения для векторов  и
и 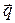 )
)
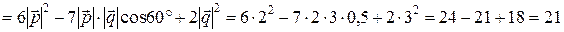 .
.
В кубе найти угол между диагоналями и.
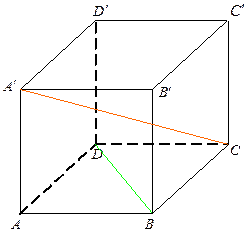
Решение. Построим прямоугольную систему координат OXYZ. Начало координат совместим с вершиной А, ось ОХ направим вдоль АВ, ось OY – вдоль AD, ось OZ – вдоль 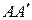 . Пусть длина стороны куба равна 1. Тогда
. Пусть длина стороны куба равна 1. Тогда  ,
,  ,
,  - орты осей координат.
- орты осей координат.
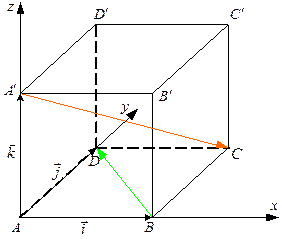
Рассмотрим векторы 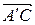 и
и 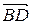 . По правилу сложения и вычитания векторов
. По правилу сложения и вычитания векторов
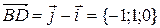 ;
;  .
.
Вычисляем косинус угла между векторами по формуле
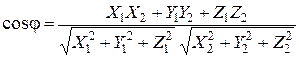 :
:
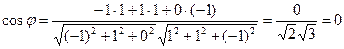 .
.
Находим угол:
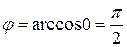 .
.
В треугольнике ABC с вершинами A(1,2,3), B(-1,0, 4), C(4,2, -1) найти длину высоты BD.
Решение.
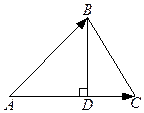
Идея решения задачи. Выразим площадь треугольника двумя способами: по стандартной школьной формуле 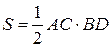 и через векторное произведение
и через векторное произведение 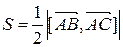 . Приравнивая площади, найдем высоту BD.
. Приравнивая площади, найдем высоту BD.
1. Находим координаты векторов 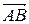 и
и  (из координат конца вычитаем координаты начала):
(из координат конца вычитаем координаты начала):
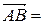 {-1-1;0-2;4-3}={-2;-2;1};
{-1-1;0-2;4-3}={-2;-2;1};  ={4-1;2-2;-1-3}={3;0;-4}.
={4-1;2-2;-1-3}={3;0;-4}.
2. Находим векторное произведение в координатах по формуле
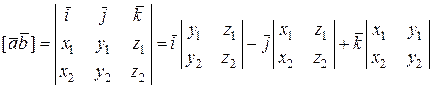 .
.
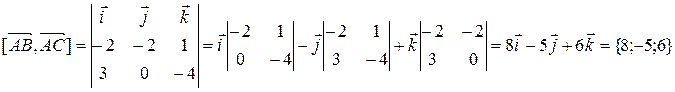 .
.
3. Модуль (длина) векторного произведения вычисляется по формуле 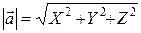 :
:
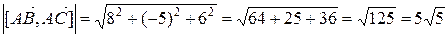 .
.
4. Площадь треугольника ABC равна
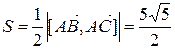 .
.
5. Находим длину основания:
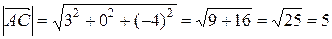 .
.
6.Из формулы для площади треугольника
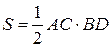
находим длину высоты BD:
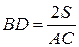 ;
; 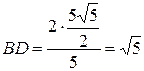 .
.
Найти координаты вектора длины, перпендикулярного векторам {-1;2;-2} и {1;2;4}, и образующего тупой угол с осью OX.
Решение. 1 способ (с использованием скалярного произведения). Обозначим неизвестные координаты вектора  . Два условия перпендикулярности векторов (
. Два условия перпендикулярности векторов ( ) и заданная длина (
) и заданная длина (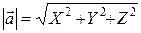 ) позволяют составить систему 3 уравнений с 3 неизвестными. Решая систему, находим координаты вектора. Сделать самостоятельно.
) позволяют составить систему 3 уравнений с 3 неизвестными. Решая систему, находим координаты вектора. Сделать самостоятельно.
2 способ (с использованием векторного произведения). Воспользуемся определением: векторное произведение – это вектор, ортогональный обоим векторам-сомножителям. Поскольку два перпендикуляра к плоскости параллельны, векторное произведение 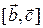 есть вектор, коллинеарный вектору
есть вектор, коллинеарный вектору 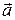 . Координаты коллинеарных векторов пропорциональны:
. Координаты коллинеарных векторов пропорциональны: 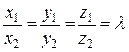 , коэффициент пропорциональности l найдем как отношение длин векторов.
, коэффициент пропорциональности l найдем как отношение длин векторов.
Переходим к вычислениям.
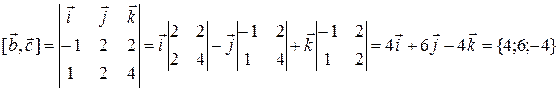 ;
;
условие пропорциональности координат позволяет выразить неизвестные через l:
 Þ
Þ 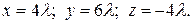
Длина вектора 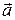 равна
равна
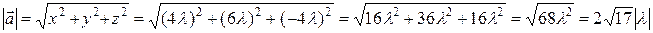
(не забудем модуль: 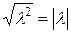 ).
).
Находим величину l из условия 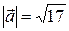 :
:
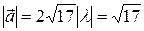 Þ
Þ 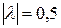 , Þ
, Þ 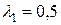 ;
;  .
.
Координаты вектора 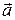 равны:
равны:
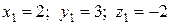 или
или 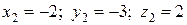 .
.
Итак, мы нашли два вектора: 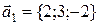 и
и  . Они оба перпендикулярны векторам
. Они оба перпендикулярны векторам  и
и 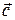 , и имеют заданную длину
, и имеют заданную длину  . Осталось последнее условие: вектор
. Осталось последнее условие: вектор 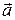 образует тупой угол с осью OX. Это означает, что
образует тупой угол с осью OX. Это означает, что
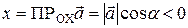 (во второй четверти косинус отрицателен).
(во второй четверти косинус отрицателен).

Следовательно, данному условию удовлетворяет второй вектор  . Ответ:
. Ответ: 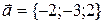 .
.






