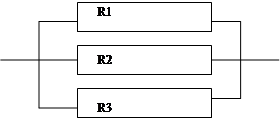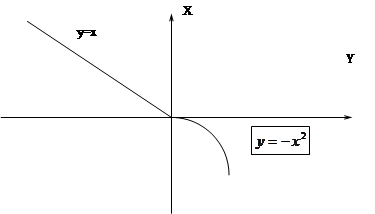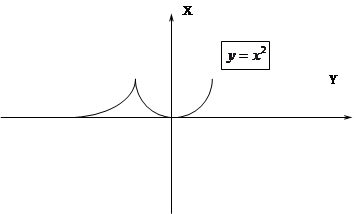Оператор присваивания
1. Составить программу вычисления значения функции:
a) 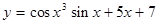 b)
b) 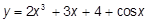 c)
c) 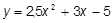
d)  e)
e)  f)
f) 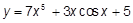
g)  h)
h)  i)
i) 
j) 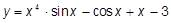 k)
k) 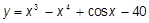 l)
l) 
m) 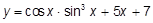
2. Записать операторы присваивания, которые переменной d присваивают:
| a) среднее арифметическое чисел x, y, z; | b) площадь треугольника со сторонами а, в, с. |
3. Записать оператор присваивания, который меняет знак у значения переменной t.
4. Чему равны значения переменных x и y после выполнения операторов x:=2; y:=5; x:=y: y:=x?
5. Какое значение будет иметь переменная x после выполнения операторов x:=10; x:=x+3?
6. Дано действительное число. Найти куб этого числа.
7. Даны два действительных числа:
| a) Найти разность первого и второго; | b) Найти их произведение; |
| c) Найти среднее арифметическое этих чисел. | d) Найти их среднее геометрическое[1]. |
8. Даны три действительных числа:
| a) Найти их сумму; | b)Найти разность первого и третьего чисел, затем сложить со вторым |
9. Даны катеты прямоугольного треугольника. Найти гипотенузу.
10. Даны действительные числа x, y, z. Вычислить:
a) 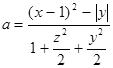 ; ;
| b) 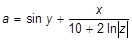
|
11. Дан радиус r окружности. Найти длину l окружности. Ответ вывести в следующем виде:
при радиусе r =... длина окружности l =...
12. Дана сторона равностороннего треугольника. Найти площадь этого треугольника (ответ вывести аналогично, как в задаче 11).
13. Даны x = 1, 2.1, 3, 10, -5. Найти значения функции
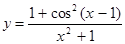
в этих точках. Ответ вывести в виде таблицы:
| X | Y |
| … | |
| 2.1 | … |
| … | |
| … | … |
14. Дан радиус круга. Найти площадь круга (ответ в виде таблицы, как в 13).
15. Вычислить расстояние между двумя точками с координатами (а, b) и (c, d).
16. Треугольник задан координатами своих вершин. Найти:
| a) периметр треугольника; | c) площадь треугольника |
17. Дано действительное число х. Используя только умножение, сложение и вычитание, вычислить 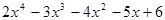 . Разрешается использовать не более 4-х умножений и
. Разрешается использовать не более 4-х умножений и
4-х сложений и вычитаний.
18. Даны действительные числа х и y. Используя только умножение, сложение и вычитание, вычислить
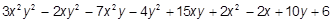
Разрешается использовать не более восьми умножений и восьми сложений и вычитаний.
19. Вычислить 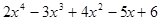 , используя не более четырех операций умножения и не более четырех операций сложения и вычитания. Никакие другие операции использовать нельзя.
, используя не более четырех операций умножения и не более четырех операций сложения и вычитания. Никакие другие операции использовать нельзя.
20. Вычислить 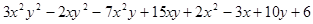 , используя не более восьми операций умножения и не более восьми операций сложения и вычитания. Никакие другие операции и функции использовать нельзя.
, используя не более восьми операций умножения и не более восьми операций сложения и вычитания. Никакие другие операции и функции использовать нельзя.
21. Вычислить  , используя не более восьми арифметических операций. Никакие функции использовать нельзя.
, используя не более восьми арифметических операций. Никакие функции использовать нельзя.
22. Дано действительное число а. Используя только умножение, получить  :
:
| a) при n=4 за 2 операции; | b) при n=6 за 3 операции; | c) при n=7 за 4 операции; |
| d) при n=8 за 3 операции; | e) при n=9 за 4 операции; | f) при n=10 за 4 операции; |
| g) при n=13 за 5 операций; | h) при n=15 за 5 операций; | i) при n=21 за 6 операций; |
| j) при n=28 за 6 операций; | k) при n=64 за 6 операций. |
23. Дано действительное число x. Используя только умножение, получить одновременно 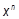 и
и 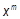 :
:
| a) при n=3 и m=10 за 4 операции; | b) при n=4 и m=20 за 5 операций; |
| c) при n=5 и m=13 за 5 операций; | d) при n=5 и m=19 за 5 операций. |
24. Давным-давно, открывая самые первые Олимпийские игры, Геракл отмерил расстояние в 600 своих ступней и назвал эту дистанцию стадием. Напишите программу, которая поможет определить чему же равен размер ноги Геракла. С помощью этой программы определите какой размер ноги мог быть у Геракла, если по разным источникам длина стадия колеблется от 186 до 192 метров.
25. Вы желаете приобрести прямоугольный участок земли площадью 500 м2. Каковы должны быть размеры этого участка, чтобы длина забора вокруг него была минимальной? Напишите программу, которая поможет Вам подобрать ответ на этот вопрос.
|
26. Из квадратного листа жести со стороной 1 метр вырезают заготовку для коробки, как это показано на рисунке. Т.е. вырезают по углам коробки маленькие квадратики, а затем сгибают полученную заготовку по пунктирным линиям и пропаивают. Напишите программу, которая поможет Вам подобрать глубину выреза так, чтобы объём коробки стал максимальным. Пользуясь этой программой найдите оптимальную глубину выреза.
27. Оказывается, что значения функции sin можно приблизительно вычислять по следующей формуле:
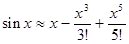
при чем, чем меньше значение аргумента, тем точнее приведенная формула. Напишите программу для вычисления приближенного значения функции  по этой формуле. Сравните полученные значения с точными[2].
по этой формуле. Сравните полученные значения с точными[2].
28. Оказывается, что значения функции cos можно приблизительно вычислять по следующей формуле:

при чем, чем меньше значение аргумента, тем точнее приведенная формула. Напишите программу для вычисления приближенного значения функции  по этой формуле. Сравните полученные значения с точными.
по этой формуле. Сравните полученные значения с точными.
29. Оптимальный вес человека может быть вычислен по формуле:
где T — окружность груди в сантиметрах, L — рост в сантиметрах, P — оптимальный вес в килограммах. Напишите программу для вычисления по этой формуле. Определите свой оптимальный вес.
30. Оптимальный вес человека в зависимости от его роста можно вычислить по формуле:

где P — вес в килограммах, L — рост в сантиметрах. Напишите программу для вычислений по этой формуле.
31. Известно, что 1 г. углеводов и белков дает 4 Ккал, а 1 г. жиров — 9. Составьте программу для подсчета килокалорий в рационе. Определите калорийность Вашего обеда.
32. Найти длину окружности, площадь круга и объем шара радиуса R.
33. По данным катетам найти гипотенузу и площадь прямоугольного треугольника.
34. Дано: 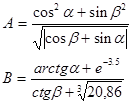 . Углы
. Углы  и
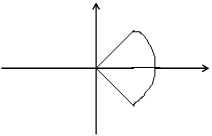
и 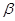 заданы в градусах. Найти значения A и B.[3]
заданы в градусах. Найти значения A и B.[3]
35. Дано:  . Углы
. Углы  и
и  заданы в градусах. Найти значения C и D.
заданы в градусах. Найти значения C и D.
36. Написать программу для решения системы линейных уравнений с двумя неизвестными: 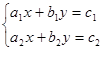 методом Крамера:
методом Крамера: 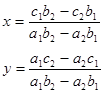 . Для просторы давайте считать, что
. Для просторы давайте считать, что  .
.
37. Составьте программу определения массы воздуха, находящегося в цилиндре дизельного двигателя объемом V при температуре T и давлении p.  ,
,
где p — давление газа, m — масса, V — его объем, T — температура, M — 0.029 кг/моль — молярная масса газа, R — 8,31441 Дж/(моль K) — газовая постоянная.
38. Написать программу для вычисления площади треугольника по двум сторонам и углу между ними.
39. Вычислить объем усеченного конуса и его образующую по высоте и радиусам оснований.
40. Вычислить Z=X+Y, где 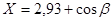 , а
, а 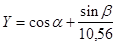 , если углы
, если углы  и
и 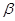 задаются в градусах.
задаются в градусах.
41. Вычислить C=D-K, где 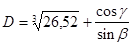 , а
, а 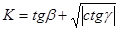 , если углы
, если углы  и
и 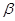 измеряются в градусах.
измеряются в градусах.
|
42. Вычислить общее сопротивление цепи, изображенной на рисунке.
43. Вычислить площадь трапеции.
Процедуры ввода-вывода
44. Напишите программу, которая изобразила бы на экране большими (во весь экран) буквами некоторое слово, при этом каждая большая буква слова должна быть составлена (как из мозаики) из соответствующих маленьких букв:
| a) SIN | b) COS | c) ABS | d) LOG | e) EXP | f) SQR | g) MOD | h) DIV | i) VAR | j) END |
| k) FOR | l) DOS | m) INC | n) DEC | o) ARC | p) ASM | q) AND | r) NOT | s) API | t) BAR |
| u) RED | v) IDE | w) CGA | x) EGA | y) VGA | z) CHR |
45. Записать оператор, который вводит с клавиатуры два числа.
46. Записать команду, которая вводит с клавиатуры одно слово и любое число.
47. Записать операторы, которые выдают комментарий: «Введите целое число» вводят значения переменной А.
48. Измените оператор вывода в следующей программе, так чтобы результат печатался на экране в виде
площадь равна... (вместо многоточий должны быть конкретные результаты вычислений).
.........
write(‘Введите длины сторон треугольника’); readln(а, в, с);
p:=(a+b+c)/2;
S:=SQRT(p*(p-а)*(p-в)*(p-с));
writeln(S)
..........
49. Предсказать что появится на экран при выполнении следующих команд:
| а) L:=9;` X:=L*L+4; writeln(L, X); | b) H:=13; P:=19; H:=H+P; writeln(P, H) | c) R:=16; writeln(R); R:=R/8; R:=R+3; Writeln(R) |
50. Определить среднее арифметическое и среднее геометрическое чисел, введенных с клавиатуры.[4]
Оператор ветвления.
51. Составить программу диалога человека с ЭВМ. Машина задает вопросы, на которые возможны ответы типа ДА/НЕТ. В зависимости от полученного ответа задает тот или иной следующий вопрос. Предусмотреть в программе не менее трех вопросов машины. Тема диалога:
| a) о проведении свободного времени; | b) о компьютере; |
| c) о природе; | d) о зиме; |
| e) о лете; | f) о погоде; |
| g) о животном мире; | h) о твоем доме; |
| i) о прочитанной книге; | j) о весне; |
| k) об осени; | l) об учебе; |
| m) о театре; | n) о программировании. |
52. Определить, является ли треугольник, заданный тремя сторонами, прямоугольным.
53. Составить программу вычисления значения функции. Исполнить ее при заданных значениях переменной:
a)  ; x=0,75; x=2; x=-2; ; x=0,75; x=2; x=-2;
| b) 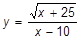 ; x=-13; x=10,67; x=15,53; ; x=-13; x=10,67; x=15,53;
|
c) 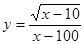 ; x=-126,95; x=100; x=1,03; ; x=-126,95; x=100; x=1,03;
| d) 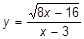 ; x=1; x=3; x=3,85; ; x=1; x=3; x=3,85;
|
e)  [5] x=4,15; x=3; x=13,45; [5] x=4,15; x=3; x=13,45;
| f)  ; x=9; x=-9; x=1,78; ; x=9; x=-9; x=1,78;
|
g) 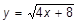 ; x=-2; x=-3; x=0,7; ; x=-2; x=-3; x=0,7;
| h) y = ln(x+1); x=-1; x=1,7; x=-2. |
i) 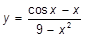 ; x=3; x=-3; x=10,82; ; x=3; x=-3; x=10,82;
| j) 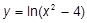 ; x=2; x=1; x=-1; ; x=2; x=1; x=-1;
|
k) 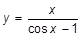 ; x=1; x=-1; x=0,6; ; x=1; x=-1; x=0,6;
| l)  ; x=0,5; x=0; x=1,39; ; x=0,5; x=0; x=1,39;
|
m) 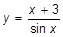 ; x=0; x=-3; x=0,78; ; x=0; x=-3; x=0,78;
| n) 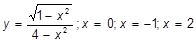
|
o) 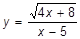 ; x=-2; x=-2.5; x=5 ; x=-2; x=-2.5; x=5
|
54. Точка задана своими координатами x, y. Определить в какой четверти координатной плоскости она лежит.
55. Составить программу решения уравнения 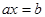 .
.
56. Определить, является ли треугольник, заданный двумя сторонами и углом между ними, равнобедренным.
57. Определить является ли треугольник, заданный тремя сторонами, равносторонним.
58. Определить, лежат ли две точки, заданные своими координатами на одной окружности с центром в начале координат.
59. Заданы площади круга R и квадрата S. Определить:
| a) поместится ли квадрат в круге; | b) поместится ли круг в квадрате |
60. В ЭВМ поступают результаты соревнований по плаванию для трех спортсменов. Выбрать и напечатать лучший результат.
61. Даны три числа A, B, C. Определить:
| a) есть ли среди них равные числа; | b) какое из них большее; |
| c) есть ли среди этих чисел отрицательное число. | d) если среди них положительные числа. |
| e) сколько среди них отрицательных; |
62. Задается число x. Вычислить модуль числа, не использую функцию abs.
63. Записать команду перераспределения значений переменных x и y, так чтобы в x оказалось большее из этих значений, а в y — меньшее.
64. Записать следующее действие в виде одного оператора:
| a) d = max(a, b); | b) 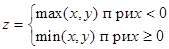
|
c) 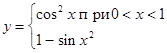
| d) 
|
65. Какое значение будет иметь переменная z после выполнения операторов
z:=0;
IF x>0 THEN IF y>0 THEN z=1 ELSE z=2
при следующих значениях x и y:
| a) x=y=1; | b) x=1, y=1; | c) x=-1, y=1. |
66. Если значение переменной w не равно 0, тогда поменять знак у w, а если значение w равно 0, тогда присвоить w значение 1.
67. Напишите программу вычисления значений функции y=f(x),
где f(x) задана графиком:
| y |
|
| x |
|
68. Написать программу для вычисления значений функции, график которой приведен на рисунке:
69. Написать программу для вычисления значений функции, график которой изображен на рисунке:
|

|
70. a) Даны действительные числа x и y. Если можно, то вычислить ln(x-y).
b) Даны действительные числа x и y. Если можно, то вычислить x/y.
c)Даны действительные числа x и y. Если можно, то вычислить tg(5+y)/(x+y).
d) Даны действительные числа x и y. Вычислить

71. Даны действительные числа a и b. Проверить, выполняются ли неравенства a>b>10.
72. Даны действительные числа а, b, c. Проверить, выполняются ли неравенства a<b<c.
73. Даны два действительных числа. Заменить первое число нулем, если оно меньше или равно второму, в противном случае числа оставить без изменения.
74. Даны три действительных числа. Выбрать из них те, которые принадлежат отрезку
[2, 4].
75. С клавиатуры вводятся две оценки. Напишите программу, которая выведет на экран “Молодец” если их сумма больше или равна девяти.
76. Проверить делится ли число a на число b без остатка.
77. Даны действительные числа x и y. Меньшее из этих чисел заменить их полусуммой, а большее — их утроенным произведением.
78. Даны действительные числа x, y, z. Получить:
a) min(x, y, z);
b) min(x, y, z) и max(x, y, z);
c) 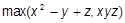 .
.
d) 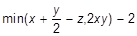 .
.
79. Дано: действительные числа a и b. Вычислить f(a)+f(b), если
a) 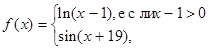 ;
;
b) 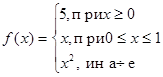 .
.
80. Даны действительные числа x и y. Если х и y отрицательны, то каждое их значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0.5; если оба значения неотрицательны и ни одно из них не принадлежит отрезку [0.5; 2], то оба значения уменьшить в 10 раз; в остальных случаях x и y оставить без изменения.
81. Даны действительные числа a, b, c, x, y. Проверить, принадлежит ли точка М(x, y) прямой l с уравнением ax+by+c =0.
82. Даны действительные положительные числа x, y, z. Выяснить, существует ли треугольник со сторонами x, y, z.
83. Даны действительные числа a, b, c. Полностью исследовать биквадратное уравнение 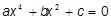 , т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
, т.е. если действительных корней нет, то должно быть выдано сообщение об этом, иначе должны быть выданы два или четыре корня.
84. Даны действительные числа a, b, c, d. Если 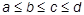 , то каждое число заменить наибольшим из них; если а>b>c>d, то числа оставить без изменения; в остальных случаях все числа заменить их квадратами.
, то каждое число заменить наибольшим из них; если а>b>c>d, то числа оставить без изменения; в остальных случаях все числа заменить их квадратами.
|
| y |
85. Дано действительное число a. Для f (x), график которой представлен на рисунке 1, вычислить f (a - 2).
| x |
| рис. 1 |
86. Даны действительные числа x и y. Определить, принадлежит ли точка с координатами x, y заштрихованной части плоскости (см. рис. 2 a) и б)).
          
|
|
| y |
| x |
| рис. 2. a) |
| рис. 2. б) |
87. Дано не менее трех различных натуральных чисел, за которыми следует 0. Определить три наибольших из них.
88. Составьте программу нахождения произведения двух наибольших из трех чисел.
89. Составить программу вычисления функции.
a) 
| b) 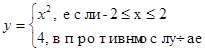
|
c) 
| d) 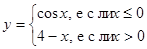
|
e) 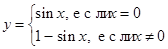
| f) 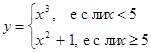
|
g) 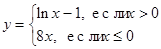
| h) 
|
i) 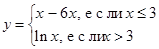
| j) 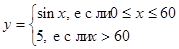
|
k) 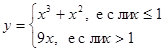
| l) 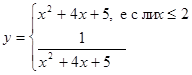
|
m) 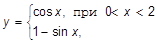
| n) 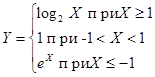 [6] [6]
|
90. Даны три числа. Если они могут быть длинами некоторого треугольника, выяснить: является ли этот треугольник остроугольным.
91. Размеры прямоугольного окна A и B. Размеры шкафа, имеющего форму прямоугольного параллелепипеда — C, D, E. Определить, пройдет ли шкаф в окно.
92. Вычислить 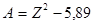 , если
, если 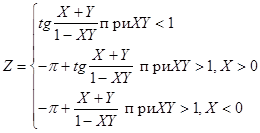
93. Вычислить 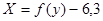 , если
, если 
94. Даны два числа X и Y. При  ; иначе
; иначе  . Вычислить P.
. Вычислить P.
95. Вычислить 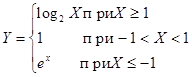 .
.
96. Что больше 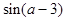 или
или  ?
?
97. Что больше  или
или 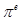 ?
?
98. Даны названия трех месяцев. Определить, к какому времени года они относятся.
Операторы цикла
99. За создание шахмат их изобретатель попросил такую награду: за первую клетку шахматной доски — 1 зерно; за вторую — 2; за третью — 4 и т. д. Т.е. за каждую последующую в два раза больше, чем за предыдущую. Напишите программу для подсчета количества зерен, причитающихся ему. Определите это количество.
100. Тело брошено вертикально вверх со скоростью V. Напишите программу для составления таблицы его положений с шагом dt.
101. Тело брошено под углом a к горизонту с начальной скоростью V. Составьте таблицу положений тела вдоль оси 0X через промежутки времени dt.
102. Тело брошено под углом a к горизонту с начальной скоростью V. Составьте таблицу положений тела вдоль оси 0Y через промежутки времени dt.
103. Существует ли целое число, квадрат которого расположен между числами 12345 и 54321?
104. Известно, что sin(x) можно вычислить по формуле:
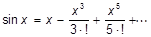
Напишите программу для вычисления по это формуле с учетом всех членов не меньших по модулю некоторого малого положительного числа е.
105. Известно, что cos(x) можно вычислить по формуле:
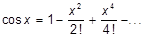
Напишите программу для вычисления по это формуле с учетом всех членов не меньших по модулю некоторого малого положительного числа e.
106. Один чудак предложил одному миллионеру такую сделку: он (чудак) в течение 30 дней приносит миллионеру по 100000 $. Взамен миллионер платит в первый день 1 цент, во второй - 2; в третий - 4 и т. д. Напишите программу для определения того, сколько же заработает на этой сделке миллионер.
107. Зная рост человек L, можно определить его оптимальный вес P по формуле:

Составьте таблицу зависимости веса от роста в пределах 150 — 200 см. с шагом 2.5 см.
108. Один любящий муж, живущий в двух милях от работы, отправившись утром на службу и пройдя 1 милю вспомнил, что забыл поцеловать жену. Тогда он решил вернуться, но пройдя 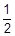 мили, изменил свое решение и повернул на работу. Когда он прошел еще
мили, изменил свое решение и повернул на работу. Когда он прошел еще  мили, он снова решил вернуться домой, но пройдя еще
мили, он снова решил вернуться домой, но пройдя еще  мили опять изменил свое решение и т. д. и т. п. Напишите программу и определите на каком расстоянии от дома он окажется через 10 таких смен настроения.
мили опять изменил свое решение и т. д. и т. п. Напишите программу и определите на каком расстоянии от дома он окажется через 10 таких смен настроения.
109. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивает дневную норму на 10% от нормы предыдущего дня. Какой путь пробежит спортсмен на n-й день?
110. Составить программу для вычисления частичной суммы ряда:
a) 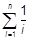 ; ;
| b) 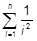 ; ;
| |
c) 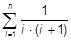 ; ;
| d)  ; ;
| |
e) 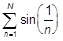
| f) 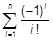
| |
g) 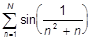
| h) 
| |
i) 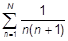
| j) 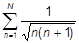 ; ;
| |
k)  ; ;
| l) 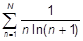 ; ;
| |
m) 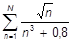 ; ;
| n) 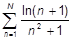 ; ;
| |
o) 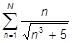 ; ;
| p) 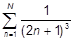 ; ;
| |
q); 
| r) 
| |
s) 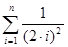 u)
u) 
| t) 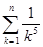 v)
v) 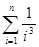
| |
w) 
| x) 
| |
y) 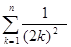
| ||
z) 
| ||
111. Написать программу для вычисления произведения:
a) 
| b) 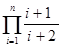
|
c) 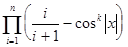
| d) 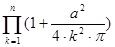
|
112. Напишите программу для вычисления суммы вида:
a) 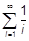 ; ;
| b) 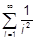 ; ;
|
c) 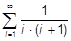 ; ;
| d) 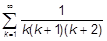 ; ;
|
e) 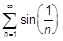
| f) 
|
g) 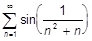
| h) 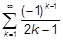
|
i) 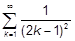
| j) 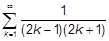
|
k) 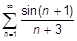
| l) 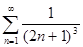
|
m) 
| n) 
|
с учетом всех членов неменьших по модулю некоторого малого положительного числа e.
113. Кузнечик стремится выскочить из круга радиусом 1 м., в центре которого он находится. Первый прыжок он совершает на 0.5 м., второй на 0.25 м. и т. д. Напишите программу для определения расстояния пропрыганного кузнечиком. На каком прыжке он выскочит из круга?
114. В 1699 г. математик Шарп показал, что

Напишите программу для приближенного вычисления p по этой формуле. Вычислите p с использованием n членов.
115. Вычислить и записать n членов последовательности:
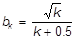
116. Оказывается, что корень кубический из числа x может быть вычислен по формуле:
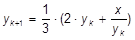
где x — число из которого извлекается корень,  — очередное приближение к корню кубическому из этого числа. Напишите программу для вычислений по этой формуле. (Приближения следует прекратить, когда модуль разности между
— очередное приближение к корню кубическому из этого числа. Напишите программу для вычислений по этой формуле. (Приближения следует прекратить, когда модуль разности между  и
и 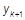 окажется меньше некоторого малого заданного числа e.)
окажется меньше некоторого малого заданного числа e.)
117. Напишите программу для определения среднего роста n человек.
118. Иногда уравнения вида x=f (x) можно решать следующим образом:

где  — очередное приближение к точному значению корня. Процесс вычислений прекращают тогда, когда разница между соседними приближениями окажется меньше некоторого малого числа e. Напишите программу для решения таким образом уравнения:
— очередное приближение к точному значению корня. Процесс вычислений прекращают тогда, когда разница между соседними приближениями окажется меньше некоторого малого числа e. Напишите программу для решения таким образом уравнения:
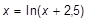
(В качестве начального значения x можно взять любое число).
119. Написать программу для вычисления следующей суммы:
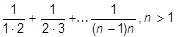
120. «Новое» налоговое законодательство устанавливает следующие ставки налогов в пределах от 150 до 700 руб. дохода: 14.7 руб. + 13% от суммы, превышающей 150 руб. Составьте программу для вычисления суммы налога с заработка от 150 до 700 руб. с шагом 10 руб.
121. «Новое» налоговое законодательство устанавливает следующие ставки налогов на разовые заработки в пределах от 701 до 900 руб. в месяц: 86.2 + 15% от суммы, превышающей 700 руб. Напишите программу для составления таблицы чистого (без налога) заработка в пределах от 701 до 900 руб. с шагом 10 руб.
122. «Новое» налоговое законодательство устанавливает следующие ставки налогов на разовые заработки в пределах от 1501 до 3000 руб. в месяц: 296.2+50% от суммы, превышающей 1500 руб. Напишите программу для составления таблицы чистого (без налога) заработка в пределах от 1501 до 3000 руб. с шагом 10 руб.
123. На доходы индивидуалов установлена (была) следующая налоговая ставка: при годовом доходе от 3001 до 4000 руб. 332.1 руб. + 20% с суммы превышающей 3000. Напишите программу для составления таблицы чистого дохода (без налогов) в пределах от 3001 до 4000 руб. с шагом 10 руб.
124. По мнению некоторых экономистов темпы инфляции рубля в «настоящее» время составляют 7.7% в месяц, т.е. за месяц рубль теряет 7.7% своей стоимости. Напишите программу для определения реальной стоимости рубля через n лет. Определите через, сколько лет рубль (при таких темпах инфляции) будет стоить 10 копеек.
125. Сберегательная касса начисляет 120% годовых, т.е. через год вклад увеличивается без участия вкладчика. Какой станет сумма k рублей, положенная в кассу на n лет?
126. Каждая бактерия делится на две через 1 минуту. В начальный момент имеется 1 бактерия. Сколько их будет через n минут?
127. Амеба делится каждые 3 часа на 2 клетки. Определить, сколько клеток будет через 3, 6, 9, 12, …, 24 часа.
128. Напечатать значения первых n членов арифметической прогрессии.
129. Напечатать n первых членов геометрической прогрессии.
130. Вычислить 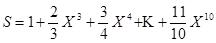 .
.
131. Написать программу для вычисления произведения:
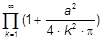
принимая во внимание лишь члены не меньшие некоторого малого числа  .
.
132. Напишите программу для вычисления суммы всех натуральных чисел от 1 до n.
133. Написать программу для вычисления следующей суммы:
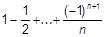
134. Написать программу для вычисления следующего произведения:
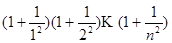
135. Напишите программу для вычисления по формуле:

Вычислите при n=10.
136. Дано действительное число a. Найти среди чисел 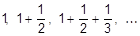 первое большее a.
первое большее a.
137. Дано действительное число a. Среди чисел 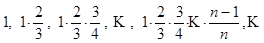 найти первое большее a.
найти первое большее a.
138. Дано действительное число a. Найти такое наименьшее n, что 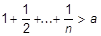 .
.
139. Дано число e. Среди чисел

найти первое такое, что 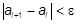
140. Вычислите:
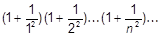
с точностью e, т.е. учитывая только те члены которые не меньше чем e.
141. 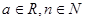 . Вычислить
. Вычислить  .
.
142. Строим некоторую кривую, заданную формулой:
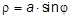
где r — расстояние до данной точки от начала координат, j — угол между направлением на эту точку и осью OX. Напишите программу для составления таблицы этой функции, j меняется от 0 до 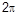 с шагом h.
с шагом h.
143. Вы взяли в банке ссуду под 60% годовых. Напишите программу для определения Вашего долга банку через n лет. Вычислите, сколько Вам придется вернуть в банк, если Вы взяли 1000 рублей, а возвращаете ссуду через 10 лет.
144. Верно ли что:

Напишите программу для вычислений и проверьте при различных n.[7]
145. Построить таблицу значений функции
a) 
| b) 
|
c) 
| d) 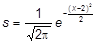
|
e) 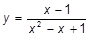 ; ;
| f)  ; ;
|
g)  ; ;
| h) 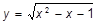 ; ;
|
i) 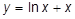 ; ;
| j) 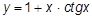 ; ;
|
k) 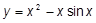 ; ;
| l) 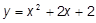 ; ;
|
m) 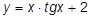 ; ;
| n) 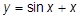 ; ;
|
o) 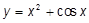 ; ;
| p) 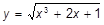 ; ;
|
q) 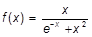 ; ;
| r) 
|
s) 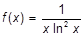
| t) 
|
u) 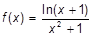 ; ;
| v)  ; ;
|
w) 
|
на некотором отрезке [А, В] с некоторым шагом Н.[8]
146. Вычислить произведение первых n натуральных чисел.
147. Составить таблицу умножения для числа 12.
148. Дано натуральное число n. Вычислить:
a) 1+2+...+n;
b) 1+1/2+...+1/n;
c) 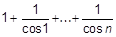 ;
;
d) sin(n-3) + sin(n-6) +... + sin(n-60);
e)  ;
;
f) n!;
g) 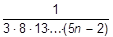 ;
;
h) 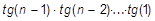 ;
;
i) 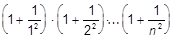 ;
;
j) 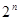 .
.
149. Вычислить 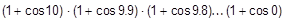 .
.
150. Даны действительное число a, натуральное число n. Вычислить:
a)  ;
;
b) 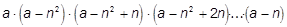 .
.
151. Дано действительное число х. Вычислить:
a) 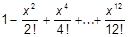 .
.
b) 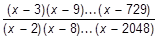
152. Дано действительное число х, натуральное число n. Вычислить:
a) 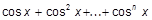 ;
;
b)  ;
;
c) 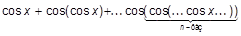 ;
;
d) 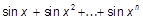 .
.
153. Дано натуральное число n. Вычислить  .
.
154. Вычислить 
155. Вычислить 
156. Дано действительное число х. Вычислить 
157. Дано натуральное число n. Вычислить произведение первых n сомножителей вида:
a)  ;
;
b) 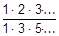 .
.
158. Ввести с клавиатуры n чисел. Найти:
a) их сумму;
b) их произведение;
c) среди них максимальное и минимальное числа.
159. Пусть 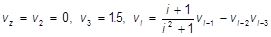 , для i =4… Найти
, для i =4… Найти  .
.
160. Пусть 

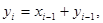
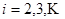 .Найти
.Найти 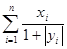 .
.
161. 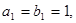


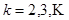 . Найти
. Найти 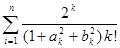 .
.
162. 

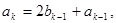

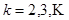 . Найти
. Найти 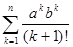 .
.
163. Оценить[9] 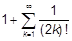 . Сравнить с chx[10].
. Сравнить с chx[10].
164. Оценить 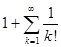 . Сравнить с
. Сравнить с 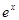 .
.
165. Оценить 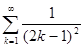 . Сравнить с
. Сравнить с  .
.
166. Оценить 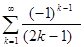 . Сравнить с
. Сравнить с 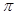 .
.
167. Вычислить бесконечную сумму с заданной точностью e (e>0). Считать, то требуемая точность достигнута, если очередное слагаемое оказалось по модулю меньше, чем e, — это и все последующие слагаемые можно уже не учитывать:
a) 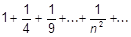 ;
;
b) 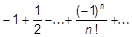 ;
;
c)  .
.
168. Даны действительные числа x, e ( , e>0). Вычислить с точностью e:
, e>0). Вычислить с точностью e:
a) 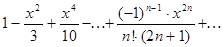 ;
;
b)  .
.
169. Даны действительные числа x, a, e (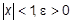 ). Вычислить с точностью e значение
). Вычислить с точностью e значение
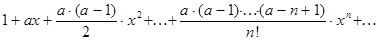
170. Даны действительные числа x, e (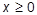 , e>0). Вычислить с точностью e бесконечную сумму и указать количество учтенных слагаемых:
, e>0). Вычислить с точностью e бесконечную сумму и указать количество учтенных слагаемых:
a)  ;
;
b) 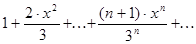 .
.
171. Дано действительное число. Последовательность а (1), а (2),... образована по следующему закону:

Получить сумму k слагаемых, где k — наименьшее целое число, удовлетворяющее двум условиям: k > 10 и 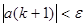 .
.
172. Дано действительное число. Последовательность а (1), а (2),... образована по следующему закону:
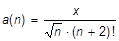
Получить сумму k слагаемых, где k — наименьшее целое число, удовлетворяющее двум условиям: k > 10 и 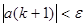 .
.
173. a) Дано действительное число e (e>0). Последовательность а (1), а (2),... образована по следующему закону:
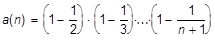
Найти первый член последовательности a (k) (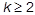 ), для которого выполнено условие
), для которого выполнено условие 
b) Дано действительное число e (e>0). Последовательность а (1), а (2),... образована по следующему закону:

Найти первый член последовательности a (k) (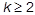 ), для которого выполнено условие
), для которого выполнено условие 
174. Дано натуральное число n. Вычислить 1*2 + 2*3 +... + n*(n+1)*... *2n.
175. Пусть n — натуральное число и пусть n!! означает 1*3*5*...*n для нечетного n и 2*4*... *n для четного n. Для заданного n вычислить:
a) n!!;
b) 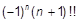 .
.
176. Вычислить:
a) 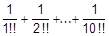 ;
;
b)  .
.
177. Дано малое положительное число e. Вычислить бесконечную сумму с заданной точностью e. Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем e, — это и все последующие слагаемые можно не учитывать. Вычислить:
a) 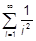 ;
;
b) 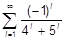 .
.
178. 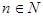 . Вычислить
. Вычислить 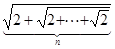 .
.
179. 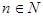 . Вычислить
. Вычислить 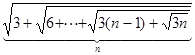 .
.
180. 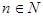 ,
, 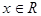 . Вычислить
. Вычислить 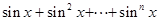 .
.
181. Вычислить 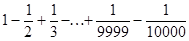 .
.
182. То же, что и задание 181, но сначала найти сумму положительных членов, потом — отрицательных, и, наконец, всю сумму. Сравните с результатом полученным в предыдущем задании.
183. То же, что и задание 181, но сначала найти сумму отрицательных членов, потом — положительных, и, наконец, всю сумму. Сравните с результатом полученным в задании №181.
184. 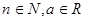 . Вычислить
. Вычислить 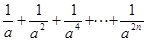
185. Найти номер и значение первого меньшего нуля, тангенса, среди:  .
.
186. Найти сумму 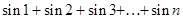 до первого отрицательного слагаемого.
до первого отрицательного слагаемого.
187. Найти среднее арифметическое расстояний от точки (0, 0) до точек графика функции 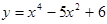 с абсциссами 1, 2, …, k.
с абсциссами 1, 2, …, k.
188. Найти среднее арифметическое значений функции 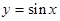 для x=1, 2, …, n
для x=1, 2, …, n