| Условия расчета | Формула расчета |
| Средний уровень ряда для интервальных рядов |  или  
|
| Средний уровень для моментных рядов с неравными промежутками между периодами |  ;где yi – i-тый уровень ряда динамики; ti- время, в течение которого i-тый уровень остается неизменным
|
| Средний уровень ряда для моментных рядов с равными промежутками между моментами | Средняя хронологическая
|
| Средний темп роста |  К2К3….Кn-1
|
| Средний абсолютный прирост |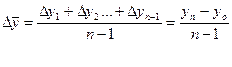 
Где: 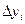 - цепные абсолютные приросты;
n- число уровней ряда динамики
|
Виды зависимостей, используемых при аналитическом выравнивании рядов динамики
| Виды зависимости и формула | Условия применения зависимости |
Линейная
| Выбирается при более или менее постоянных цепных приростах |
Параболическая
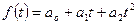
| Выбирается при постоянном темпе прироста |
Гиперболическая
| Выбирается при постоянном отрицательном темпе прироста |
Тема Корреляция (задача 7)
Формулы для расчета параметров уравнения и показателей тесноты связи (корреляция)
| Вид связи по аналитическому выражению | |
| прямолинейная | Выражается уравнением прямой: У=а0+ а1Х Для нахождения параметров ао и а1 применяют метод наименьших квадратов и решают систему из двух уравнений:
|
| параболическая | Выражается уравнением параболы у=ао+а1х +а2х2. Для нахождения параметров уравнения решают систему из трех уравнений:
|
| гиперболическая | Выражается уравнением гиперболы: у= ао+  . Параметры находят с помощью системы двух уравнений:
|
| Показатели тесноты связи | |
| Эмпирическое (фактическое) корреляционное отношение |  ;  -межгрупповая дисперсия (дисперсия групповых средних) значений результативного признака, рассчитанных по уравнению регрессии;
 - общая дисперсия.
Рассчитывается по данным группировки, когда характеризует отклонение групповых средних результативного показателя от общей средней. Применяется для характеристики тесноты связи для всех форм связи
|
| Теоретическое корреляционное отношение | 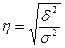 ;  -дисперсия значений результативного признака, рассчитанных по уравнению регрессии;
- дисперсия фактических значений результативного признака
Применяется для характеристики тесноты связи для всех форм связи
|
| Коэффициент корреляции |  ;  -среднее произведений факторного и результативного признака;  - среднее значение факторного признака;  среднее значение результативного признака;  и  - среднеквадратичное отклонение, соответственно, признака «х» и признака «у». Применяется для характеристики тесноты связи при линейной зависимости
|
