Лабораторная работа №4
Переменная 
(с областью изменения Z) называется функцией независимых переменных 
в множестве М, если каждой паре 
их значений из М по некоторому правилу или закону ставится в соответствие одно определенное значение из множества Z.
Множество М – область определения функции, множество Z – область ее значений. Функциональная зависимость от обозначается так: 
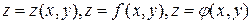и т.п.
Возьмем в пространстве систему координатных осей 
, изобразим на плоскости 
множество М; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение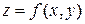 
.
Геометрическое место полученных таким образом точек и является пространственным графиком функции .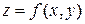
Фрагмент рабочего документа Mathcad с графиками функций 
приведен ниже.
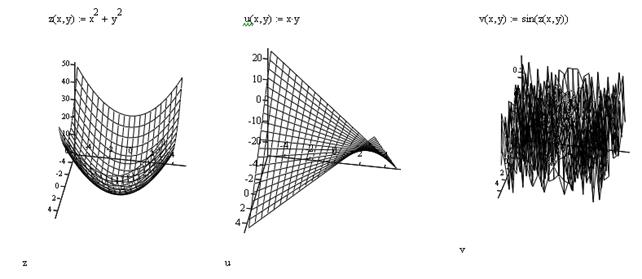
Указание: Для того чтобы построить в Mathcad график функции двух переменных, щелкните в панели 
на кнопке 
, введите в помеченной позиции имя z и щелкните по рабочему документу вне поля графиков.
Линией уровня функции двух переменных 
и 
называется геометрическое место точек в плоскости , в которых функция принимает одно и то же значение. Линии уровня функции 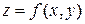определяются уравнением 
, где 
.
Рассматривая линии уровня функции двух переменных, можно исследовать характер изменения функции, найти (приближенно, но как угодно точно) координаты точек экстремума. Ниже приведены линии уровня функций, графики которых изображены выше.
Рис. 1. Линии уровня функций двух переменных
Указание: Линии уровня можно построить, щелкнув в панели графиков по кнопке 
. В данном случае использован другой способ – линии уровня получены изменением параметров настройки графиков. На рис. 2 изображены панели настройки параметров линий уровня для каждого из графиков, приведенных на рис. 1.
Рис. 2. Панели настройки параметров изображений линий уровня
Точка 
называется точкой локального минимума (максимума) функции 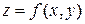, определенной в области 
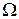, если существует такая проколотая окрестность 
, что для всех точек 
справедливо неравенство 
.
Ниже приведен фрагмент рабочего документа Mathcad с построением графика функции 
в области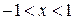 
, 
.
Рис. 3
Из графика видно, что функция имеет локальные минимумы и локальные максимумы.
На рис. 4 слева изображены линии уровня без числовой индикации, справа – на каждой линии уровня написано соответствующее значение функции. Видно, что в изображенной области функция имеет два локальных минимума (во втором и четвертом квадрантах), координаты точек локального минимума можно определить приближенно (это точки 
и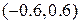 
, и две точки локального максимума (в первом и третьем квадрантах) – это точки 
и 
. Точка 
- седловая точка. Поведение функции в окрестности этой точки близко к поведению функции 
, график которой – гиперболический параболоид – называют «седлом».
Рис. 4. Линии уровня графика функции
Задание 1
Изобразите график и линии уровня функции 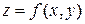в указанном прямоугольнике 
. Опишите поведение функции в заданной области (укажите приближенно координаты локальных экстремумов и седловых точек, если они есть).
