Целевая функция:

Ограничения:
а) по строкам:

б) по столбцам:

Балансовое условие:

Условие неотрицательности переменных:

Таблица 8
Табличное представление исходных данных задачи
| № п/п | Культуры | Урожайности культур по участкам (ц.к.е./га) | Площадь посева, га | |||
| I | II | III | IV | |||
| Кукуруза на силос | X11 | X12 | X13 | X14 | ||
| Одн.травы на з/к | X21 | X22 | X23 | X24 | ||
| Одн. травы на сено | X31 | X32 | X33 | X34 | ||
| Картофель | X41 | X42 | X43 | X44 | ||
| Горох | 18 X51 | X52 | X53 | X54 | ||
| Мн. травы на сено | X61 | X62 | X63 | X64 | ||

| Площади участков, га |
Проверка сбалансированности задачи
 что не равно
что не равно  , задача несбалансирована, причем
, задача несбалансирована, причем 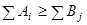 . Чтобы привести задачу к сбалансированному виду, вводим фиктивный участок с площадью, равной
. Чтобы привести задачу к сбалансированному виду, вводим фиктивный участок с площадью, равной  896. Чтобы значение целевой функции не изменилось, урожайность по фиктивному участку примем равными нулю Сi5=0, i=1,2,3,4,5,6. В результате исходная таблица примет вид табл.9.
896. Чтобы значение целевой функции не изменилось, урожайность по фиктивному участку примем равными нулю Сi5=0, i=1,2,3,4,5,6. В результате исходная таблица примет вид табл.9.
Таблица 9
Приведение задачи к сбалансированному виду с помощью фиктивных объектов (строки или столбца)
| № п/п | Культуры | Урожайности культур по участкам (ц.к.е./га) | Площадь посева, га | ||||
| I | II | III | IV | V(ф) | |||
| Кукуруза на силос | X11 | X12 | X13 | X14 | X15 | ||
| Одн.травы на з/к | X21 | X22 | X23 | X24 | X25 | ||
| Одн. травы на сено | X31 | X32 | X33 | X34 | X35 | ||
| Картофель | X41 | X42 | X43 | X44 | X45 | ||
| Горох | 18 X51 | X52 | X53 | X54 | X55 | ||
| Мн. травы на сено | X61 | X62 | X63 | X64 | X65 | ||

| Площади участков, га |
Учет дополнительных ограничений
1) дополнительное ограничение типа 
 , для выполнения этого условия
, для выполнения этого условия  и
и  должны быть уменьшены на 550. Определяем измененные значения
должны быть уменьшены на 550. Определяем измененные значения  A3 и B3:
A3 и B3:
A3/=A3-550=1100-550=550
B3/=B3-550=2600-550=2050
2) дополнительное ограничение типа 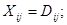
 определяем измененные значения A2 и B4
определяем измененные значения A2 и B4
A2/=A2-300=2300-300=2000
B4/=B4-300=1554-300=1254;
дополнительно изменяем оценку С24, проводим блокировку оценки, придаем ей невыгодное значение, при решении на максимум – минимальное значение, т.е. С24=0.
 , аналогично, уменьшаем A4 и B4 на 990, тогда
, аналогично, уменьшаем A4 и B4 на 990, тогда
A4/=950-950=0, соответствующая строка 4 вычеркивается из исходной матрицы, а нумерация строк сохраняется при дальнейшем решении задачи.
B4//=1254-950=304.
3) дополнительное ограничение типа 
 ,
,
данное ограничение учитывается после получения оптимального решения.
В результате учета дополнительных условий получим следующую таблицу (табл.10).
Таблица 10
Табличное представление исходных данных задачи после учета дополнительных условий и требования сбалансированности
| j i | Ai | |||||
 Bj Bj
|
Граничные условия
Развернутая запись
а) по строкам исходной матрицы:
X11+X12+X13+X14+X15=1400
X21+X22+X23+X24+X25=2000
X31+X32+X33+X34+X35=550
X51+X52+X53+X54+X55=2500
X61+X62+X63+X64+X65=800
б) по столбцам исходной матрицы:
X11+X21+X31+X51+X61=2100
X12+X22+X32+X52+X62=1900
X13+X23+X33+X53+X63=2050
X14+X24+X34+X54+X64=304
X15+X25+X35+X55+X65=896
в) балансовое условие:  , после проведенных преобразований оно автоматически выполняется.
, после проведенных преобразований оно автоматически выполняется.
г) условие неотрицательности переменных:
 .
.
Целевая функция задачи:

Необходимо найти такой план распределения посевов кормовых культур по участкам различного плодородия, т.е. такие значения величин  (i=1,2,3,5,6; j=1,2,3,4,5), чтобы сбор кормов был максимальным.
(i=1,2,3,5,6; j=1,2,3,4,5), чтобы сбор кормов был максимальным.
Таблица 11
Получение опорного решения методом аппроксимации на максимум
 j
i j
i
| Аi | 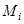
| ||||||||||||
  1 1
| 1300 50 | 41* | ||||||||||||
| 3* | ||||||||||||||
| 26* | 26* | |||||||||||||
  5 5
| 2196 896 | 3* | ||||||||||||
| *1 | ||||||||||||||
     Bj Bj
| ||||||||||||||

| ||||||||||||||
| 2* | ||||||||||||||
| 1* | ||||||||||||||
| 15* | ||||||||||||||
Проверка опорного решения на выполнение граничных условий.
а) по строкам:
1. 100+50+1250=1400
2. 2000 =2000
3. 550 =550
5. 1300+304+896=2500
6. 800 =800
б) по столбцам:
1. 100+2000 =2100
2. 50+550+1300=1900
3. 1250+800 =2050
4. 304 =304
5. 896 =896
Проверка на число занятых клеток.
 ;9=9, т.е. решение верное и невырожденное.
;9=9, т.е. решение верное и невырожденное.
Вычисление значения целевой функции.
Zk=  44*100+41*50+42*1250+43*200+26*550+
44*100+41*50+42*1250+43*200+26*550+
+19*1300+22*304+0*896+44*800=225870
Проверка опорного решения на оптимальность: при решении задачи на максимум план оптимален, если для всех свободных клеток  .
.
Вычислим потенциалы. За первый потенциал возьмем 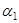 =100, все остальные потенциалы вычисляем по формуле
=100, все остальные потенциалы вычисляем по формуле 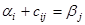 . Для свободных клеток вычисляем оценки
. Для свободных клеток вычисляем оценки  . Результаты расчетов заносим в табл.12.
. Результаты расчетов заносим в табл.12.
Таблица 12
Потенциалы  и оценки
и оценки 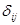 для опорного решения задачи
для опорного решения задачи
| № | 5(ф) | |||||


| ||||||
     1 1
| - | + | ||||
    2 2
| -1 | -43 | -21 | |||
    3 3
| -1 | -7 | ||||
   5 5
| 18 -4 | - | -3 | - | ||
    6 6
| -3 | -3 | -1 | -24 |

Zk=144*2100+141*1900+142*2050+144*304+122*896-
-100*1400+101*2000+115*550+122*2500+98*800=2258358
Улучшение опорного плана
Строим замкнутый прямоугольный цикл с началом в свободной клетке с наибольшей оценкой (испытуемая клетка). Клетка (1,4) с оценкой  =2 не удовлетворяет условию оптимальности. Для нее строим цикл в табл.12. Проставляем знаки «+» и «-», начиная с испытуемой клетки, ищем наименьшее значение хij среди отрицательных вершин. В данном случае хmin=50. Это тот ресурс, который перемещается по циклу и прибавляется или вычитается в зависимости от проставленных знаков в вершинах цикла. Таким образом, получаем новые значения переменных хij, т.е. новое решение задачи. Результаты описанных действий сведем в табл.13.
=2 не удовлетворяет условию оптимальности. Для нее строим цикл в табл.12. Проставляем знаки «+» и «-», начиная с испытуемой клетки, ищем наименьшее значение хij среди отрицательных вершин. В данном случае хmin=50. Это тот ресурс, который перемещается по циклу и прибавляется или вычитается в зависимости от проставленных знаков в вершинах цикла. Таким образом, получаем новые значения переменных хij, т.е. новое решение задачи. Результаты описанных действий сведем в табл.13.
Таблица 13
Улучшенное на 2-м шаге решение задачи
| № | 5(ф) | |||||


| ||||||
     1 1
| -2 | - | + | -24 | ||
    2 2
| -2 | -1 | -45 | -23 | ||
      3 3
| - | + | -7 | |||
   5 5
| -2 | + | -1 | - | ||
    6 6
| -3 | -5 | -3 | -26 |
Полученное решение необходимо проверить на выполнение граничных условий.
а) по строкам:
1. 100+1250+50 =1400
2. 2000 =2000
3. 550 =550
5. 1350+254+896=2500
6. 800 =800
б) по столбцам:
1. 100+2000=2100
2. 550+1350=1900
3. 1250+800=2050
4. 50+254 =304
5.896 =896
Значение целевой функции определяется по формуле:
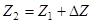 (для задачи на максимизацию должно выполняться условие:
(для задачи на максимизацию должно выполняться условие:  ).
).
 2*50=100, где
2*50=100, где  оценка испытуемой клетки,
оценка испытуемой клетки,  -перемещаемая поставка.
-перемещаемая поставка.
Z2=225838+100=225938
Дополнительно для контроля значение целевой функции рассчитывается по формуле:  44*100+42*1250+46*50+43*2000+26*550+
44*100+42*1250+46*50+43*2000+26*550+
+19*1350+22*254+44*800=221338.
Проверка на оптимальность
Вновь для второго шага вычисляем потенциалы и оценки свободных клеток. Результаты вычислений отразим в табл.13.
В полученной таблице две оценки положительны, значит, требуется дальнейшее улучшение плана. Строим цикл для клетки (3,3).
хmin=254 – ресурс, который будем перемещать по циклу в соответствии с проставленными знаками, в результате получим новые значения переменных, т.е. новое решение, которое представим в табл.14.
Таблица 14
Улучшенное на 3-м шаге решение задачи
| № | 5(ф) | |||||


| ||||||
  1 1
| -22 | |||||
    2 2
| -1 | -45 | -21 | |||
   3 3
| -1 | -2 | -7 | |||
   5 5
| -4 | -3 | -2 | |||
   6 6
| -3 | -3 | -3 |






