Тема 1.2 Геометрические построения
Построение прямых углов. Угол 90 целесообразно строить при помощи рейсшины и угольника (рис. 53).
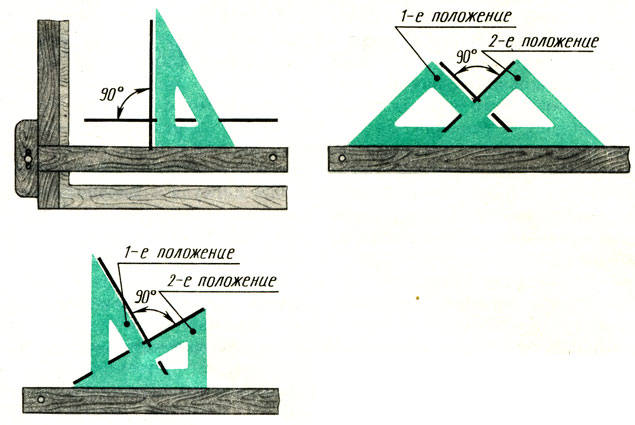
Рис. 53. Построение прямых углов
Построение тупых и острых углов. Рациональные способы построения углов 120, 30 и 150; 60 и 120; 15 и 165; 75 и 105; 45 и 135 приведены на рис. 54.
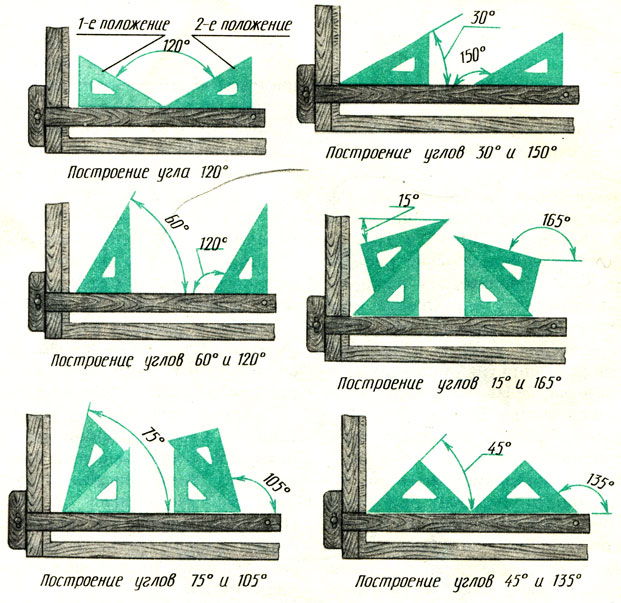
Рис. 54. Построение тупых и острых углов
Деление угла пополам. Из вершины угла описывают дугу окружности произвольного радиуса (рис. 55). Из точек m и n пересечения дуги со сторонами угла раствором циркуля, большим половины дуги mn, делают две пересекающиеся засечки (точка 1).
Полученную точку 1 соединяют прямой с вершиной угла.
Рис. 55.
Деление отрезка прямой пополам. Из концов заданного отрезка раствором циркуля, большим половины его длины, описывают дуги (рис. 56). Прямая, соединяющая полученные точки m и n, делит отрезок на две равные части и перпендикулярна ему.
Рис. 56.
Деление прямого угла на три равные части. Из вершины прямого угла описывают дугу окружности произвольного радиуса (рис. 57). Не меняя раствора циркуля, делают засечки из точек пересечения дуги со сторонами угла. Полученные точки тип соединяют прямыми с вершиной угла.
Рис. 57.
Деление окружности на три равные части. Угольник с углами 30 и 60 устанавливают так, чтобы большой катет был параллелен одной из центровых линий. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду, получают второе деление (рис. 58, а). Перевернув угольник и проведя вторую хорду, получают третье деление (рис. 58, б). Соединив точки 2 и 3 прямой, получают равносторонний треугольник.
Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в конечную точку диаметра (рис. 58, в), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление (точки 1 и 2). Третье деление (точка 3) находится на противоположном конце диаметра.
Рис. 58.
Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности (рис.
(В книге-источнике отсутствуют страницы: 49-50)
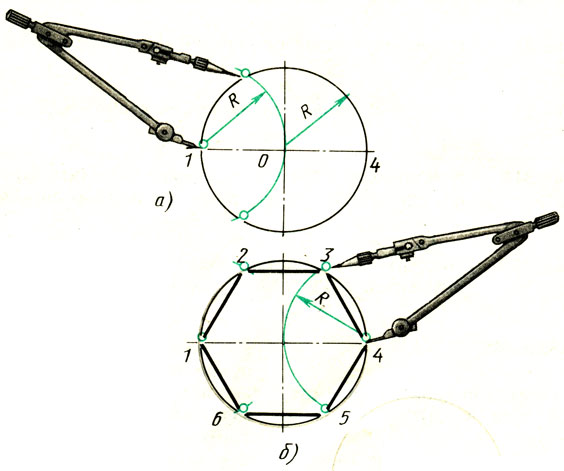
Рис. 59. Деление окружности на шесть равных частей при помощи циркуля
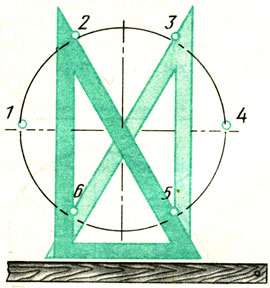
Рис. 60. Деление окружности на шесть равных частей при помощи угольника
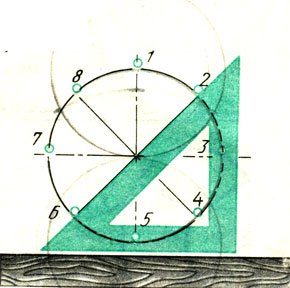
Рис. 61. Деление окружности на восемь равных частей
Рис. 62. Определение центра дуги
Рис. 3
Деление окружности на семь равных частей (рис. 3) выполняется в следующей последовательности:
1. Начертить окружность радиуса R30. Проведите два взаимноперпендикулярных диаметра. При пересечении окружности и горизонтального диаметра отметьте точку 1.
2. Из точки 1 радиусом, равным радиусу окружности R30, проводим дугу, которая пересечет окружность в точке А и А/.
3. Соединяем точки А и А/.
4. При пересечении прямой АА/ и горизонтального диаметра отметим точку В.
5. Расстояние АВ откладываем от точки 1 по окружности семь раз и получают искомые точки 1 – 7.
Сопряжения. У шаблона на рисунке 130 углы скруглены. Прямые линии плавно переходят в кривые. Такой же плавный переход может быть между прямыми или между двумя окружностями.
Плавный переход одной линии в другую называют сопряжением.
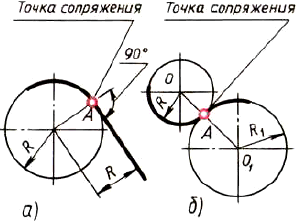Рис. 131. Построение сопряжений
Рис. 132. Общий способ построения сопряжений двух пересекающихся прямых
Для всех трех случаев применяют общий способ построения.
Сопряжение окружности и прямой дугой заданного радиуса. Даны окружность радиуса R, отрезок АВ и радиус дуги сопряжения R1 (рис. 133).
Рис. 133. Построение сопряжения дуги окружности и прямой
|
Рис. 66. Сопряжение двух параллельных прямых
Проведение касательной к окружности. Задана окружность с центром О и точка А (рис. 67, а). Требуется провести из точки А касательную к окружности.
1. Точку А соединяют прямой с заданным центром О окружности.
Строят вспомогательную окружность диаметром, равным ОА (рис. 67, а). Чтобы найти центр О1 делят отрезок ОА пополам (см. рис. 56).
2. Точки m и n пересечения вспомогательной окружности с заданной - искомые точки касания. Точку А соединяют прямой с точками m или n (рис. 67, б). Прямая Am будет перпендикулярна к прямой Оm, так как угол АmО опирается на диаметр.
Рис. 67. Построение касательной к двум окружностям
Проведение прямой, касательной к двум окружностям. Заданы две окружности радиусом R и R1. Требуется построить касательную к ним.
Различают два случая касания: внешнее (рис. 68, б) и внутреннее (рис. 68, в).
При внешнем касании построение выполняют следующим образом:
1. Из центра О проводят вспомогательную окружность радиусом, равным разности радиусов заданных окружностей, т. е. R - R1 (рис. 68, а). К этой окружности из центра О1 проводят касательную Оm. Построение касательной показано на рис. 67.
2. Радиус, проведенный из точки О в точку n, продолжают до пересечения в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm проводят радиус 01р меньшей окружности. Прямая, соединяющая точки сопряжений m и р,- касательная к заданным окружностям (рис. 68, б).
При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R1 (см. рис. 68, в). Затем из центра O1 проводят касательную к вспомогательной окружности (см. рис. 67). Точку n соединяют радиусом с центром О. Параллельно радиусу On проводят радиус O1р меньшей окружности. Искомая касательная проходит через точки сопряжений m и р.
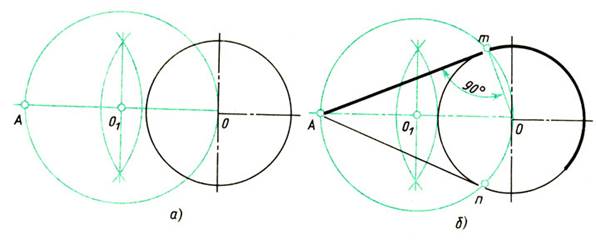
Рис. 68. Построение касательной к окружности
Сопряжение дуги и прямой линии дугой заданного радиуса. Заданы дуга окружности радиусом R и прямая. Требуется соединить их дугой радиусом R1.
1. Находят центр сопряжения (рис. 69, а), который должен находиться на расстоянии R1 от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R1, и вспомогательной дуги, отстоящей от заданной также на расстоянии R1. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R1 (рис. 69, а). Раствором циркуля, равным сумме заданных радиусов R + R1, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O1- центр сопряжения.
2. По общему правилу находят точки сопряжения (рис. 69, б). Соединяют прямой центры сопрягаемых дуг O1 и О. Опускают из центра сопряжения O1 перпендикуляр на заданную прямую.
3. Из центра сопряжения O1 между точками сопряжения m и n проводят дугу, радиус которой равен R1 (см. рис. 69, б).
Сопряжение двух дуг окружности дугой заданного радиуса. Заданы две дуги радиусами R1 и R2. Требуется построить сопряжение дугой, радиус которой задан.
Различают два случая касания: внешнее (рис. 70, б) и внутреннее (рис. 70, в). В обоих случаях центры сопряжений должны быгь расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.
Ниже приведен порядок построения для внешнего и внутреннего касаний.
Для внешнего касания. 1. Из центров O1 и О2 раствором циркуля, равным сумме радиусов заданной и сопрягающей дуг, проводят вспомогательные дуги (рис. 70, а); радиус дуги, проведенной из центра O1, равен R + R3, а радиус дуги, проведенной из центра O2, равен R2 + R3. На пересечении вспомогательных дуг расположен центр сопряжения - точка О3,.
2. Соединив прямыми точку O1 с точкой O3 и точку O2 с точкой O3, находят точки сопряжения m и n (см. рис. 70, б),
3. Из точки О3 раствором циркуля, равным R3, между точками m и n описывают сопрягающую дугу.
Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R4-R1 и R4-R2. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О4 с точками O1 и O2.
Рис. 70. Сопряжение двух дуг окружности
Выполнить лист 2 в ДКР по теме: Геометрические построения согласно своему варианту смотри приложение № 2
